この記事では、観測値が1次元の場合の線形カルマンフィルタのアルゴリズムについて解説し、マイコン等でセンサの計測値を補正する際の実装方法についてシミュレーションを行う。
観測値が1次元である場合、逆行列の計算が不要となるため、マイコン等への実装が簡単になる。
そして距離・温度・気圧など、主要なセンサにより取得できる計測値は1次元であることから、1次元カルマンフィルタは機械設計における基盤的な手法となりうる。
今回は距離センサの測定値補正に注目し、Python言語によるシミュレーションを実施する。
以上より、この記事を読むことでセンサ補正機能の実装方法と考え方を理解することができる。
カルマンフィルタ
文字の意味
- \(\mathbf{x}\) :状態ベクトル
- \(\mathbf{P}\) :状態ベクトルの誤差共分散行列
- \(y\) :観測値(1次元)
- \(u\) :制御入力(1次元)
- \(\mathbf{g}\) :カルマンゲイン
これらを離散時間 \(k\) の関数として扱い、 \(\mathbf{x}(k)\) のように表記する。
また、ハット( \(\hat{\mathbf{x}}\) )はそれぞれの推定値を表し、上付きのマイナスは( \(\mathbf{P}^-\) )それぞれの事前値(予測ステップ[後述]での値)を表す。
カルマンフィルタが行うこと
過去の情報と観測値に基づいて、状態ベクトルを適切に推定する(適切な \(\hat{\mathbf{x}}\) を求める)。
具体的には、
予測ステップで状態ベクトルの事前推定値 \(\hat{\mathbf{x}}^-\) と事前誤差共分散行列 \(\mathbf{P}^-\) を計算し、
フィルタリングステップで観測値に基づいて事前値を修正して、状態ベクトルの推定値( \(\hat{\mathbf{x}}\) )と誤差共分散行列( \(\mathbf{P}\) )を求める。
状態空間モデル
前提として、状態ベクトル・観測値・制御入力の間には、行列 \(\mathbf{A}\) とベクトル \(\mathbf{b}, \mathbf{b}_u, \mathbf{c}\) を用いて、以下の関係式が成り立っているとする。
$$\mathbf{x}(k+1)=\mathbf{Ax}(k)+\mathbf{b}_u u(k)+\mathbf{b}v(k)$$
$$y(k)=\mathbf{c}^\mathrm{T}\mathbf{x}+w(k)$$
ここで、 \(v\) はシステム雑音(状態ベクトルを更新する際に生じる雑音)、 \(w\) は観測雑音(状態ベクトルを観測値に変換する際に生じる雑音)である。
それぞれ、平均が \(0\) 、分散が \(\sigma_v^2, \sigma_w^2\) の正規分布にしたがう雑音である。
初期値
状態ベクトルの推定値と誤差共分散行列の初期値を以下のように定義して、カルマンフィルタによる更新を開始する。
$$\hat{\mathbf{x}}(0)=\mathrm{E}[\mathbf{x}(0)]$$
$$\mathbf{P}(0)=\mathrm{E}\left[(\mathbf{x}(0)-\mathrm{E}[\mathbf{x}(0)])(\mathbf{x}(0)-\mathrm{E}[\mathbf{x}(0)])^\mathrm{T}\right]$$
すなわち、状態ベクトルの正規性を仮定している。
更新式
\(k=1,2,\cdots\) について、以下の2段階で値の更新を行う。
予測ステップ
- 状態ベクトルの事前推定値
$$\hat{\mathbf{x}}^-(k)=\mathbf{A}\hat{\mathbf{x}}(k-1)+\mathbf{b}_u u(k-1)$$
- 事前誤差共分散行列
$$\mathbf{P}^-(k)=\mathbf{AP}(k-1)\mathbf{A}^\mathrm{T}+\sigma_v^2\mathbf{bb}^\mathrm{T}$$
フィルタリングステップ
- カルマンゲイン
$$\mathbf{g}(k)=\frac{\mathbf{P}^-(k)\mathbf{c}}{\mathbf{c}^\mathrm{T}\mathbf{P}^-(k)\mathbf{c}+\sigma_w^2}$$
- 状態ベクトルの推定値
$$\hat{\mathbf{x}}(k)=\hat{\mathbf{x}}^-(k)+\mathbf{g}(k)\left(y(k)-\mathbf{c}^\mathrm{T}\hat{\mathbf{x}}^-(k)\right)$$
- (事後)誤差共分散行列
$$\mathbf{P}(k)=(\mathbf{I}-\mathbf{g}(k)\mathbf{c}^\mathrm{T})\mathbf{P}^-(k)$$
実装例:Pythonによるシミュレーション
設定
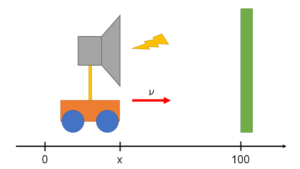
ここでは、あまり精度が良くない超音波測距センサを取り付けた車を例に、カルマンフィルタの実装例を示す。
センサの精度がどのくらい精度が良くないのかというと、
- 観測誤差 \(\sigma_w^2=16\) (m)。すなわち、観測値が真値から \(\pm 2\sigma_w=8\) (m)程度ずれる
- \(p=0.05\) の確率で、車の位置によらず、観測値が \(0\) になる
というものである。
なお、車の初期位置 \(x=0\) の \(100\) (m)前方には壁があり、測距センサは車とこの壁の間の距離を出力する。
また、センサを含めた車の質量を \(m=1\) (kg)とする。
すなわち、車に加える制御入力を \(u\) (N)、車の加速度を \(a\) (m/s^2)とすると、運動方程式より
$$u=a$$
が成り立つ。
\(u\) は離散時間 \(k\) の関数とし、
$$u(k)=500\cos\left(\frac{\pi k}{50}\right)$$
と変化させる。
車の位置と速度をそれぞれ \(x\) (m), \(\nu\) (m/s)、時間ステップの間隔を \(\Delta t\) (s)、測距センサの測定値を \(100-y\) (m)とすると、このシステムの状態方程式は以下のように書ける。
$$\begin{bmatrix} x(k+1) \\ \nu(k+1) \end{bmatrix}=\begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix}\begin{bmatrix} x(k) \\ \nu(k) \end{bmatrix}+\begin{bmatrix} 0 \\ \Delta t \end{bmatrix}u(k)+\begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix}v(k)$$
$$y(k)=\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix} x(k) \\ \nu(k) \end{bmatrix}+w(k)$$
ここで、位置と速度には同等のシステムノイズ( \(\sigma_v=0.1\) )が乗るものと仮定した。
また、測距センサの設定より、観測ノイズの標準偏差は \(\sigma_w=4\) である。
位置と速度を状態ベクトル \(\mathbf{x}\) としてまとめ、 \(\Delta t=0.01\) とすると、
$$\mathbf{A}=\begin{bmatrix} 1 & 0.01 \\ 0 & 1 \end{bmatrix}, \mathbf{b}_u=\begin{bmatrix} 0 \\ 1 \end{bmatrix}$$
$$\mathbf{b}=\begin{bmatrix} 0.1 \\ 0.1 \end{bmatrix}, \mathbf{c}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}$$
とおける。
実装例
以上の設定をPythonで実装すると以下のNotebookのようになる。
ここでは、車のクラス[2]とその更新関数[3]、さらにカルマンフィルタ[4]の関数を定義し、 \(\sigma_v=0.1\) のときの真値と測定値[7]、さらに真値とカルマンフィルタによる推定値[8]を比較している。
\(\sigma_v=0.01\) とし、システムノイズを小さくすると[9]、真値と推定値の差が小さくなっていることがわかる[11]。

Comments