「ロジスティック方程式」と「ロジスティックシグモイド関数」の関係についての考察

Index

動機
考察
まとめ

動機

ロジスティックシグモイド関数

$$p=\frac{1}{1+e^{-a}}\tag{1}$$

は、$p$ を確率値として見た時の対数オッズ（ロジット関数）

$$a=\ln{\frac{p}{1-p}}\tag{2}$$

の逆関数として導出される。すなわち、対数オッズの値から確率を計算する関数である。このような性質から、ロジスティック回帰分析などの機械学習の分野でよく利用されている。

しかし、この関数について、生物個体数の時間変化を表したロジスティック方程式

$$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)\tag{3}$$

の解

$$N=\frac{N_{0}Ke^{rt}}{K-N_{0}+N_{0}e^{rt}}\tag{4}$$

において $K=1$, $N_{0}=0.5$, $r=1$ と置くことによっても、同じ形

$$N=\frac{1}{1+e^{-t}}\tag{5}$$

が得られる。（ロジスティック方程式と解の導出、後に登場するマルサス係数 $m$ については

を参照のこと）

一方は確率と対数オッズの関係からの式変形であり、もう一方は生物モデルの結論という、一見関係なさそうなものが同じ結果を導いているのは不思議である。

この記事では、以上のように確率的観点（ロジット関数）と生物学的観点（ロジスティック方程式）の双方から、同じ形の関数が得られる理由について考察する。

考察

結論

結論を先に示すと、以下の操作がロジスティックシグモイド関数を導いていると考えられる。

$K=1$, $N_{0}=0.5$, $r=1$ という代入
マルサス係数 $m$ が線形に減少するという仮定

以下、ロジスティック方程式とロジット関数の双方から議論を進め、結果的に同じ内容を導いていることを示す。

ロジスティック方程式から

ロジスティック方程式の変数の意味を考えながら、結論 1. のルールに沿って値を順次代入していく。

まず、環境収容力 $K$ は個体数 $N$ の最大値である。$K=1$ と置くと、$N$ が非負であることと合わせて $0\leq N\leq 1$ が導かれ、この時点で $N$ が確率 $p$ と同様の定義域を持つことがわかる。

次に、個体数の初期値 $N_{0}$ は $t=0$ の時の $N_{0}$ の値であることに注目する。式 $(1), (5)$ を比較するとわかる通り、$p\leftrightarrow N$, $a\leftrightarrow t$ の対応関係があり、$N_{0}=0.5$ という値は $N$ を確率、$t$ を対数オッズと見た時に

$$t=\ln{\frac{N}{1-N}}=\ln{\frac{0.5}{1-0.5}}=0$$

が矛盾なく成立するように設定されている。

以上の通り、$K$, $N_{0}$ に対する値の代入は、$p\leftarrow N$, $a\leftarrow t$ の変換が矛盾なく行われるよう、意図されたものであると考えることができる。

ロジット関数から

ここで一度ロジスティック方程式を離れ、確率的観点から話を進める。対数オッズ $a$ と確率 $p$ の増加量の関係について考えるために、まず

$$b=\ln{p}$$

という、確率の対数 $b$ と確率 $p$ の関係について見ていく。上式から

$$p=\exp(b)$$

であり、これを $b$ で微分すると

$$\frac{dp}{db}=\exp(b)=p$$

が得られる。すなわち、$b$ が増加した時の $p$ の増分は、$p$ 自身の値に等しい（比例する）。マルサス係数的に $m$ を持ち出せば

$$\frac{dp}{db}=mp\quad(m=1)\tag{6}$$

である。これを踏まえてロジット関数 $(2)$ について考える。

$a$ が増加した時の $p$ の増分について考えた時、式 $(6)$ のように $m=1$ となるだろうか？答えは否である。なぜならば、$a$ が増加した時のことを考えると

$$a\uparrow=\ln{\frac{p\uparrow}{(1-p)\downarrow}}$$

のように、分子・分母の増減は連動しているため、$a$ の増加は $p$ の増加と $1-p$ の減少の双方に起因している（逆に言えば、$a$ の増加による影響は、$p$ と $1-p$ で”分割”される）ことがわかる。そのため、$p$ の増え方は式 $(6)$ の時よりも小さく、$m<1$ となるはずである。

では、実際にはどのくらい小さくなるのだろうか？それを確かめるためには、ロジット関数 $(2)$ を微分してみればよい。

$$\frac{da}{dp}=\frac{1}{p}+\frac{1}{1-p}=\frac{1}{p(1-p)}$$

より

$$\frac{dp}{da}=\frac{1}{\frac{da}{dp}}=p(1-p)$$

であり、式 $(6)$ と比較すると $m=1-p$ 、すなわち、$m$ は $p$ の値に対して「線形に減少させればよい」。この結果は、結論 2. の操作と一致する。

また、内的自然増加率 $r$ は $m$ の最大値であり、$r=1$ であることが自然に導かれる。

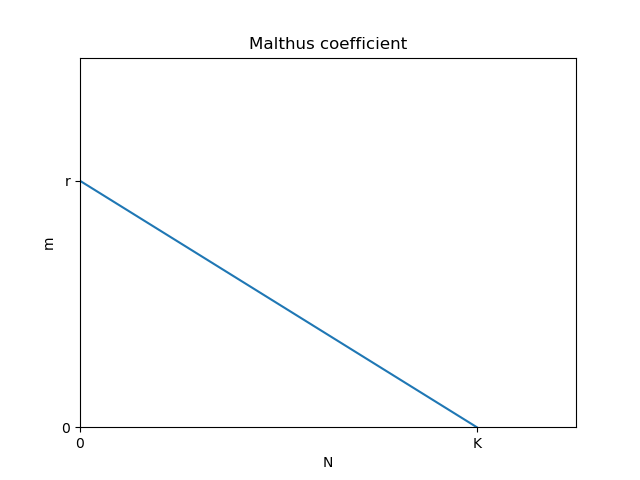
したがって、確率的観点（ロジット関数）と生物学的観点（ロジスティック方程式）は、結論 1. 2. の操作を通して相互に結びついていることが示された。

まとめ

確率的観点（ロジット関数）においては、対数オッズ $a$ の増加に対して $p$ が増えすぎないような線形の制約が内在しており、生物学的観点（ロジスティック方程式）においては、変数を確率として矛盾なく読み替えられるよう値を代入することができる。以上の結果が、ロジスティックシグモイド関数という共通の結果を導いたと考えられる。

動機

考察

結論

ロジスティック方程式から

ロジット関数から

まとめ

Comments