半加算器（1bit加算器）の回路図と動作原理

Index

概要

「半加算器とは何か？」

半加算器を構成する回路図を読み解いて、その動作原理を解説する。

この記事を読むことで、NOT/OR/ANDの論理回路を組み合わせて足し算を行う基本的な方法について理解できる。

この記事はシリーズ「半導体からコンピュータを作る」の第８章である。

過去の章で前提となる知識を解説しているため、不明点があれば参照してほしい。

また、記事の内容を理解した後、シリーズの他の記事を読み進めることで、半導体やコンピュータに関する知識を深めることができる。

1bitは０と１を表現できるため、1bitどうしの加算には以下の４パターンがある。

ここで、数字を電気回路で表現するために、0 = L, 1 = Hと考える。

上記のような1bitの足し算を行う回路を半加算器という。

この回路はNOT・OR・ANDの論理回路を組み合わせて作ることができる。

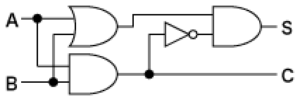
上の回路図において、Aは入力１、Bは入力２である。

また、Sは出力（Sum）、Cは桁上げ出力（Carry out）と呼ばれる。

つまりSが一の位、Cが二の位を表す。

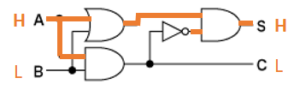
上図のオレンジの線がHの領域である。

これは、２進数の計算 1 + 0 = 01 の例である。

入力１（A）	入力２（B）	桁上げ出力（C）	出力（S）
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

真理値表より、1bitどうしの４パターンの加算すべてを表現できていることがわかる。

半加算器（とORゲート）を組み合わせて、任意の桁の足し算を行う全加算器を作る。

全加算器の回路図を解析し、その動作原理を解説する。