概要
この記事では、ミルマンの定理について説明した後、その証明を行う。
また、別記事にて定理の公式から、等価回路を考える上での示唆を考察する。
定理
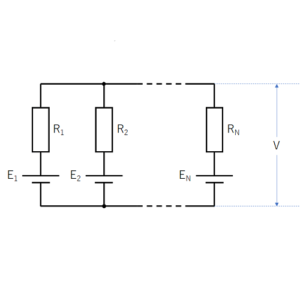
図1
図1のように、 \(N\) 個の枝路に電源と抵抗が並列に接続されている回路を考える。(この回路は、内部抵抗を持つ電池の並列接続と考えることができる)
ここで、それぞれの電源電圧を \(E_1,E_2,\ldots,E_N\) 、抵抗値を \(R_1,R_2,\ldots,R_N\) とする。
このとき、図1の \(V\) で示した部分の電圧は
$$V=\frac{\frac{E_1}{R_1}+\frac{E_2}{R_2}+\cdots+\frac{E_N}{R_N}}{\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_N}}$$
となる。
電源が逆向きに接続されている場合は、対応する分子の符号を負にする。
証明
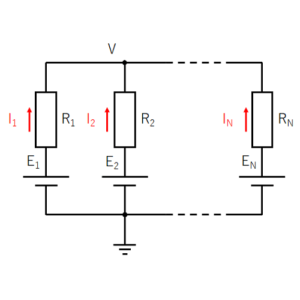
図2
図2のように、各抵抗を流れる電流値を \(I_1,I_2,\ldots,I_N\) とおくと
$$I_1+I_2+\cdots+I_N=0\tag{1}$$
となる。
また、電源の負極側を設置して、各導線における電位を考えると、各枝路において
$$E_1-R_1I_1=V\Leftrightarrow I_1=\frac{E_1-V}{R_1}$$
$$E_2-R_2I_2=V\Leftrightarrow I_2=\frac{E_2-V}{R_2}$$
$$\vdots$$
$$E_N-R_NI_N=V\Leftrightarrow I_N=\frac{E_N-V}{R_N}$$
が成り立ち、これらを式 \((1)\) に代入すると
$$\frac{E_1-V}{R_1}+\frac{E_2-V}{R_2}+\cdots+\frac{E_N-V}{R_N}=0$$
$$V\left(\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_N}\right)=\frac{E_1}{R_1}+\frac{E_2}{R_2}+\cdots+\frac{E_N}{R_N}$$
$$V=\frac{\frac{E_1}{R_1}+\frac{E_2}{R_2}+\cdots+\frac{E_N}{R_N}}{\frac{1}{R_1}+\frac{1}{R_2}+\cdots+\frac{1}{R_N}}$$
が導かれる。

Comments