RLCバンドパスフィルタのシミュレーション

Index

概要
直列RLCバンドパスフィルタ
微分方程式からシミュレーションを行う
Pythonによる実装

概要

この記事では、直列RLCバンドパスフィルタを例に、アナログフィルタ回路のシミュレーションを行う方法について解説する。

今回はPython言語を用いて、350Hz付近の周波数を持つ波形を選択的に通過させるフィルタに対し、350Hz、10,000Hz、50Hzの波を入力した際の出力を描画することを目標にする。

この記事を読むことで、コイルやコンデンサを含み、全体の挙動が微分方程式で表されるような電子回路について、LTSpiceのようなシミュレーションを１から実装して動作を検証できるようになる。

直列RLCバンドパスフィルタ

回路図

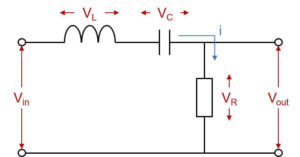
本記事では、コイル・コンデンサ・抵抗を直列に接続した直列RLCバンドパスフィルタを取り扱う。

この回路により、 $V_{in}$ として入力した電圧のうち、特定の周波数帯域の成分のみを $V_{out}$ として取り出すことができる。

パラメータ

今回は、コイルのインダクタンス $L$ 、コンデンサのキャパシタンス $C$ 、抵抗値 $R$ を以下のように設定した。

$L=1\mathrm{mH}$
$C=200\mathrm{\mu F}$
$R=10\mathrm{\Omega}$

フィルタの性質

直列RLCバンドパスフィルタの中心周波数 $f_0$ 、低周波側カットオフ周波数 $f_{CL}$ 、高周波側カットオフ周波数 $f_{CH}$ は以下の式で求められる。

中心周波数： $f_0=\frac{1}{2\pi\sqrt{LC}}$
低周波側カットオフ周波数： $f_{CL}=\frac{1}{2\pi RC}$
高周波側カットオフ周波数： $f_{CH}=\frac{R}{2\pi L}$

なお、カットオフ周波数は $3\mathrm{dB}$ の減衰が得られる周波数として定義される。

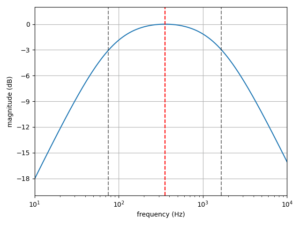
前節で設定したパラメータから計算すると

$f_0=\frac{1}{2\pi\sqrt{10^{-3}\cdot 2\cdot10^{-4}}}\simeq 356\mathrm{Hz}$
$f_{CL}=\frac{1}{2\pi\cdot 10\cdot 2\cdot 10^{-4}}\simeq 80\mathrm{Hz}$
$f_{CH}=\frac{10}{2\pi\cdot 10^{-3}}\simeq 1592\mathrm{Hz}$

となり、 $V_{in}$ として入力した周波数ごとの、$V_{out}$ で得られるゲインの変化を図示すると以下のようになる。

微分方程式からシミュレーションを行う

直列RLCバンドパスフィルタの微分方程式

回路図より、電圧について以下の関係式が成り立つ。

$$V_{in}=V_L+V_C+V_R$$

右辺の電圧を、回路を流れる電流 $i$ を用いてそれぞれ表現すると

$$V_{in}=L\frac{di}{dt}+\frac{1}{C}\int i dt+Ri$$

という微分方程式が得られる。

微分方程式の離散化

ここで、 $I_c=\int i dt$ とおき、微分方程式を離散化すると

$$V_{in}(t)=L\frac{\Delta i(t)}{\Delta t}+\frac{1}{C}I_c(t)+Ri(t)$$

となる。ここで、離散化に基づく以下の関係式

$$i(t)=i(t-1)+\frac{\Delta i(t)}{\Delta t}\Delta t\tag{1}$$

$$I_c(t)=I_c(t-1)+i(t)\Delta t=I_c(t-1)+\left\{i(t-1)+\frac{\Delta i(t)}{\Delta t}\Delta t\right\}\Delta t\tag{2}$$

を適用し、 $\frac{\Delta i(t)}{\Delta t}$ について解くと

$$V_{in}(t)=L\frac{\Delta i(t)}{\Delta t}+\frac{1}{C}\left[I_c(t-1)+\left\{i(t-1)+\frac{\Delta i(t)}{\Delta t}\Delta t\right\}\Delta t\right]+R\left\{i(t-1)+\frac{\Delta i(t)}{\Delta t}\Delta t\right\}$$

$$\left\{L+\frac{(\Delta t)^2}{C}+R\Delta t\right\}\frac{\Delta i(t)}{\Delta t}=V_{in}(t)-\frac{I_c(t-1)+i(t-1)\Delta t}{C}-Ri(t-1)$$

$$\frac{\Delta i(t)}{\Delta t}=\frac{V_{in}(t)-\frac{I_c(t-1)+i(t-1)\Delta t}{C}-Ri(t-1)}{L+\frac{(\Delta t)^2}{C}+R\Delta t}\tag{3}$$

となる。

シミュレーションの流れ

前節で微分方程式を $\frac{\Delta i(t)}{\Delta t}$ について解いたのは、 $I_c(t)$ や $i(t)$ に比べ、 $\frac{\Delta i(t)}{\Delta t}$ の $V_{in}(t)$ に対する反応が最も速いためである。

具体的には、例えば $V_{in}$ が変化したからといってコンデンサに蓄えられている電荷（ $I_c$ ）が急激に変化することは考えにくい。

そして、そもそも $I_c(t)$ や $i(t)$ は式 $(1), (2)$ を通して $\frac{\Delta i(t)}{\Delta t}$ によってその変化量が制御されている。

したがって、フィルタ回路のシミュレーションは以下の手順で実施する。

$I_c(t-1), i(t-1)$ を用い、式 $(3)$ にしたがって、回路の微分方程式をみたす $\frac{\Delta i(t)}{\Delta t}$ の値をもとめる。
$i(t)=i(t-1)+\frac{\Delta i(t)}{\Delta t}\Delta t$ により $i$ を更新する。
$I_c(t)=I_c(t-1)+i(t)\Delta t$ により $I_c$ を更新する。

なお、フィルタ回路の出力端子と抵抗は並列関係にあるので、出力電圧は

$$V_out(t)=V_R(t)=Ri(t)$$

として求めることができる。

Pythonによる実装

シミュレーションでは、サンプリングレートを10,000Hz（10,000フレームで1秒）とし、200フレーム分の電圧波形を直列RLCバンドパスフィルタに入力した。

import numpy as np
from matplotlib import pyplot as plt

def simulate(v, sample=10000, R=10, L=10**-3, C=2*10**-4):
    step = len(v)
    dt = 1 / sample
    save = np.zeros(step)
    i = 0
    Ic = 0
    for t in range(step):
        didt = (v[t] - R*i - (Ic+i*dt)/C) / (L + dt*dt/C + R*dt)
        i += didt * dt
        Ic += i * dt
        save[t] = R*i
    return save

step = 200

v350 = simulate(np.array([np.sin(t*2*np.pi*0.035) for t in range(step)])) # 350Hz
v10000 = simulate(np.array([np.sin(t*2*np.pi*1) for t in range(step)])) # 10000Hz
v50 = simulate(np.array([np.sin(t*2*np.pi*0.005) for t in range(step)])) # 50Hz

plt.plot(v350, label="350Hz")
plt.plot(v10000, label="10,000Hz")
plt.plot(v50, label="50Hz")
plt.legend()
plt.xlabel("time (sec)")
plt.ylabel("Vout")
plt.xticks([50*i for i in range(5)], [50*i/10000 for i in range(5)])
plt.tight_layout()
plt.savefig("Vout.png")

入力したのは振幅が1で周波数がそれぞれ350Hz, 10,000Hz, 50Hzのsin波であり、それぞれに対する出力を描画した。

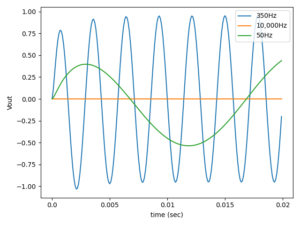
その結果、中心周波数に近い350Hzの波はほとんどロスなく伝達されたのに対し、カットオフ周波数から遠く離れた10,000Hzの波は大きく減衰した。