デルタ関数は条件分岐や積分で活躍する便利な関数です。
ここではクロネッカーのデルタ・ディラックのデルタ関数を定義し、それらが持つ性質を網羅的に解説します。
この記事を読むことで、クロネッカーのデルタ・ディラックのデルタ関数のイメージを掴み、数式上でif文やパルスを表現することができるようになります。
クロネッカーのデルタ
定義
クロネッカーのデルタは、離散的な変数(整数の集合など) \(i,j\) に対して、以下のように定義される。
$$\delta_{ij}=\begin{cases}1\quad(i=j) \\ 0\quad(i\neq j)\end{cases}$$
また、
$$\delta_{ij}=\delta(i, j)$$
と表記することもある。
定義の拡張
定義により、クロネッカーのデルタは以下の性質を持ちます。
- $$\sum_{j}\delta_{ij}a_j=a_i$$
- $$\sum_{i}a_i\delta_{ij}=a_j$$
- $$\sum_{k}\delta_{ik}\delta_{kj}=\delta_{ij}$$
関数のイメージ
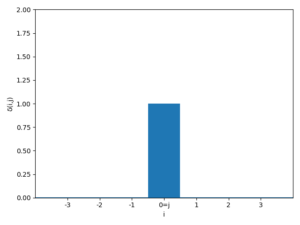
定義からもわかる通り、 \(i\) の値が \(j\) となるときのみ1(True)、それ以外は0(False)になります。
すなわち、クロネッカーのデルタは、条件分岐を数式上で表現できる関数なのです。
例えば、
A = [(0, 1), (1, 2), (2, 3), (0, 4), (1, 5), (2, 6)]
c = sum([a[1] if a[0] == 1 else 0 for a in A])
print(c) # 7 = 0 + 2 + 0 + 0 + 5 + 0のような、特定の条件を満たす場合のみ加算し、それ以外は無視するといったような計算を表現することができます。
例
$$a_0=0,\quad a_1=1,\quad a_2=2,\quad a_3=0,\quad a_4=1,\quad a_5=2$$
$$b_0=1,\quad b_1=2,\quad b_2=3,\quad b_3=4,\quad b_4=5,\quad b_5=6$$
のとき
$$c=\sum_{n=0}^{5}\delta(1,a_n)b_n$$
とおくと
$$c=0+2+0+0+5+0=7$$
より、前述のPythonコードを数式で表現できます。
ディラックのデルタ関数
定義
クロネッカーのデルタが離散的な変数に対して用いられるのに対し、
これを連続変数に対して拡張したものがディラックのデルタ関数です。
ディラックのデルタ関数について、以下に2通りの定義を示します。
定義その1(難しい)
任意の実連続関数 \(f:\mathbf{R}\to\mathbf{R}\) に対し
$$\int_{-\infty}^{\infty}f(x)\delta(x)dx=f(0)$$
をみたす実数値シュワルツ超関数 \(\delta\) のことをディラックのデルタ関数という。
定義その2(簡単)
ディラックのデルタ関数 \(\delta(x)\) は以下を満たす。
- $$\delta(x)=\begin{cases}\infty\quad(x=0) \\ 0\quad(x\neq 0)\end{cases}$$
- $$\int_{-\infty}^{\infty}\delta(x)dx=1$$
実用上は定義その2の理解で問題ありません。
関数のイメージ
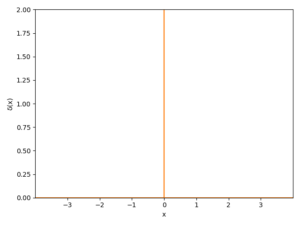
定義その2より、ディラックのデルタ関数は \(x=0\) のときに \(\infty\) となり、それ以外の \(x\) ではすべて \(0\) である特殊な関数です。
そして、全区間を積分すると \(1\) になります。
クロネッカーのデルタとの関係

次に、デルタ関数どうしの関係を考えます。
クロネッカーのデルタは整数の関数なので、ゼロでない値は整数1個分の幅(図では \(-0.5\) と \(0.5\) の間)に存在すると考えることができます。
よって底辺=1、また、この値が1なので高さ=1とします。
以上より、図中央の四角形の面積は1であり、その他の値は0なので、ディラックのデルタの全区間での積分も1となります。
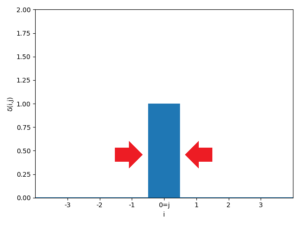
この面積を保ったまま、図中央の四角形を左右から押しつぶすことを考えます。
その結果、底辺 \(\rightarrow 0\) となるのに合わせて、高さ \(\rightarrow \infty\)となります。
よって
$$δ(0)=1$$
と考えることができるのです。
性質とその解説
前節で図を用いて示した通り、ディラックのデルタ関数は、離散変数で定義されるクロネッカーのデルタ
$$\sum_{i=-\infty}^{\infty}f_i\delta_{ij}=f_j$$
の、連続変数への自然な拡張になっています。
また、ディラックのデルタ関数は以下の性質を持ちます。
- $$\int_{-\infty}^{\infty}f(x)\delta(x-a)dx=f(a)$$
- $$\delta(-x)=\delta(x)$$
- $$\delta(x)=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}e^{inx}$$
- $$\delta(ax)=\frac{1}{a}\delta(x)\quad(a> 0)$$
性質1.の解説
性質 1. は特に無限積分である必要はありません。
積分区間 \([\alpha,\beta]\) が \(\alpha< a< \beta\) のように \(a\) を含んでいるならば、
$$\int_{\alpha}^{\beta}f(x)\delta(x-a)dx=f(a)$$
となり、
\(f(x)\) に \(\delta(x-a)\) を掛けて \(a\) を含む区間で積分すると、 \(f(a)\) の値のみを抽出することができます。
性質2.の解説
ディラックのデルタ関数は偶関数です。
性質3.の解説
この式はディラックのデルタ関数の複素形フーリエ級数による展開を示したものです。

複素形フーリエ級数で展開できるのは周期関数に限られるため、まず、
$$\delta(x-2k\pi)=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}e^{inx}$$
を考えます。このとき、
$$\delta(x-2k\pi)=\begin{cases} \infty\quad(x=2k\pi) \\ 0\quad(x\neq 2k\pi)\end{cases}\quad(k=0,1,2,\cdots)$$
であり、すなわち周期 \(2\pi\) で値が \(\infty\) となる関数を考えています。
ここで、この関数の定義域を \([-\pi,\pi]\) に絞ることによって、左辺はディラックのデルタ関数に等しくなります。
したがって、
$$\delta(x-2k\pi)=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}c_n e^{inx}$$
です。この式の係数は
$$c_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}\delta(x)e^{-inx}dx$$
より求められ、 \(f(x)=e^{-inx}\) とおくと \(f(0)=e^0=1\) なので
$$c_n=\frac{1}{2\pi}f(0)=\frac{1}{2\pi}$$
となります。
したがって、任意の整数 \(n\) について \(c_n=\frac{1}{2\pi}\) より、
$$\delta(x)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\delta(x)f(x)dx=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty}e^{inx}$$
が成り立ちます。
性質4.の解説
\(ax=t\)とおくと、
$$\frac{d(ax)}{dt}=\frac{dt}{dt}$$
$$a\frac{dx}{dt}=1$$
$$adx=dt$$
より、
$$\delta(x)dx=\delta(t)dt=\delta(ax)adx$$
したがって、
$$\delta(ax)=\frac{1}{a}\delta(x)$$
が成り立ちます。


Comments