超幾何分布の効率的数値計算法

概要

超幾何分布の確率質量関数は

$$P(x|N,K,n)=\frac{\binom{K}{x}\binom{N-K}{n-x}}{\binom{N}{n}}$$

であり、これをすべての \(x\) について計算することによって累積分布関数を求めることができる（一般超幾何関数を用いた一般形による表記法は省略）。

しかし、式の中に二項係数・順列の計算が多く、計算機上での実行に時間がかかることも少なくない。

この記事では、漸化式の考え方を用いて、効率的に超幾何関数の確率質量関数・累積分布関数の効率的な数値計算法を提案する。

最後に、Pythonを用いた精度検証実験も行う。

数値計算法

$$a(x)=P(x|N,K,n)$$

とおくと、この数列の初項 \(a(0)\) は

$$a(0)=\begin{cases}\frac{(N-K)(N-K-1)\cdots(N-K-n+1)}{N(N-1)\cdots(N-n+1)}&&(n\leq K) \\ \frac{(N-n)(N-n-1)\cdots(N-n-K+1)}{N(N-1)\cdots(N-K+1)}&&(n>K)\end{cases}$$

となる。ここから、漸化式

$$a(x+1)=\frac{(K-x)(n-x)}{(x+1)(N-K-n+x+1)}a(x)$$

を順次用いて任意の確率質量関数の値を求める。

導出

初項について

$$a(0)=P(0|N,K,n)$$

$$=\frac{\binom{K}{0}\binom{N-K}{n}}{\binom{N}{n}}$$

$$=\frac{(N-K)!n!(N-n)!}{n!(N-K-n)!N!}$$

$$=\frac{(N-K)!(N-n)!}{(N-K-n)!N!}\tag{1}$$

$$=\frac{(N-K)!}{(N-K-n)!}\frac{(N-n)!}{N!}$$

$$=\frac{(N-K)(N-K-1)\cdots(N-K-n+1)}{N(N-1)\cdots(N-n+1)}\tag{2}$$

となる。また、式 \((1)\) からは

$$=\frac{(N-K)!}{N!}\frac{(N-n)!}{(N-K-n)!}$$

$$=\frac{(N-n)(N-n-1)\cdots(N-n-K+1)}{N(N-1)\cdots(N-K+1)}\tag{3}$$

という変形もできる。

このとき、式 \((2),(3)\) の分子分母にはそれぞれ \(n, K\) 個の因数が存在する。

したがって、計算量を減らすためには

$$a(0)=\begin{cases}\frac{(N-K)(N-K-1)\cdots(N-K-n+1)}{N(N-1)\cdots(N-n+1)}&&(n\leq K) \\ \frac{(N-n)(N-n-1)\cdots(N-n-K+1)}{N(N-1)\cdots(N-K+1)}&&(n>K)\end{cases}$$

を選択すればよい。

また、

$$a(x)=\frac{K!(N-K)!n!(N-n)!}{x!(K-x)!(n-x)!(N-K-n+x)!N!}$$

$$a(x+1)=\frac{K!(N-K)!n!(N-n)!}{(x+1)!(K-x-1)!(n-x-1)!(N-K-n+x+1)!N!}$$

より、

$$\frac{a(x+1)}{a(x)}=\frac{(K-x)(n-x)}{(x+1)(N-K-n+x+1)}$$

$$a(x+1)=\frac{(K-x)(n-x)}{(x+1)(N-K-n+x+1)}a(x)$$

として、漸化式が求まる。

実験

\(N=100, K=30, n=50\) として、scipyの組み込み関数との比較を行った。

import numpy as np
from scipy.stats import hypergeom

N = 100
K = 30
n = 50

if n <= K:
    pmf = [np.prod([(N-K-i) / (N-i) for i in range(n)])]
else:
    pmf = [np.prod([(N-n-i) / (N-i) for i in range(K)])]
for i in range(K):
    pmf.append(pmf[i] * (K-i) * (n-i) / ((i+1) * (N-K-n+i+1)))

pmf_sci = [hypergeom.pmf(i, N, K, n) for i in range(K+1)]
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
# 少しずらして表示する
ax[0].plot(np.arange(K+1)+0.1, pmf, label="Recurrence")
ax[0].plot(np.arange(K+1)-0.1, pmf_sci, label="Scipy")
ax[0].legend()
ax[0].set_title("pmf")

cdf = np.cumsum(pmf)
cdf_sci = [hypergeom.cdf(i, N, K, n) for i in range(K+1)]
ax[1].plot(np.arange(K+1)+0.1, cdf, label="Recurrence")
ax[1].plot(np.arange(K+1)-0.1, cdf_sci, label="Scipy")
ax[1].legend()
ax[1].set_title("cdf")
plt.show()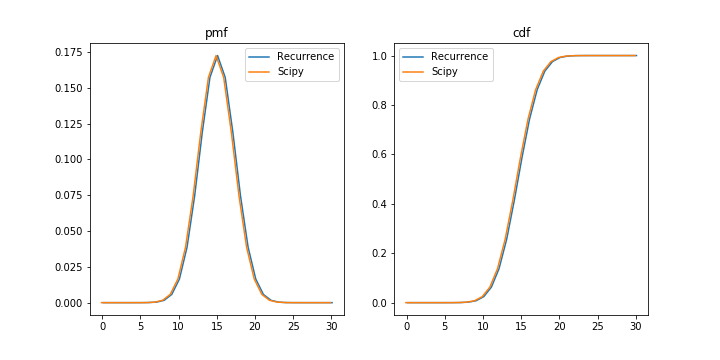

プロットの結果より、scipyとほぼ同じ値をとることがわかった。

なお、確率質量関数のリストpmfを求めておけば、累積分布関数cdfはnp.cumsum(pmf)で計算できる。

注意

今回は特に注意しなかったが、より高い精度が必要となる場合には浮動小数点計算の誤差について十分考慮する必要がある。

具体的には、順列計算の際には有理数ライブラリを使うなどして、可能な限り整数値で計算を行ったほうが良い。