2つの事象のどちらか一方、または両方が起こることを和事象といいます。
この記事では、ベン図を用いて和事象の確率を計算する方法について解説し、それぞれの事象の確率の和との関係について、一般の場合と極限を考えます。
記号の定義
この記事では、和事象と積事象を次の記号であらわします。
- \(A\cup B\) :和事象( \(A\) または \(B\) )
- \(A\cap B\) :積事象( \(A\) かつ \(B\) )
和事象の確率(事象が2つのとき)
定理
事象 \(A, B\) が生じる確率を、それぞれ \(P(A), P(B)\) とおくと、和事象の確率について
$$P(A\cup B)=P(A)+P(B)-P(A\cap B)\tag{1}$$
が成り立ちます。
証明
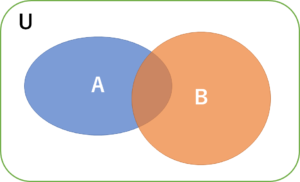
事象 \(A, B\) の関係は上の図のようになります( \(U\) は全事象)。
確率を面積として捉えると、 \(A\cup B\) に相当する面積を求めるためには、 \(A, B\) の面積を足した後、 \(A\cap B\) の面積を引けばよいことがわかります。
和事象の確率(事象が3つのとき)
事象 \(A, B, C\) が生じる確率を、それぞれ \(P(A), P(B), P(C)\) とおくと、
$$P(A\cup B\cup C)=P(A)+P(B)+P(C)$$
$$-P(A\cap B)-P(B\cap C)-P(C\cap A)+P(A\cap B\cap C)\tag{2}$$
が成り立ちます。
図を使った証明
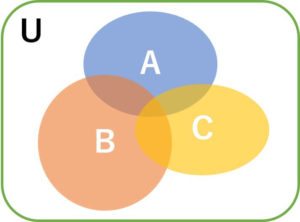
2事象のときと同様に、まず、それぞれの確率 \(P(A), P(B), P(C)\) を足します。
その後、2事象で重複している面積 \(P(A\cap B),P(B\cap C),P(C\cap A)\) を引きます。
すると今度は、3事象で重複した面積 \(P(A\cap B\cap C)\) を引きすぎていることになるので、これを足して終了です。
式を使った証明
$$D=B\cup C$$
とします。
式 \((1)\) より
$$P(A\cup D)=P(A)+P(D)-P(A\cap D)\tag{3}$$
$$P(D)=P(B\cup C)=P(B)+P(C)-P(B\cap C)\tag{4}$$
がそれぞれ成り立ちます。
また
$$P(A\cap D)=P(A\cap (B\cup C))=P(A\cap B)+P(A\cap C)-P(A\cap B\cap C)\tag{5}$$
(それぞれの関係をベン図で確認してください)
より、式 \((4),(5)\) を式 \((3)\) に代入して
$$P(A\cup D)=P(A)+P(B)+P(C)-P(B\cap C)$$
$$-\{P(A\cap B)+P(A\cap C)-P(A\cap B\cap C)\}$$
つまり
$$P(A\cup(B\cup C))=P(A)+P(B)+P(C)$$
$$-P(A\cap B)-P(B\cap C)-P(C\cap A)+P(A\cap B\cap C)$$
となります。
最後に
$$P(A\cup(B\cup C))=P(A\cup B\cup C)$$
より、式 \((2)\) が導かれます。
このように、式 \((1), (5)\) を繰り返し使うことによって、任意の個数について和事象の確率を計算できます。
和事象に関する不等式
事象が2つのとき
式 \((1)\) より
$$P(A\cup B)\leq P(A)+P(B)\tag{6}$$
が成り立ちます。
等号成立は \(A, B\) が排反(同時に起こり得ない)のときです。
なぜならば、 \(A\cap B=\emptyset\) より面積の重なりがなくなるため、 \(P(A\cap B)=0\) であるからです。
事象が3つのとき
不等式 \((6)\) を繰り返し使うことによって
$$P(A\cup B\cup C)=P((A\cup B)\cup C)$$
$$\leq P(A\cup B) + P(C)$$
$$\leq P(A) + P(B) + P(C)$$
が成り立ちます。
一般の場合
\(N\) 個の事象の列 \(\{A_1, A_2, \cdots, A_N\}\) の和事象を
$$\bigcup_{k=1}^{N}A_{k}$$
と書くことにします。
この場合もやはり、不等式 \((6)\) を繰り返し使うことによって
$$P\left(\bigcup_{k=1}^{N}A_{k}\right)\leq\sum_{k=1}^{N}P(A_{k})\tag{7}$$
が導かれます。
これを厳密に定理として表現すると、以下のようになります。
\(\mathfrak{B}\) を可測集合族とする。
事象の列 \(A_{k}\in\mathfrak{B}, k=1,2,\ldots,N\) に対して
$$P\left(\bigcup_{k=1}^{N}A_{k}\right)\leq\sum_{k=1}^{N}P(A_{k})$$
が成り立つ。
$$P\left(\bigcup_{k=1}^{\infty}A_{k}\right)\leq\sum_{k=1}^{\infty}P(A_{k})$$
不等式の極限
不等式 \((7)\) において、 \(N\to\infty\) の極限をとることを考えます。
このとき、以下の定理が成り立ちます。
\(\mathfrak{B}\) を可測集合族とする。
事象の列 \(A_{k}\in\mathfrak{B}, k=1,2,\ldots,\) に対して
$$P\left(\bigcup_{k=1}^{\infty}A_{k}\right)\leq\sum_{k=1}^{\infty}P(A_{k})$$
が成り立つ。
証明
\(B_{n}=\bigcup_{k=1}^{n}A_{k}\) とおくと、 \(B_{n}\) は単調増大列となります。
単調増大列とその性質については、以下の記事でくわしく解説しています。

↑の記事の、確率の連続性に関する定理を用いると
$$P\left(\bigcup_{n=1}^{\infty}B_{n}\right)=\lim_{n\to\infty}P(B_{n})=\lim_{n\to\infty}P\left(\bigcup_{k=1}^{n}A_{k}\right)\leq\lim_{n\to\infty}\sum_{k=1}^{n}P(A_{k})=\sum_{k=1}^{\infty}P(A_{k})$$
が導かれます。
ここで、
$$\bigcup_{n=1}^{\infty}B_{n}=\bigcup_{n=1}^{\infty}\bigcup_{k=1}^{n}A_{k}=\bigcup_{k=1}^{\infty}A_{k}$$
が成り立つことから、これを代入して
$$P\left(\bigcup_{k=1}^{\infty}A_{k}\right)\leq\sum_{k=1}^{\infty}P(A_{k})$$
となります。

Comments