概要
WikipediaのBIC(ベイズ情報量基準)のページを読んでいると、BICは
$$\mathrm{BIC}=-2\cdot\ln(L)+k\ln(n)\tag{1}$$
と定義されるが、ガウス誤差の下では
$$\mathrm{BIC}=n\ln\left(\frac{RSS}{n}\right)+k\ln(n)\tag{2}$$
となる、と書いてあった(変数の意味については上記Wikipediaのページを参照のこと)。
確かにそうなりそうな気はするが、まあ一応ね…ということで導出してみた。
最後にPythonで確認実験も行う。
導出
そもそもガウス誤差モデルとは、「モデルの各予測値と各実測値の誤差が、同一のガウス分布にしたがって生じる」という仮定である。平均 \(\mu\) 、標準偏差 \(\sigma\) の正規分布の確率密度関数は
$$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2\sigma^2}(x-\mu)^2\right)$$
と書けるが、ここでは \(\mu=0\) としても一般性を失わないので
$$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{x^2}{2\sigma^2}\right)\tag{3}$$
とする。対数尤度関数 \(\ln(L)\) は
$$\ln{L}=\ln\left(\prod_{i=1}^{n}p(x_i)\right)$$
$$=\ln\left\{(2\pi\sigma^2)^{-\frac{n}{2}}\exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^{n}{x_i}^2\right)\right\}$$
$$=-\frac{n}{2}\ln(2\pi)-\frac{n}{2}\ln(\sigma^2)-\frac{1}{2\sigma^2}\sum_{i=1}^{n}{x_i}^2\tag{4}$$
と書ける。ここで、分散 \(\sigma^2\) の式
$$\sigma^2=\frac{1}{n}\sum_{i=1}^{n}{x_i}^2$$
を用いて、 \((4)\) 式の第2項に右辺、第3項に左辺の内容をそれぞれ代入すると
$$\ln{L}=-\frac{n}{2}\ln(2\pi)-\frac{n}{2}\ln\left(\frac{\sum_{i=1}^{n}{x_i}^2}{n}\right)-\frac{1}{2\sigma^2}\cdot n\sigma^2$$
$$=-\frac{n}{2}\ln{2\pi}-\frac{n}{2}\ln\left(\frac{\sum_{i=1}^{n}{x_i}^2}{n}\right)-\frac{n}{2}$$
$$=-\frac{n}{2}\ln\left(\frac{\sum_{i=1}^{n}{x_i}^2}{n}\right)-\frac{n}{2}\left(1+\ln(2\pi)\right)$$
となる。最後に、二乗和誤差
$$\mathrm{RSS}=\sum_{i=1}^{n}{x_i}^2$$
を代入して両辺を \(-2\) 倍すると
$$-2\cdot\ln(L)=n\ln\left(\frac{\mathrm{RSS}}{n}\right)+n\left(1+\ln(2\pi)\right)$$
となり、 \((1)\) 式に代入することで
$$\mathrm{BIC}=n\ln\left(\frac{\mathrm{RSS}}{n}\right)+n\left(1+\ln(2\pi)\right)+k\ln(n)$$
が得られるが、第2項は \(n\) にのみ依存し、モデルのパラメータ数 \(k\) が異なる場合でも一定となる。
BIC はパラメータ数が異なるモデル間での大小関係の比較にのみ用いるため、この第2項を脱落(平行移動と考えてもよい)させても問題ない。よって
$$\mathrm{BIC}=n\ln\left(\frac{\mathrm{RSS}}{n}\right)+k\ln(n)$$
とBICを再定義して \((2)\) 式を得る。
実験
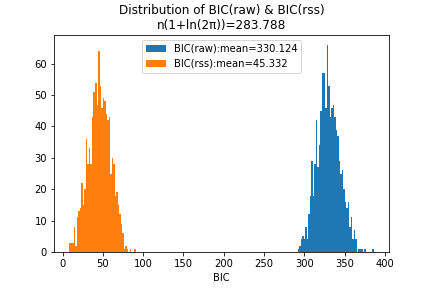
各 BIC の分布
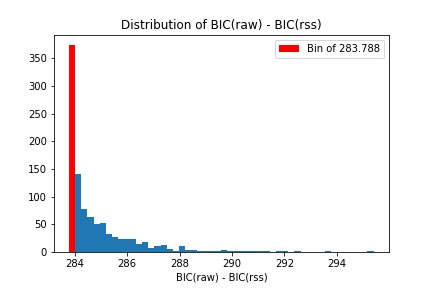
BIC の差の分布
コード
本来の定義通り計算した場合と、 RSS に基づいて計算した場合とでは \(n(1+\ln(2\pi))\) 程度の差があるが、ヒストグラムの形状比較から、これはおおよそ平行移動にすぎないことがわかる。

Comments