EMアルゴリズムを混合正規分布に適用した際の計算方法については、例えば以下の記事で紹介されている。

しかし、一般の場合(正規分布以外の混合分布)についてのEMアルゴリズムの実践例は、あまり紹介されていない。
この記事では、混合正規分布の場合に限らない任意の確率分布に対するEMアルゴリズムについて、理論を簡単に説明した後、実践例をコードとともに提示する。
理論
表記法
EMアルゴリズムでは、データ \(\mathbf{X}=(x_1,x_2,\ldots,x_N)\) を用いて、混合分布
$$p(x|\mathbf{\Theta})=\sum_{k=1}^{K}\pi_k p_k(x|\theta_k)\tag{1}$$
の各パラメータについて最尤推定を行う。
ここで \(\pi_k\) は混合率と呼ばれ、混合分布の各分布 \(p_k(x|\theta_k)\) がどんな割合で混ぜられているかを表現している。
また、各分布の混合率とパラメータ \(\theta_k\) をまとめて混合分布全体のパラメータ \(\mathbf{\Theta}\) と表記する。
潜在変数の導入
性質
混合分布から実際にデータが生成される状況を考えると、混合率にしたがって1つの分布が選ばれ、その分布関数にしたがってデータ点が得られると理解できる。
このとき、潜在変数 \(\mathbf{Z}=\{z_{nk}\}\) によって、各データ点 \(x_n\) がどの分布から来たかを表現することを考える。
ここでは、
$$z_{nk}=\begin{cases}1&x_n\text{は}k\text{番目の分布から生成された}\\0&\text{それ以外}\end{cases}$$
と書くことにする。
この潜在変数は実際に観測することはできないが、\(\mathbf{X},\mathbf{\Theta}\) に基づいてその期待値を計算することができる。
また、この潜在変数を考えることによって、各分布はそれが関与するデータ点に関してのみ(とくに、強く関与する点を重視して)、最適化を行えばよいことがわかる。
公式
潜在変数を用いると、データと潜在変数の同時分布の尤度関数は次のように書ける。
$$p(\mathbf{X}, \mathbf{Z}|\mathbf{\Theta})=\prod_{n=1}^N\prod_{k=1}^K\left\{\pi_k p_k(x_n|\theta_k)\right\}^{z_{nk}}\tag{2}$$
この関数はまた後に登場する。
以下に証明を載せるが、読み飛ばしてもらって構わないし、はじめは感覚的な理解で問題ない。
証明
\(z_{nk}=1\) となる確率は混合率によって決まり、
$$p(z_{nk}=1|\pi_k)=\pi_k$$
である。
\(x_n\) に関する潜在変数をまとめたベクトル \(\mathbf{z_n}=(z_{n1},z_{n2},\ldots,z_{nK})\) を定義すると、この要素のうち1つだけが \(1\) 、その他が \(0\) の値をとる(1-of-K符号化法)。
相乗記号を用いることで、このベクトルの分布は
$$p(\mathbf{z_n}|\pi_1,\ldots,\pi_K)=\prod_{k=1}^K\pi_k^{z_{nk}}$$
と書ける。
同様にして、すべての \(n\) について潜在変数の分布をまとめると
$$p(\mathbf{Z}|\pi_1,\ldots,\pi_K)=\prod_{n=1}^N\prod_{k=1}^K\pi_k^{z_{nk}}\tag{3}$$
となる。
また潜在変数の定義より、\(z_{nk}=1\) のとき、 \(x_n\) は \(k\) 番目の分布から生じる。
すなわち
$$p(x_n|z_{nk}=1,\theta_k)=p_k(x_n|\theta_k)$$
と書ける。
潜在変数をベクトルにまとめると
$$p(x_n|\mathbf{z}_n,\theta_1,\ldots,\theta_K)=\prod_{k=1}^K p_k(x_n|\theta_k)^{z_{nk}}$$
すべての \(n\) について考え、 \(\mathbf{X}\) に対する尤度関数としてまとめると
$$p(\mathbf{X}|\mathbf{Z},\theta_1,\ldots,\theta_K)=\prod_{n=1}^N\prod_{k=1}^K p_k(x_n|\theta_k)^{z_{nk}}\tag{4}$$
最後に、確率の連鎖律より
$$p(\mathbf{X}|\mathbf{Z},\theta_1,\ldots,\theta_K)p(\mathbf{Z}|\pi_1,\ldots,\pi_K)=p(\mathbf{X},\mathbf{Z}|\pi_1,\ldots,\pi_K,\theta_1,\ldots,\theta_K)=p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})$$
となる。
途中、 \(\pi_1,\ldots,\pi_K,\theta_1,\ldots,\theta_K\) をパラメータ \(\mathbf{\Theta}\) にまとめた。
式 \((3),(4)\) を代入して
$$p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})=\prod_{n=1}^N\prod_{k=1}^K p_k(x_n|\theta_k)^{z_{nk}}\prod_{n=1}^N\prod_{k=1}^K\pi_k^{z_{nk}}=\prod_{n=1}^N\prod_{k=1}^K \{\pi_k p_k(x_n|\theta_k)\}^{z_{nk}}$$
問題点と解決法
混合分布の最尤推定では
- 各データ点はどこから来たか(潜在変数)
- 各分布はどんな形をしているか(パラメータ)
の2点を同時に最適化しなければならないので難しい。
EMアルゴリズムでは、「1.を固定した状態で2.を最適化」⇆「2.を固定した状態で1.を最適化」というプロセスを繰り返すことによって、全体の最適化を行う。
アルゴリズムの導出
EMアルゴリズムの目標
データ \(\mathbf{X}\) に対する混合分布の尤度関数 \(p(\mathbf{X}|\mathbf{\Theta})\) を考える。
EMアルゴリズムの目標は、この \(p(\mathbf{X}|\mathbf{\Theta})\) または対数尤度関数 \(\ln p(\mathbf{X}|\mathbf{\Theta})\) を最大化するパラメータ \(\mathbf{\Theta}\) を求めることである。
下界の設定
尤度関数に潜在変数を導入して、同時分布の尤度関数 \(p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})\) について考えると、確率の連鎖律により
$$p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})=p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})p(\mathbf{X}|\mathbf{\Theta})$$
が成り立つ。
これを変形して以下の式 \((3)\) を得る。
このとき、 \(q(\mathbf{Z})\) は潜在変数の分布であるが、以下の式変形はこれをどのようにとるかに関わらず、常に実行可能である。
$$\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})=\ln p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})+\ln p(\mathbf{X}|\mathbf{\Theta})$$
$$\ln p(\mathbf{X}|\mathbf{\Theta})=\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})-\ln p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})$$
$$\ln p(\mathbf{X}|\mathbf{\Theta})=\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})-\ln p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})-\ln q(\mathbf{Z})+\ln q(\mathbf{Z})$$
$$\ln p(\mathbf{X}|\mathbf{\Theta})=\ln\frac{p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})}{q(\mathbf{Z})}-\ln\frac{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})}{q(\mathbf{Z})}$$
$$q(\mathbf{Z})\ln p(\mathbf{X}|\mathbf{\Theta})=q(\mathbf{Z})\ln\frac{p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})}{q(\mathbf{Z})}-q(\mathbf{Z})\ln\frac{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})}{q(\mathbf{Z})}\tag{5}$$
$$\ln p(\mathbf{X}|\mathbf{\Theta})=\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})}{q(\mathbf{Z})}-\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})}{q(\mathbf{Z})}\tag{6}$$
なお、式 \((5)\rightarrow(6)\) の変形では、 \(q(\mathbf{Z})\) は確率分布なので、 \(\mathbf{Z}\) についての総和をとると \(1\) になることを用いた。
ここで、式 \((6)\) の第2項はカルバック-ライブラーダイバージェンス(KLダイバージェンス)
$$\mathrm{KL}(q||p)=-\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})}{q(\mathbf{Z})}$$
であり、第1項も
$$\mathcal{L}(q,\mathbf{\Theta})=\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})}{q(\mathbf{Z})}$$
と定義することで
$$\ln p(\mathbf{X}|\mathbf{\Theta})=\mathcal{L}(q,\mathbf{\Theta})+\mathrm{KL}(q||p)\tag{7}$$
と書ける。
なお、 \(\mathcal{L}(q,\mathbf{\Theta})\) という表記は、これが \(\mathbf{\Theta}\) によって制御されると同時に、関数 \(q(\mathbf{Z})\) の形状にも依存する汎関数であることを示している。
KLダイバージェンスが常に非負となることを考慮すると、対数尤度関数と \(\mathcal{L}(q,\mathbf{\Theta})\) の間には
$$\ln p(\mathbf{X}|\mathbf{\Theta})\geq\mathcal{L}(q,\mathbf{\Theta})$$
という関係が成り立つ。
すなわち、 \(\mathcal{L}(q,\mathbf{\Theta})\) は対数尤度関数の下界を定めていることがわかる。
下界の最大化1( \(q\) を更新)
等式 \((7)\) において、対数尤度関数 \(\ln p(\mathbf{X}|\mathbf{\Theta})\) は関数 \(q(\mathbf{Z})\) の形状に依存せず一定である一方、右辺の2項の値は共に \(q\) に依存するため、下界とKLダイバージェンスはトレードオフの関係にあることがわかる。
KLダイバージェンス \(\mathrm{KL}(q||p)\) は
$$q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})$$
となるときに最小値 \(0\) をとる。
すなわち、潜在変数の分布 \(q(\mathbf{Z})\) を事後分布 \(p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})\) として定めることで、下界は最大値をとり、対数尤度関数と等しくなる。
なお、 \(\mathbf{Z}\) の事後分布 \(p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})\) の具体的な形状を求めることは困難だが、 \(\mathbf{Z}\) の各要素 \(z_{nk}\) の期待値については、各データ点 \(x_n\) に対する各分布 \(p_k\) の尤度×混合率 \(\pi_k\) の比
$$\mathbb{E}[z_{nk}]=\frac{\pi_{k} p_{k}(x_{n}|\theta_{k})}{\sum_{j=1}^{K}\pi_j p_j(x_n|\theta_j)}\tag{8}$$
として求められる。
この期待値のことを負担率と呼ぶ。
下界の最大化2( \(\mathbf{\Theta}\) の更新)
次に、 \(q\) ではなく \(\mathbf{\Theta}\) を更新して下界を更に増加させることを考える。
ここで、更新前後を区別するため、これまで考えてきた更新前のパラメータを \(\mathbf{\Theta}\rightarrow\mathbf{\Theta}^\text{old}\) と書き直し、更新後のパラメータを \(\mathbf{\Theta}^\text{new}\) と書くことにする。
また、いわゆる「更新途中の」パラメータ、すなわち、下界を最大化しているわけではない任意のパラメータは \(\mathbf{\Theta}\) と表記するので、混同しないように注意してほしい。
「下界の最大化1」の結果、KLダイバージェンス最小化のために
$$q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta^\text{old}})$$
と定めたことから、下界の方程式は以下のように書き換えられる。
$$\mathcal{L}(q,\mathbf{\Theta})=\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta^\text{old}})\ln\frac{p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})}{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta^\text{old}})}$$
$$\mathcal{L}(q,\mathbf{\Theta})=\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})+\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})\ln p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})$$
この式の右辺において、第2項は \(\mathbf{\Theta}\) によらず一定である。
よって下界の最大化のためには第1項のみを考えれば良く、これを
$$\mathcal{Q}(\mathbf{\Theta},\mathbf{\Theta}^{\text{old}})=\sum_{\mathbf{Z}}p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})$$
とおく。
この量の意味するところは、「潜在変数の事後分布に関して、同時分布の対数尤度関数の期待値をとる」ということである。
すなわち
$$\mathcal{Q}(\mathbf{\Theta},\mathbf{\Theta}^{\text{old}})=\mathbb{E}_{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})}[\ln p(\mathbf{X},\mathbf{Z}|\mathbf{\Theta})]$$
$$=\mathbb{E}_{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^\text{old})}\left[\sum_{n=1}^{N}\sum_{k=1}^{K}z_{nk}\left\{\ln\pi_k+\ln p_k(x_n|\theta_k)\right\}\right]$$
$$=\sum_{n=1}^{N}\sum_{k=1}^{K}\mathbb{E}[z_{nk}]\left\{\ln\pi_k+\ln p_k(x_n|\theta_k)\right\}\tag{9}$$
となり、ここに式 \((8)\) の期待値を代入することで、最適化すべき具体的な関数形が求まる。
アルゴリズムの収束性
\(\mathcal{Q}(\mathbf{\Theta},\mathbf{\Theta}^{\text{old}})\) を最大化する \(\mathbf{\Theta}\) の値を \(\mathbf{\Theta}^{\text{new}}\) とすると、下界について
$$\mathcal{L}(q,\mathbf{\Theta}^{\text{new}})\geq\mathcal{L}(q,\mathbf{\Theta}^{\text{old}})$$
が成り立つ。
さらに、対数尤度関数と下界の関係から
$$\ln p(\mathbf{X}|\mathbf{\Theta}^{\text{new}})\geq\mathcal{L}(q,\mathbf{\Theta}^{\text{new}})\geq\mathcal{L}(q,\mathbf{\Theta}^{\text{old}})=\ln p(\mathbf{X}|\mathbf{\Theta}^{\text{old}})$$
より、一連の操作によって尤度が高められていることがわかる。
また、尤度が高くなった場合には
$$\ln p(\mathbf{X}|\mathbf{\Theta}^{\text{new}})=\mathcal{L}(q,\mathbf{\Theta}^{\text{new}})+\mathrm{KL}(q||p)$$
$$\ln p(\mathbf{X}|\mathbf{\Theta}^{\text{new}})=\mathcal{L}(q,\mathbf{\Theta}^{\text{new}})-\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta}^{\text{new}})}{q(\mathbf{Z})}$$
においてKLダイバージェンスは \(0\) ではなく、再び \(q\) の更新を行うことによって最尤推定を前進させることができる。
まとめ
EMアルゴリズム
上記の \(q, \mathbf{\Theta}\) の更新操作を、EMアルゴリズムではそれぞれEステップ/Mステップと呼称し、これらを繰り返すことでパラメータ推定を行う。
Eステップ (Expectation step)
\(q(\mathbf{Z})\) の更新に対応する。
パラメータを \(\mathbf{\Theta}^{\text{old}}\) に固定して
$$\mathbb{E}[z_{nk}]=\frac{\pi_{k} p_{k}(x_{n}|\theta_{k})}{\sum_{j=1}^{K}\pi_j p_j(x_n|\theta_j)}$$
で表される潜在変数の期待値を計算する。
Mステップ (Maximization step)
\(\mathbf{\Theta}\) の更新に対応する。
潜在変数の分布 \(q(\mathbf{Z})\) を \(p(\mathbf{Z}|\mathbf{X},\mathbf{\Theta})\) に固定し、その期待値 \(\mathbb{E}[z_{nk}]\) を用いて
$$\mathcal{Q}(\mathbf{\Theta},\mathbf{\Theta}^{\text{old}})=\sum_{n=1}^{N}\sum_{k=1}^{K}\mathbb{E}[z_{nk}]\left\{\ln\pi_k+\ln p_k(x_n|\theta_k)\right\}\tag{10}$$
を最大化するパラメータの組 \(\mathbf{\Theta}^{\text{new}}\) を求める。
実践
データ \(\mathbf{X}\)
一様分布 \(U(x|0, 0.5)\) から発生させたデータ点200個と、指数分布 \(\mathrm{Ex}(x|\frac{1}{2})=\frac{1}{2}\exp\left(-\frac{x}{2}\right)\) から発生させたデータ点800個を結合した、計 \(N=1000\) 個をデータ \(\mathbf{X}\) とする。
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(42)
# exponentialのscaleはλの逆数であることに注意
x = np.hstack((np.random.random(size=200) * 0.5, np.random.exponential(size=800, scale=2)))
plt.hist(x, bins=200)
plt.ylabel("number")
plt.xlabel("value")
plt.title("Histogram of X")
plt.tight_layout()
plt.savefig("hist_x.png")
plt.show()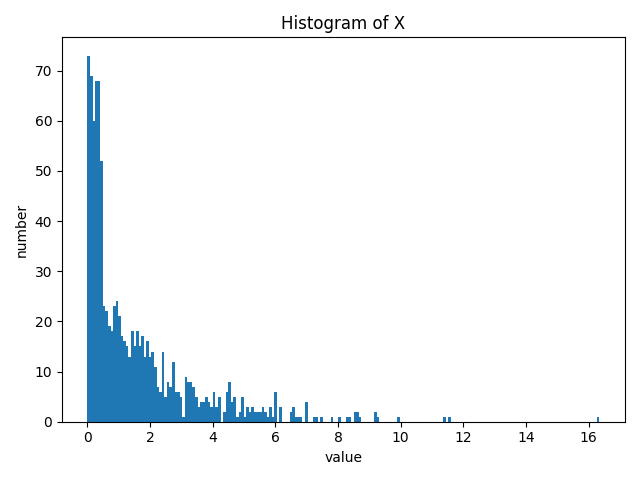
混合分布
上記のデータを用いて、2種類の分布からなる以下の混合分布について最尤推定する。
$$p(x|\rho, \sigma, \lambda)=\rho\sqrt{\frac{2}{\pi \sigma^2}}\exp\left(-\frac{x^2}{2\sigma^2}\right)+(1-\rho)\lambda\exp(-\lambda x)\tag{11}$$
円周率 \(\pi\) との混同を避けるため、混合率の記号には \(\rho\) を用い、また混合率の和が \(1\) となることから、2種類の分布の混合率をそれぞれ \(\rho, 1-\rho\) と表した。
2種類の分布はともに \([0,\infty)\) の範囲で定義され、第2項はパラメータ \(\lambda\) の指数分布である。
第1項は平均 \(\mu=0\) 、標準偏差 \(\sigma\)の正規分布の負の部分を、 \(x=0\) を境に正の方向へ折り曲げて重ねたものに等しい。
なぜここで、一様分布+指数分布という組み合わせではなく、上記のような混合分布を用いるのかについては、記事末尾に記載する。
def p1(x, sigma):
return np.sqrt(2/(np.pi*sigma*sigma)) * np.exp(-x*x/(2*sigma*sigma))
def p2(x, lamb):
return lamb * np.exp(-lamb * x)
def likelihood(x, rho, sigma, lamb):
return rho * p1(x, sigma) + (1 - rho) * p2(x, lamb)Eステップ
パラメータを \(\rho^{\text{old}}, \sigma^{\text{old}}, \lambda^{\text{old}}\) に固定して、潜在変数の期待値
$$\mathbb{E}[z_{n1}]=\frac{\rho^{\text{old}}\sqrt{\frac{2}{\pi (\sigma^{\text{old}})^2}}\exp\left(-\frac{x^2}{2(\sigma^{\text{old}})^2}\right)}{\rho^{\text{old}}\sqrt{\frac{2}{\pi(\sigma^{\text{old}})^2}}\exp\left(-\frac{x^2}{2(\sigma^{\text{old}})^2}\right)+(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}$$
$$\mathbb{E}[z_{n2}]=\frac{(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}{\rho^{\text{old}}\sqrt{\frac{2}{\pi(\sigma^{\text{old}})^2}}\exp\left(-\frac{x^2}{2(\sigma^{\text{old}})^2}\right)+(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}=1-\mathbb{E}[z_{n1}]$$
を計算する。
def e_step(x, rho, sigma, lamb):
e1 = rho * p1(x, sigma) / likelihood(x, rho, sigma, lamb)
return e1, 1 - e1Mステップ
式 \((2)\) より、データと潜在変数の同時分布の尤度関数は
$$p(\mathbf{X}, \mathbf{Z}|\rho, \sigma, \lambda)=\prod_{n=1}^{N}\left\{\rho\sqrt{\frac{2}{\pi \sigma^2}}\exp\left(-\frac{x_n^2}{2\sigma^2}\right)\right\}^{z_{n1}}\left\{(1-\rho)\lambda\exp(-\lambda x_n)\right\}^{z_{n2}}$$
であり、対数をとって
$$\ln p(\mathbf{X}, \mathbf{Z}|\rho, \sigma, \lambda)=\sum_{n=1}^{N}\left[z_{n1}\left\{\ln\rho+\frac{1}{2}(\ln 2-\ln\pi-2\ln\sigma)-\frac{x_n^2}{2\sigma^2}\right\}+z_{n2}\left\{\ln(1-\rho)+\ln\lambda-\lambda x_n\right\}\right]$$
となる。
式 \((10)\) より、この同時分布の対数尤度関数の期待値について、Eステップで求めた結果をもとに計算することで、
$$\mathcal{Q}(\rho, \sigma, \lambda, \rho^{\text{old}}, \sigma^{\text{old}}, \lambda^{\text{old}})=\sum_{n=1}^{N}\left[\mathbb{E}[z_{n1}]\left\{\ln\rho+\frac{1}{2}(\ln 2-\ln\pi-2\ln\sigma)-\frac{x_n^2}{2\sigma^2}\right\}+\mathbb{E}[z_{n2}]\left\{\ln(1-\rho)+\ln\lambda-\lambda x_n\right\}\right]$$
を最適化したらよいことがわかる。
\(\rho\) について微分し、その値を \(0\) とすると
$$\frac{\partial Q}{\partial \rho}=\sum_{n=1}^{N}\left(\frac{\mathbb{E}[z_{n1}]}{\rho}-\frac{\mathbb{E}[z_{n2}]}{1-\rho}\right)$$
$$=\frac{1}{\rho(1-\rho)}\sum_{n=1}^{N}\{(1-\rho)\mathbb{E}[z_{n1}]-\rho\mathbb{E}[z_{n2}]\}$$
$$=\frac{1}{\rho(1-\rho)}\sum_{n=1}^{N}\{(1-\rho)\mathbb{E}[z_{n1}]-\rho(1-\mathbb{E}[z_{n1}])\}$$
$$=\frac{1}{\rho(1-\rho)}\sum_{n=1}^{N}(\mathbb{E}[z_{n1}]-\rho)=0$$
より
$$\frac{1}{\rho(1-\rho)}\sum_{n=1}^{N}\mathbb{E}[z_{n1}]=\frac{N\rho}{\rho(1-\rho)}$$
$$\frac{1}{\rho(1-\rho)}\sum_{n=1}^{N}\mathbb{E}[z_{n1}]=\frac{N}{1-\rho}$$
$$\rho=\frac{1}{N}\sum_{n=1}^{N}\mathbb{E}[z_{n1}]\tag{12}$$
となり、これが \(\rho^{\text{new}}\) である。
\(\sigma, \lambda\) についても同様に、
$$\frac{\partial Q}{\partial \sigma}=\sum_{n=1}^{N}\mathbb{E}[z_{n1}]\left(-\frac{1}{\sigma}+\frac{x_n^2}{\sigma^3}\right)=0$$
$$\sum_{n=1}^{N}\mathbb{E}[z_{n1}]\frac{x_n^2}{\sigma^3}=\sum_{n=1}^{N}\frac{\mathbb{E}[z_{n1}]}{\sigma}$$
$$\sum_{n=1}^{N}\mathbb{E}[z_{n1}]x_n^2=\sigma^2\sum_{n=1}^{N}\mathbb{E}[z_{n1}]$$
$$\sigma=\sqrt{\frac{\sum_{n=1}^{N}\mathbb{E}[z_{n1}]x_n^2}{\sum_{n=1}^{N}\mathbb{E}[z_{n1}]}}.\tag{13}$$
$$\frac{\partial Q}{\partial \lambda}=\sum_{n=1}^{N}\mathbb{E}[z_{n2}]\left(\frac{1}{\lambda}-x_n\right)=0$$
$$\frac{1}{\lambda}\sum_{n=1}^{N}\mathbb{E}[z_{n2}]=\sum_{n=1}^{N}\mathbb{E}[z_{n2}]x_n$$
$$\lambda=\frac{\sum_{n=1}^{N}\mathbb{E}[z_{n2}]}{\sum_{n=1}^{N}\mathbb{E}[z_{n2}]x_n}.\tag{14}$$
と更新後の値が求まる。
def m_step(x, e1, e2):
r_tmp = e1.mean()
s_tmp = np.sqrt((e1*x*x).sum()/e1.sum())
l_tmp = e2.sum()/(e2*x).sum()
return r_tmp, s_tmp, l_tmp結果
パラメータの初期値を \(\rho=0.5,\sigma=1.0,\lambda=1.0\) として、Eステップ/Mステップによる更新を100回行った。
rho = 0.5
sigma = 1.0
lamb = 1.0
like = [] # 対数尤度を記録
for i in range(101):
if i % 10 == 0:
print("iter={:>3} | rho={:.3f}, sigma={:.3f}, lamb={:.3f}".format(i, rho, sigma, lamb))
e1, e2 = e_step(x, rho, sigma, lamb)
rho, sigma, lamb = m_step(x, e1, e2)
like.append(np.log(likelihood(x, rho, sigma, lamb)).sum())
データ点のうち、一様分布から生じたものの割合が \(\frac{200}{1000}=0.250\ldots\) であることから \(\rho\) の値は妥当であり、 \(\lambda\) の値もほぼ正確に算出されている。
また、イテレーションが進むごとに尤度も大きくなっていることがわかる。
plt.plot(like)
plt.ylabel("log-likelihood")
plt.xlabel("iter")
plt.tight_layout()
plt.savefig("log_likelihood.png")
plt.show()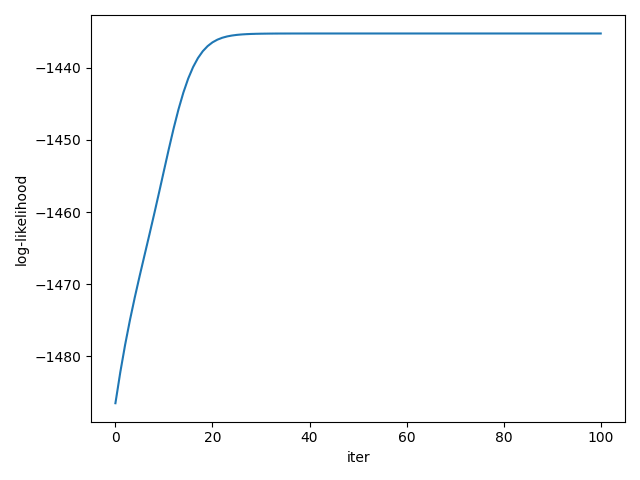
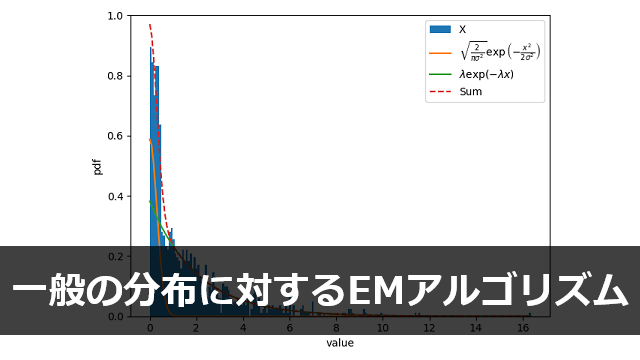
確率分布関数をヒストグラムと重ねて表示すると次のようになる。
_, b, _ = plt.hist(x, bins=200, density=True, label="X")
uni = p1(b, alpha)*rho
exp = p2(b, lamb)*(1-rho)
plt.plot(b, uni, label=r"$\frac{1}{\alpha}$")
plt.plot(b, exp, label=r"$\lambda\exp(-\lambda x)$")
plt.plot(b, uni + exp, linestyle="--", label="Sum")
plt.legend()
plt.ylabel("pdf")
plt.xlabel("value")
plt.ylim(0, 1)
plt.tight_layout()
plt.savefig("hist_and_dist_uni.png")
plt.show()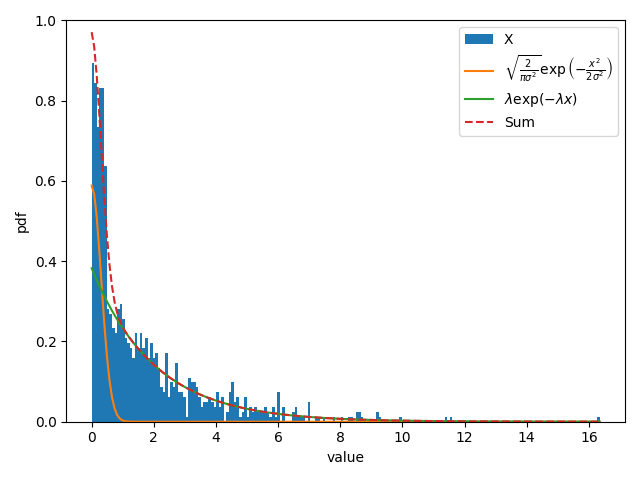
(参考)
データ \(\mathbf{X}\) は本来、一様分布が \([0, 0.5]\) の区間に生成した矩形を、指数分布に由来する数値の集合に合わせた形状をしている。
それを反映するように、緑色で表された指数分布が不要な部分を無視して、自身に由来するデータのみにフィットできていることが見て取れる。
補足
「一様分布と指数分布から生成されたデータを、なぜ一様分布と指数分布の組み合わせではない混合分布で最尤推定するのか」という疑問はもっともだと思う。
しかし、EMアルゴリズムを適用するに際し、一様分布のような明確な境界を持つ分布を使用すると、少し特殊な配慮が必要になる。
このことに関しては、以下の記事で検討する。


Comments