概要
この記事では、臨床試験等で優越性・非劣性・同等性の検証を行う際に、必要なサンプル数を計算する手法について解説する。サンプルサイズは、検出したい平均差と標準偏差を設定し、試験実施者が望む検出力の強度を与えることによって算出できる。最後に、割付比や予想脱落率に基づいて、サンプルサイズの微修正を行う手法についても紹介する。
本文
サンプルサイズの意義
実際に試験を行う前に、解析のために集めるサンプルサイズを決定しておくことには重要な意義がある。
第一に、サンプルサイズが不足していると、仮に有意な差があったとしてもそれを検出できない。そして逆に、サンプルサイズが多すぎると、有意でない差を検出してしまうことがある。
事前にデータの分布や期待する検出力を設定し、過不足ない数のサンプルのみを解析することで、こうした誤検出を避けることができる。
(追記:2021/02/11)サンプルサイズサイズが大きすぎる場合の問題点について補足しました。

サンプルサイズの決定法
優越性試験
「薬Aは薬Bに比べて、有意に血圧を低下させるか?」のような効果を検証する試験を優越性試験という。この試験では薬Aと薬Bの効果の差(平均差)を検定し、このときの帰無仮説 \(H_0\) と対立仮説 \(H_1\) は
- \(H_0\) :「薬Aと薬Bの血圧低下効果に差がない」
- \(H_1\) :「薬Aと薬Bの血圧低下効果に差がある」
と書ける。
ここで、結果が \(H_0, H_1\) のそれぞれとなるときのデータの分布を考える。
その際、事前に以下の値について想定しておく。
- \(\delta\) :薬Aと薬Bの間に効果の差があった場合、それはどのくらいの大きさか(検出したい平均差)
- (=どのくらいの差を検出したいか)
- \(\sigma\) :データの標準偏差
例えば標準偏差の場合、データの (最大値 - 最小値) / 5 でその値を近似計算できる。
今、サンプルサイズをとりあえず \(N\) と書くと、 \(H_0, H_1\) に対応するそれぞれの分布を正規分布と仮定して、
- \(H_0\) : \(\mathcal{N}(0, \frac{2\sigma^2}{N})\)
- \(H_1\) : \(\mathcal{N}(\delta, \frac{2\sigma^2}{N})\)
とおくことができる。以下、これを図示する。
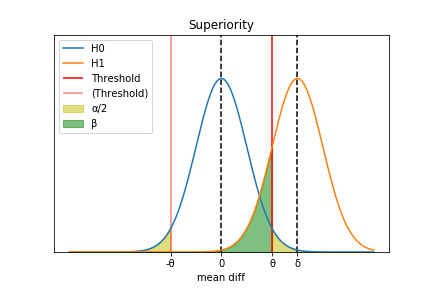

図では \(\delta\) とは別に、検定の閾値(Threshold)として \(\theta\) を設定した。
値が \(\theta\)( \(-\theta\) )を上回った(下回った)ときに薬Aは薬Bよりも効果が強い(弱い)と判定する。
この結果、第1種過誤 \(\frac{\alpha}{2}\)(\(H_0\) が正しい時に \(H_1\) と判定する)と第2種過誤 \(\beta\)( \(H_1\) が正しい時に \(H_0\) と判定する)の2種類の間違いが生まれる。
なお、第1種過誤のみ2で割られているのは、この検定が両側検定であるためである。
図中の値を用いて方程式を作ることを考える。
標準正規分布 \(\mathcal{N}(x|0, 1)\) の面積について
$$a=\int_{-infty}^{Z_a}\mathcal{N}(x|0, 1)dx$$
と表現し、 \(O(0, 0), T(\theta, 0), D(\delta, 0)\) と点を設定すると、
$$OT=Z_{1-\frac{\alpha}{2}}\times\frac{\sqrt{2}\sigma}{\sqrt{N}}$$
$$TD=Z_{1-\beta}\times\frac{\sqrt{2}\sigma}{\sqrt{N}}$$
$$\delta=OT+TD$$
より
$$\delta=(Z_{1-\frac{\alpha}{2}}+Z_{1-\beta})\sqrt{\frac{2}{N}}\sigma$$
$$N=2[Z_{1-\frac{\alpha}{2}}+Z_{1-\beta}]^2\left(\frac{\sigma}{\delta}\right)^2$$
と \(N\) について解くことができる。
ここで、「検出したい平均差」と「標準偏差」の比 \(\frac{\delta}{\sigma}\) を Effect size(ES)と定義し、過誤の割合を \(\alpha=0.05, \beta=0.20\) と設定すると、 \(Z_{1-\frac{0.05}{2}}=Z_{0.975}\simeq1.96, Z_{1-0.2}=Z_{0.8}\simeq0.84\) より
$$N\simeq16\div {ES}^2$$
となる。
\(\alpha\) の値は基本的に両側 \(0.05\) と設定されることが多い。
\(1-\beta\) は検出力(Power)と呼ばれ、通常 \(80\%\) 以上に設定される。
以上の結果をまとめると、優越性試験のサンプルサイズは以下のように計算される。
$$N\simeq16\div {ES}^2\qquad(Power=80\%)$$
$$N\simeq21\div {ES}^2\qquad(Power=90\%)$$
非劣性試験
「新薬Aは既存薬Bに比べて、血圧低下効果が劣らないといえるか?」のような効果を検証する試験を非劣性試験という。
この試験では、薬A,Bの効果の差についての許容できる限度として、非劣性マージン \(\delta\) を設定し、その値を超過するか否かを検証する。
帰無仮説 \(H_0\) と対立仮説 \(H_1\) は以下のとおりである。
- \(H_0\) :「薬Aと薬Bの効果の差は、 \(\delta\) 以上である」
- \(H_1\) :「薬Aと薬Bの効果の差は、 \(\delta\) 未満である」
したがって、判別閾値 \(\theta\) を別途設定して図示すると、以下のようになる。
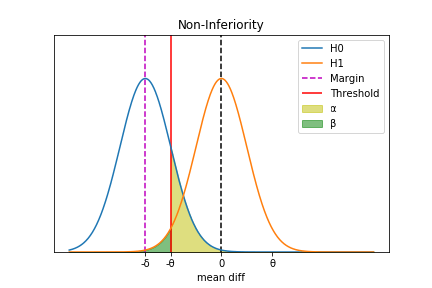

優越性試験と同様に計算すると、
$$N=2[Z_{1-\alpha}+Z_{1-\beta}]^2\div {ES}^2$$
が得られる。
ここで \(\alpha\) の値が2で割られていないのは、非劣性試験が片側検定であるためである。
同等性試験
「新薬Aは既存薬Bに比べて、血圧低下効果が同等であるといえるか?」のような効果を検証する試験を同等性試験という。
この試験では、薬A,Bの効果の差について同等とみなせる範囲として、同等域 \([-\epsilon, \epsilon]\) を設定し、その中に収まるか否かを検証する。
帰無仮説 \(H_0\) と対立仮説 \(H_1\) は以下のとおりである。
- \(H_0\) :「薬Aと薬Bの効果の差は、 \(-\epsilon\) 以下または \(\epsilon\) 以上である」
- \(H_1\) :「薬Aと薬Bの効果の差は、 \(-\epsilon\) 超かつ \(\epsilon\) 未満である」
これまでと同様に、判別閾値(範囲) \([-\theta, \theta]\) を別途設定して図示すると、以下のようになる。
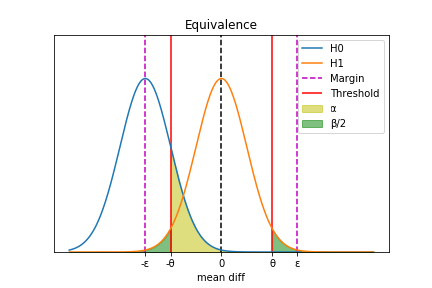

図では \(H_0\) の分布を \(H_1\) より平均が小さくなる形で表示したが、逆方向に存在することもありうる。
しかしいずれにせよ、第1種誤差が生じるのは一方( \([-\theta, \theta]\) の範囲内)のみであり、対して第2種誤差は両側に生じることに変わりはない。
したがって、これまでと同様に計算して
$$N=2[Z_{1-\alpha}+Z_{1-\frac{\beta}{2}}]^2\div {ES}^2$$
が得られる。
サンプルサイズの修正
割付比による修正
前述のような薬Aと薬Bの試験の場合、被検者は通常 \(1:1\) に割り振られる。
しかし、時として \(A:B=1:k\) のように被検者を割り付けたい時があり、この場合はサンプルサイズの修正を必要とする。
手順は以下の通り。
- 「サンプルサイズの決定法」で述べた方法によって、 \(1:1\) 割付けを行うときのサンプル数 \(N\) を計算する。
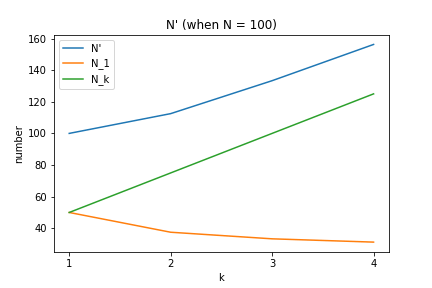
- \(1:k\) 割付けでのサイズ \(N'\) は
$$N'=\frac{(1+k)^2}{4k}N$$
となる。 - 少ない群に \(\frac{N'}{1+k}\) を割り当てる。
- 多い群に \(N'-\frac{N'}{1+k}\) を割り当てる。

脱落率による修正
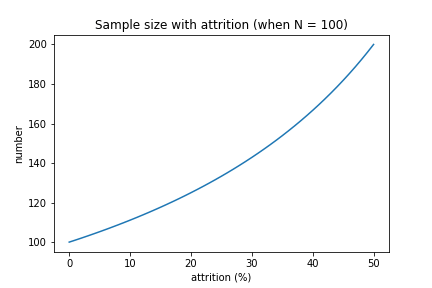
試験中に被検者の脱落が予想される場合は、その予測値に合わせて、あらかじめ多くサンプルサイズを設定しておく。
具体的には、「サンプルサイズの決定法」で述べた方法によって得られたサンプルサイズを \(N\) とし、脱落率を \(x\%\) とすると
$$\frac{100}{100-x}N$$
のサンプル数が必要となる。


Comments