エントロピーの最大化による正規分布の導出

正規分布は「エントロピーを最大化する」という性質を持った確率分布であるため、統計学で重宝されています。

この記事では、正規分布、エントロピー、確率密度関数の意味について確認し、これらを用いて正規分布を導出します。

また、導出に際して汎関数や変分法についても解説します。

前提
正規分布の導出
正規分布の特徴

前提

正規分布

１次元の正規分布は、確率密度関数が以下の式で定義される確率分布です。

$$\mathcal{N}(x|\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{1}{2\sigma^2}(x-\mu)^2\right\}$$

正規分布は平均 $\mu$ 、分散 $\sigma^2$ の２種類のパラメータを持ちます。

確率密度関数

確率密度関数は連続型の確率変数の確率分布をあらわす関数です。

確率質量関数とは異なり、積分を用いて確率を表現します。

このあたりの用語の関係性は、以下の記事を参照してください。

【図解】確率変数と確率密度関数を正確に、そして直観的に理解する

確率論で用いられる確率質量関数と確率密度関数について、確率変数の定義から出発して、実例や用途に基づいて直観的に解説します。これらの用語は非常に誤解しやすいのですが、この記事を読むことで、それぞれの正確な意味を押さえ、関連する性質や定理についての理解を早めることができるようになります。

エントロピー

エントロピーは「状況の不確実さの程度」をあらわす指標です。

連続型の確率変数 $x$ に対する確率密度関数 $p(x)$ から、エントロピーは

$$H[p]\equiv\int_{-\infty}^{\infty}p(x)\{-\ln p(x)\}dx \tag{1}$$

と計算できます。

情報理論にもとづくエントロピーの定義と、確率変数が離散的な場合のエントロピーの最大化については、以下の記事を参照してくだざい。

情報量/エントロピーの定義と意味を、具体例から導出する

情報理論では、情報量やエントロピー（平均情報量）を用いて、出来事（事象）に対する「驚き」や、未来に対する「不確実さ」を表現します。この記事では、具体例から情報量とエントロピーの自然な定義を導出し、それらが何に使えるのか？どのような性質を持つのか？について解説します。

汎関数と変分法

$(1)$ 式で表されるエントロピーは、関数 $p(x)$ の形状によってその値を変えるため、「関数の関数」と考えることができます。

このように、関数を引数として受け取ってスカラーとしての値を返す関数のことを汎関数といい、それを最大化する関数 $p(x)$ を求めるためには変分法の原理を使用します。

汎関数の定義・性質と、変分法の一般例に関しては、以下の記事を参照してください。

汎関数と変分法について、わかりやすく解説

「関数の関数」と呼ばれる汎関数と、汎関数を最大化（最小化）する変分法について解説します。汎関数は通常の「関数-引数」の関係を、「汎関数-関数」の関係にそのまま置き換えることで簡単に理解できます。同様に変分法も、極値を極値関数に置き換えたものと大差ありません。

正規分布の導出

導出の方針

変分法を用いて、汎関数 $H[p]$ としてあらわしたエントロピーを最大化する確率密度関数 $p(x)$ を求めます。

その際、以下の制限がかかることに注意します。

規格化条件（確率は全領域で積分すると１になる）

$p(x)$ は確率密度関数（＝積分により確率を表現する関数）であるため、規格化条件

$$\int_{-\infty}^{\infty}p(x)dx=1 \tag{2}$$

をみたします。

つまり、 $p(x)$ を $(-\infty, \infty)$ の範囲で積分すると１になります。

平均と分散の定義式

また、 $p(x)$ が平均 $\mu$ 、分散 $\sigma^2$ を持つとすると、それぞれの定義より

$$\int_{-\infty}^{\infty}p(x)(x-\mu)dx=0 \tag{3}$$
$$\int_{-\infty}^{\infty}p(x)(x-\mu)^2=\sigma^2 \tag{4}$$

が成り立ちます。

ラグランジュの未定乗数法

$(2),(3),(4)$ 式を、（それぞれの式）=0となるように変形します。

それぞれの左辺にラグランジュ乗数 $\lambda_1, \lambda_2, \lambda_3$ を掛けて対象関数 $H[p]$ から引き、その式を最適化すると、対象関数を $(2),(3),(4)$ の制約条件のもとで最適化することができます。

これをラグランジュの未定乗数法といいます。

つまり

$$\Phi[p]=H[p]-\lambda_1\int_{-\infty}^{\infty}p(x)dx-\lambda_2\int_{-\infty}^{\infty}p(x)(x-\mu)dx-\lambda_3\int_{-\infty}^{\infty}p(x)(x-\mu)^2dx$$

$$\Phi[p]=\int_{-\infty}^{\infty}[p(x)\{-\ln p(x)\}-\lambda_1p(x)-\lambda_2p(x)(x-\mu)-\lambda_3p(x)(x-\mu)^2]dx$$

とおいて、 $\Phi[p]$ を最適化します。

変分法の適用

この汎関数 $\Phi[p]$ を最大化するため、一次変分 $\delta\Phi[p]$ がゼロとなる関数 $p(x)$ を求めます。

ここで、 $\Phi[p]$ は $p(x)$ の導関数に依存しない関数なので

$$F(x,p)=p(x)\{-\ln p(x)\}-\lambda_1p(x)-\lambda_2p(x)(x-\mu)-\lambda_3p(x)(x-\mu)^2$$

とおくと

$$\delta\Phi[p]=\int_{-\infty}^{\infty}F_p(x,p)\delta p\,dx$$

$$=\int_{-\infty}^{\infty}\{-\ln p-1-\lambda_1-\lambda_2(x-\mu)-\lambda_3(x-\mu)^2\}\delta p\,dx=0$$

となります。

すなわち、任意の $x$ について

$$\ln p+1+\lambda_1+\lambda_2(x-\mu)+\lambda_3(x-\mu)^2=0 \tag{5}$$

が成り立ちます。

この関係式より、 $\ln p$ が $x-\mu$ の２次関数になっていることがわかります。

ここで、 $p$ が規格化条件を満たすためには $x \to \pm \infty$ において $p \to 0$ となる必要があります。

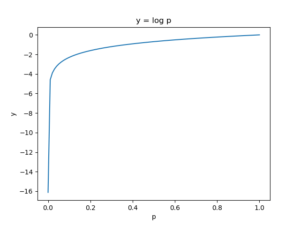
任意の $x$ において $0 < p < 1$ となることより、この範囲で $y = \log p$ のグラフについて考えると

import numpy as np
from matplotlib import pyplot as plt

p = np.linspace(1e-7,1,100)
y = np.log(p)
plt.plot(p,y)
plt.title("y = log p")
plt.xlabel("p")
plt.ylabel("y")
plt.show()

$p \to 0$ のとき、 $\log p \to -\infty$ となるので、 $(5)$ 式の２次関数は上に凸となります。

したがって $p$ は

$$p(x) = C\exp\{-\alpha^2(x-\beta)^2\}$$

$$= C\exp(-\alpha^2x^2+2\alpha^2\beta x-\alpha^2\beta^2)$$

の形に限られます。

ここで、ガウス積分（ $a > 0$ のとき）

$$\int_{-\infty}^{\infty}\exp(-ax^2+bx+c)dx = \sqrt{\frac{\pi}{a}}\exp(\frac{b^2}{4a}+c) \tag{6}$$
$$\int_{-\infty}^{\infty}x^2\exp(-ax^2)dx = \frac{1}{2a}\sqrt{\frac{\pi}{a}} \tag{7}$$

を用いると、 $(2)$ 式の規格化条件と $(6)$ 式より

$$\int_{-\infty}^{\infty}C\exp(-\alpha^2x^2+2\alpha^2\beta x-\alpha^2\beta^2)dx$$

$$=C\sqrt{\frac{\pi}{\alpha^2}}\exp(\frac{4\alpha^4\beta^2}{4\alpha^2}-\alpha^2\beta^2)$$

$$=C\sqrt{\frac{\pi}{\alpha^2}}=1$$

より

$$C=\frac{\alpha}{\sqrt{\pi}}$$

を示すことができます。

また、 $(3)$ 式の平均値の条件より

$$\int_{-\infty}^{\infty}C\exp\{-\alpha^2(x-\beta)^2\}(x-\mu)dx = 0$$

となりますが、 $\beta=\mu$ のとき、この条件はみたされます。

なぜならば、 $\beta=\mu,\,y=x-\mu$ とおき、左辺の変数を置換すると

$$(左辺) = C\int_{-\infty}^{\infty}e^{y^2}y\,\frac{dy}{dx}\,dx = C\int_{-\infty}^{\infty}e^{y^2}y\,dx$$

となりますが、ここで $f(y)=e^{y^2}y$ とおくと

$$f(-y) = e^{(-y)^2}(-y) = -e^{y^2}y = -f(y)$$

より、被積分関数は奇関数となり、奇関数を区間 $(-\infty,\infty)$ で積分すると０になるためです。

最後に、 $(4)$ 式の分散の条件と $(7)$ 式より（再び $y=x-\mu$ とおく）

$$\int_{-\infty}^{\infty}\frac{\alpha}{\sqrt{\pi}}\exp\{-\alpha^2(x-\beta)^2\}(x-\mu)^2dx = \int_{-\infty}^{\infty}\frac{\alpha}{\sqrt{\pi}}\exp\{-\alpha^2(x-\mu)^2\}(x-\mu)^2dx$$

$$=\int_{-\infty}^{\infty}\frac{\alpha}{\sqrt{\pi}}\exp(-\alpha^2y^2)y^2\,\frac{dy}{dx}\,dx$$

$$=\frac{\alpha}{\sqrt{\pi}}\int_{-\infty}^{\infty}y^2\exp(-\alpha^2y^2)dy$$

$$=\frac{\alpha}{\sqrt{\pi}}\cdot\frac{1}{2\alpha^2}\sqrt{\frac{\pi}{\alpha^2}}= \sigma^2$$

すなわち

$$\alpha^2 = \frac{1}{2\sigma^2}$$

となります。

以上より

$$p(x) = \frac{\sqrt{\frac{1}{2\sigma^2}}}{\sqrt{\pi}}\exp\{-\frac{1}{2\sigma^2}(x-\mu)\}$$

$$=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\{-\frac{1}{2\sigma^2}(x-\mu)\}$$

として、正規分布が導かれました。

正規分布の特徴

正規分布が平均値と分散の制約のもとでエントロピーを最大にする理由は、以下のように考えられます。

エントロピーは不確定度を表す指標であり、それを最大化するためには、全体にまんべんなく広がった分布であることが望ましいです。

しかし、それでは分散の条件を満たさなくなるため、分布はある程度の範囲に収まっていなければなりません。

その意味で正規分布は、分散の制約を満たしながら可能な限り広がった分布であるといえます。