確率論で用いられる確率質量関数と確率密度関数について、確率変数の定義から出発して、実例や用途に基づいて直観的に解説します。
これらの用語は非常に誤解しやすいのですが、この記事を読むことで、それぞれの正確な意味を押さえ、関連する性質や定理についての理解を早めることができるようになります。
確率変数
定義
確率変数とは、確率論において、起こり得る事柄(事象)に割り当てられている数(通常、整数や実数など)を値として取る変数のことです。
確率変数の例
以下、実例を挙げながら、確率変数には離散確率変数と連続確率変数の2種類があることを説明します。
ここでは確率変数を \(x\) で表します。
離散確率変数

「サイコロの出目」について考えると、 \(x\) は \(x=1,2,3,4,5,6\) の6種類の値(事象)を取り得ます。
このように、事象の数が有限な確率変数を離散確率変数といいます。
連続確率変数

「時計の長針の位置」について考えると、 \(x\) は \(0\leq x< 60\) 分の範囲の実数値をとります。
(このとき、12.345...分なども考えています。桁数を無限に増やせるので、事象の数も無限です)
このように、事象の数が無限になる確率変数を連続確率変数といいます。
確率を表す関数
前章で定義した離散確率変数と連続確率変数のそれぞれに関して、各事象が生じる確率を表現する関数を考えます。
確率質量関数
サイコロ(離散確率変数)の場合、事象 \(x\) が生じる確率を \(P(x)\) と書くことにすると、
$$P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=\frac{1}{6}$$
と書けます。
このような関数を確率質量関数という。
確率の総和が1(100%)になるという前提から、全事象を重量1の物体とみなします。
そして、各事象に確率を重みとして割り当てていくことから「質量」という名前が付きました。
確率密度関数
連続確率変数に関する問題
時計の長針の位置(連続確率変数)の場合も同様に、事象 \(x\) が生じる確率を \(P(x)\) と書くことにします。
このとき、 \(P(30)\) の値はいくつになるでしょうか?
これを確率質量関数と見た場合、「長針が30分を指している確率」となります。
長針が任意の位置にある確率はすべて等しいのですが、起こりうる事象は無限にあるため、サイコロと同様に考えると
$$P(30)=\frac{1}{\infty}=0$$
となってしまいます。
これはすべての実数について成り立つことから、連続確率変数に対しては、個々の事象に確率(質量)を割り当てることができないことがわかります。
確率「密度」の考え方
そこで連続確率変数の場合は、事象ではなく範囲に確率を割り当てます。
たとえば、「長針が30分から45分の間にある確率」について考えた場合、この値は \(\frac{1}{4}\) とすぐに求められます。
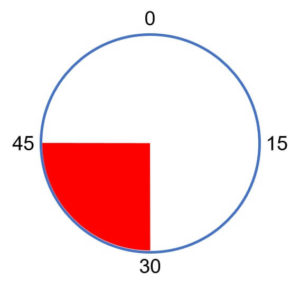
この確率 \(P[30\leq x< 45]\) を、積分を用いて以下のように表現することを考えます。
$$P[30\leq x< 45]=\int^{45}_{30}p(x)dx=\frac{1}{4}$$
ここで、積分の中に現れた関数 \(p(x)\) を確率密度関数といいます。
今回は各事象ではなく、事象の範囲に確率質量を割り当てています。
そのため、質量を範囲の単位で割った確率密度が各事象に与えられていることから、この名前がつきました。
確率密度関数の値の意味
長針の場合、各事象が生じる確率は等価であることから、確率密度関数 \(p(x)\) の値が事象 \(x\) によらず
$$p(x)=a$$
と定数値をとることを仮定します。
確率は全事象の区間で積分すると1になることから
$$P[0\leq x< 60]=\int^{60}_{0}p(x)dx=\int^{60}_{0}adx$$
$$=[ax]^{60}_{0}=60a=1$$
より
$$p(x)=a=\frac{1}{60}$$
が導けます。
つまり事象 \(x\) によらず
$$p(0)=p(30)=p(60)=p(12.345\cdots)=\frac{1}{60}$$
となりますが、これらはたとえば「長針が30分の位置にある確率が \(\frac{1}{60}\) である」ことを意味するのではありません。
なぜならば、これは確率密度を表したものであり、その値は積分の結果でのみ意味を持つからです。
実際、確率密度関数を「30分」という点で積分しても、その値はゼロになります。
定義
以上の議論を踏まえて、確率密度関数を正確に定義します。
確率変数 \(x\) が、 \(a\leq x\leq b\) の範囲の値をとる確率を \(P[a\leq x\leq b]\)とすると、
$$P[a\leq x\leq b]=\int_{a}^{b}p(x)dx$$
が成り立つとき、 \(p(x)\) を確率密度関数という。
確率密度関数の条件
定義より、確率変数 \(x\) が、 \(x\) から \(x+dx\) までの領域の値を取るときの確率は、長方形の計算から \(p(x)dx\) となります。
また、確率変数 \(x\) の定義域を \({\bf R}\) とすると、全体確率は1となることより、
$$\int_{\mathbf{R}}p(x)dx=1$$
をみたします。
上式の条件を、規格化条件といいます。
また、確率密度関数は常に非負値になります。
したがって、 \(p(x)\) が確率密度関数であるための本質的な条件は以下の2点です。
$$\int_{\mathbf{R}}p(x)dx=1 \tag{1}$$
$$p(x)\geq 0 \tag{2}$$
多変数への応用
これまでは確率変数が1次元の場合を考えてきましたが、 \(M\) 次元確率変数 \(\mathbf{x}\) についても
$$P[\mathbf{a}\leq\mathbf{x}\leq \mathbf{b}]=\int_{\mathbf{a}}^{\mathbf{b}}p(\mathbf{x})d\mathbf{x}$$
を満たす確率密度関数 \(p(\mathbf{x})\) を定義でき、確率変数 \(\mathbf{x}\) が、 \(\mathbf{x}\) から \(\mathbf{x}+d\mathbf{x}\) までの領域の値を取る確率は \(p(\mathbf{x})d\mathbf{x}\) となります。
このとき
$$d\mathbf{x}=\prod_{i=1}^{M}dx_i$$
です。
\(M=2\) における状況を図示して説明すると、
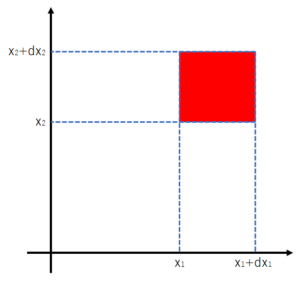
\(d\mathbf{x}=dx_1dx_2\) は上図の面積に等しくなります。
これに \(p(\mathbf{x})\) を掛けると確率になることから、 \(p(\mathbf{x})\) は単位面積当たりの確率と考えることができます。
この関係からも、確率「密度」の意味が明確になっています。
また \(M\geq 3\) の場合も、 \(d\mathbf{x}=dx_1dx_2\cdots dx_M\) を体積に相当するものと考えることで同様の議論が成り立ちます。
確率密度関数の周辺化
\(M\) 次元確率変数 \(\mathbf{x}=(x_1,x_2,\cdots,x_M)\) に対する確率密度関数 \(p(\mathbf{x})\) について、 \(x_3\) から \(x_M\) までのみ積分を行った結果を \(f(x_1,x_2)\) とします。
このとき
$$f(x_1,x_2)=\int_{\mathbf{R}}p(\mathbf {x})dx_3 dx_4 \cdots dx_M$$
となります。
ここで、 \(p(\mathbf{x})\geq 0\) であることから、 \(f(x_1,x_2)\geq 0\) です。
また、 \(f(x_1,x_2)\) を \(x_1\) と \(x_2\) について積分すると
$$\int_{\mathbf{R}}f(x_1,x_2)dx_1dx_2=\int_{\mathbf{R}}(\int_{\mathbf{R}}p(\mathbf{x})dx_3 dx_4 \cdots dx_M)dx_1dx_2$$
$$=\int_{\mathbf{R}}p(\mathbf{x})dx_1dx_2dx_3 dx_4 \cdots dx_M$$
$$=\int_{\mathbf{R}}p(\mathbf{x})d\mathbf{x}=1$$
より、 \((1),(2)\) 式をみたします。
よって、 \(f(x_1,x_2)\) は \(2\) 次元の確率変数 \((x_1,x_2)\) についての確率密度関数となります。
このように、 \(M\) 次元確率変数に対する確率密度関数を不要な \(N\,(N< M)\) 次元についてのみ積分することで、必要な \(M-N\) 次元確率変数に対する確率密度関数を求めることができます。
この手法を周辺化といい、得られた確率密度関数(今回の場合は \(f\) )のことを周辺分布といいます。
また、もともとの分布のことは、周辺分布に対して同時分布または結合分布と呼びます。


Comments