ROC曲線とPR曲線は、検査や機械学習の分類に対する性能を判定する方法です。
この手法を用いることで、検査の感度や陽性的中率のトレードオフを考慮しながら、性能を判定・比較することができます。
この記事では、具体例を用いてROC曲線・PR曲線の書き方を説明し、それぞれを状況別に使い分ける方法について解説します。
「すべての閾値」で検査性能を評価する
評価指標にはトレードオフがある
通常、検査は何かを測定したり計算したりした値に対し、閾値を基準に陽性/陰性を分類することで設計されます。
検査の性能を評価するための指標は色々ありますが、閾値を操作することで、指標がとる値を調整できます。
ただし、これらの指標の多くは互いにトレードオフの関係にあるため、ある指標では性能が良くても、別の指標ではボロボロということが起こり得ます。
具体例
タンパク質 \(A\) の値から、病気を判定する検査を考えます。
病気の人3名と、健康な人7名のタンパク質 \(A\) を測定し、測定値の順番に並び替えると、次のようになりました。
| 順位 | 状態 | \(A\) の値 |
|---|---|---|
| 1 | 病気 | 100 |
| 2 | 健康 | 98 |
| 3 | 病気 | 97 |
| 4 | 健康 | 92 |
| 5 | 病気 | 88 |
| 6 | 健康 | 70 |
| 7 | 健康 | 69 |
| 8 | 健康 | 69 |
| 9 | 健康 | 50 |
| 10 | 健康 | 42 |
以下、閾値を変化させながら混同行列を書き、
- 感度(真陽性率; TPR)(再現率; Recall)
- 偽陽性率(FPR)
- 陽性的中率(適合率; Presision)
を評価していきます。
混同行列は下図の形で、検査結果をまとめた行列です。
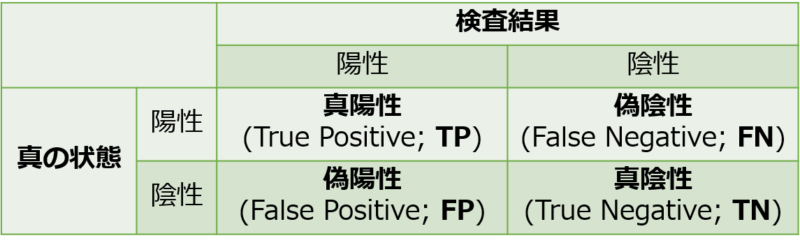
混同行列と、そこから計算される指標については以下の記事を参照してください。
閾値が99のとき
| 検査陽性 | 検査陰性 | |
|---|---|---|
| 病気である | 1 | 2 |
| 病気でない | 0 | 7 |
$$(感度)=\frac{1}{1+2}\fallingdotseq 0.333$$
$$(偽陽性率)=\frac{0}{0+7}=0.000$$
$$(陽性的中率)=\frac{1}{1+0}=1.000$$
閾値を厳しく設定することによって、偽陽性率と陽性的中率がともに完璧な状態になっています。
ただし、感度は低くなっていることに注目してください。
閾値が96のとき
| 検査陽性 | 検査陰性 | |
|---|---|---|
| 病気である | 2 | 1 |
| 病気でない | 1 | 6 |
$$(感度)=\frac{2}{2+1}\fallingdotseq 0.667$$
$$(偽陽性率)=\frac{1}{1+6}\fallingdotseq 0.143$$
$$(陽性的中率)=\frac{2}{2+1}\fallingdotseq 0.667$$
感度が上昇しましたが、その代償として偽陽性率と陽性的中率が悪化しました。
閾値が87のとき
| 検査陽性 | 検査陰性 | |
|---|---|---|
| 病気である | 3 | 0 |
| 病気でない | 2 | 5 |
$$(感度)=\frac{3}{3+0}=1.000$$
$$(偽陽性率)=\frac{2}{2+5}\fallingdotseq 0.286$$
$$(陽性的中率)=\frac{3}{3+2}\fallingdotseq 0.600$$
感度が100%になり、偽陽性率と陽性的中率がさらに悪化しました。
感度が上限に達したので、閾値をこれより小さくしても、偽陽性率と陽性的中率がただ下がっていくだけです。
ただし、最終的に偽陽性率は100%になるのに対し、陽性的中率は常に病気3名分の正解を含むためゼロにはなりません。
閾値と指標の関係まとめ
タンパク質 \(A\) の測定値の横に、その値までを「陽性」と判定した場合の指標を並べて表示します。
| 順位 | 状態 | \(A\) の値 | 感度 | 偽陽性率 | 陽性的中率 |
|---|---|---|---|---|---|
| (ダミー) | \(\infty\) | 0.000 | 0.000 | - | |
| 1 | 病気 | 100 | 0.333 | 0.000 | 1.000 |
| 2 | 健康 | 98 | 0.333 | 0.143 | 0.500 |
| 3 | 病気 | 97 | 0.667 | 0.143 | 0.667 |
| 4 | 健康 | 92 | 0.667 | 0.286 | 0.500 |
| 5 | 病気 | 88 | 1.000 | 0.286 | 0.600 |
| 6 | 健康 | 70 | 1.000 | 0.429 | 0.500 |
| 7 | 健康 | 69 | 1.000 | 0.571 | 0.429 |
| 8 | 健康 | 69 | 1.000 | 0.714 | 0.375 |
| 9 | 健康 | 50 | 1.000 | 0.857 | 0.333 |
| 10 | 健康 | 42 | 1.000 | 1.000 | 0.300 |
これを見ると、感度と偽陽性率が0と1の間を直線的に変化するのに対し、陽性的中率は増減を経て低下傾向にあることがわかります。
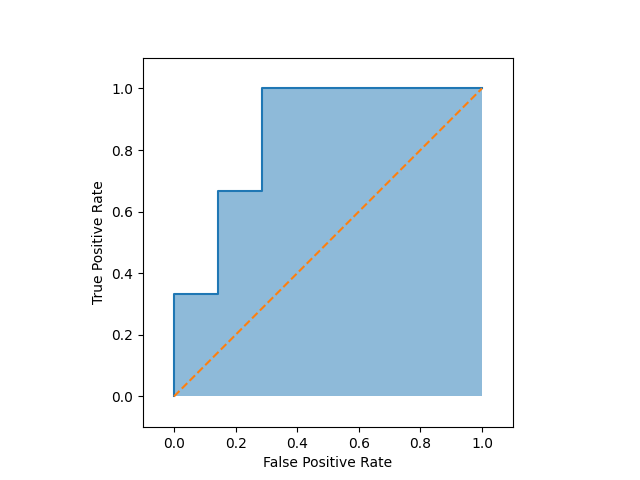
ROC曲線
ROC曲線(Receiver Operating Characteristic Curve)は、感度(真陽性率; TPR)と偽陽性率(FPR)のトレードオフをプロットした図です。
プロットの作成方法
縦軸にTPR、横軸にFPRをプロットします。
タンパク質 \(A\) の検査の場合、下図のようになります。
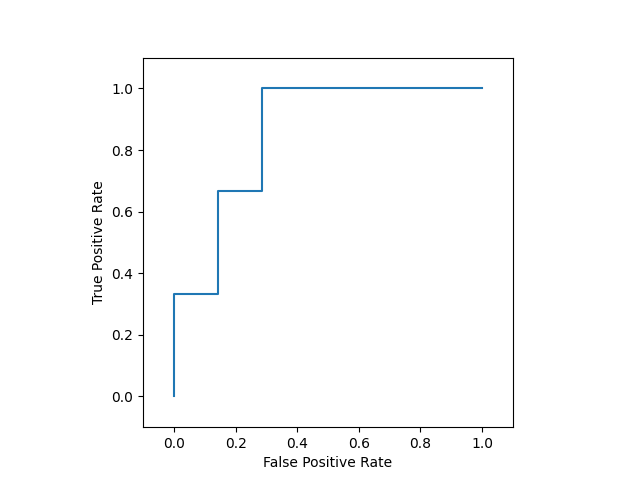
感度と偽陽性率の特徴を反映して、曲線は点 \((0, 0), (1, 1)\) を通り、右肩上がりになります。
AUCによる性能評価と基準
ROC曲線の下にできる面積(Area Under the Curve; AUC)の大きさによって、検査の性能を評価することができます。
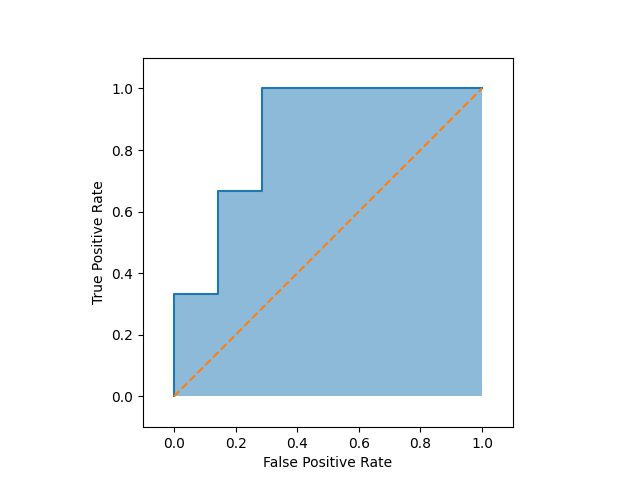
$$AUC=0.857$$
ROC曲線をプロットするのが、タテヨコ0から1の範囲をとる面積1の正方形なので、AUCも0から1の範囲をとります。
また、「病気」と「健康」がランダムに並ぶ(つまり、検査に効果がない)場合、十分にデータの量が多いと、ROC曲線は点 \((0, 0), (1, 1)\) を結ぶ対角線になるため、その場合のAUC=0.5が「検査に意味がない」の基準になります。
そして一般に、AUCが0.8を超えると良い検査とみなされるようです。
逆にAUCが0.5を下回る場合は、逆効果の検査であると考えられますが、閾値と陽性・陰性の関係を反転することで、有用な検査を作ることができます。
(予言が90%外れる占い師の逆をやっていれば得をするのと同じ話)
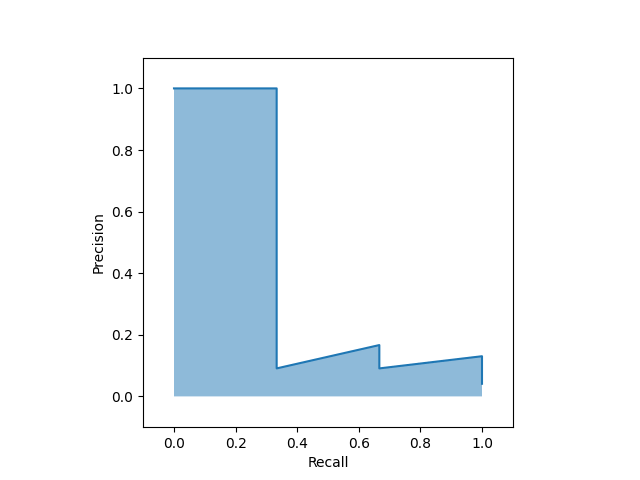
PR曲線
PR曲線(Precision-Recall Curve)は、感度(再現率; Recall)と陽性的中率(Precision)のトレードオフをプロットした図です。
プロットの作成方法
縦軸にPrecision、横軸にRecallをプロットします。
タンパク質 \(A\) の検査の場合、下図のようになります。
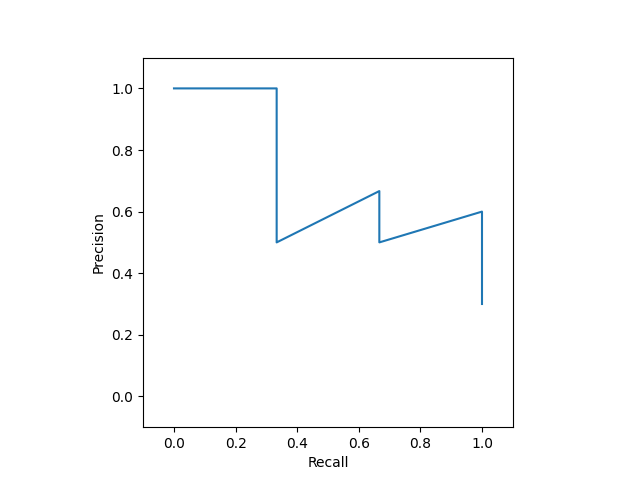
陽性的中率が直線的な変化をしないため、曲線は全体として右肩下がり傾向ですが、増減をくりかえします。
また、点 \((0, 0), (1, 1)\) を通るとは限らないので、プロットする際には軸の描画範囲に注意が必要です。
AUCによる性能評価と基準
ROC曲線と同様に、PR曲線のAUCの大きさによって、検査の性能を評価することができます。
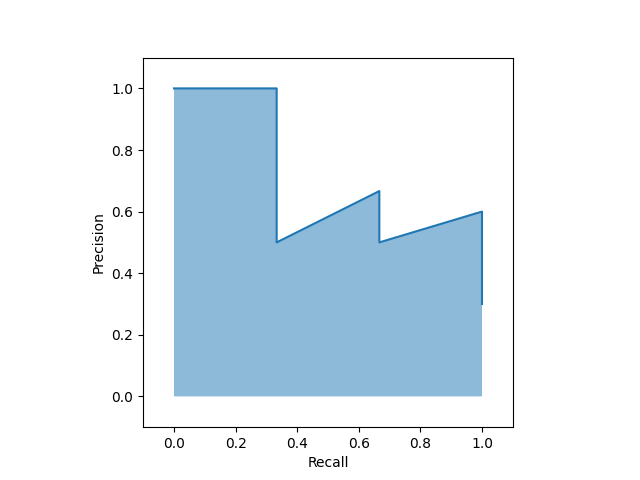
$$AUC=0.711$$
値も同じく0から1の範囲をとります。
ただし、ROC曲線のように「良い検査」を決める一般的な基準が存在しない点が異なります。
さらに、「意味のない検査」の曲線が対角線上に乗るわけでもないため、AUCが0.5を下回っても「悪い検査」であるとは限りません。
(むしろ、「良い検査」のPR-AUCが0.3前後ということは普通にある)
ROC曲線・PR曲線の使い分け
Davis J, Goadrich M. (2006)では
ROC曲線のAUCを最適化するアルゴリズムは、PR曲線のAUCの最適化を保証しない
(筆者訳)
ことが示されています。
そのため、ROC曲線とPR曲線の性質をふまえ、状況に応じた使い分けをする必要があります。
結論から言うと
- 偏りの大きいデータに対しては、PR曲線を使う
- 明確な基準がほしいときは、ROC曲線を使う
という使い分けが推奨されています。
偏りの大きいデータにはPR曲線を使う
病気である/病気でない、の人数に偏りがあり、どちらか一方のみが多いデータを歪みのあるデータといいます。
一般に、病気である人の人数は、健康な人に比べてかなり少なくなるため、データに歪みがある方が普通ともいえます。
このようなデータに対しては、ROC曲線ではなくPR曲線にもとづいて検査を評価した方が良いとされています。
PR曲線は上位の結果のみをハイライトする
ROC曲線に比べ、PR曲線は、測定値が上位のデータ内での分類結果をハイライトする傾向にあります。
ネガティブケースが豊富な場合は、ネガティブデータが並ぶことがわかりきっている下位のデータよりも
ポジティブとネガティブが混在するであろう上位の分類結果に着目した方が、検査の性能評価がしやすいため、歪んだデータに対してはPR曲線による評価が優れているとされています。
結果が明白なところは無視して、怪しくなるところでの分類性能に注目したい、というわけです。
実際、タンパク質 \(A\) の検査の例で、閾値が \(\infty-90\) の範囲をとるときの結果が曲線のどこに相当するかを考えると、
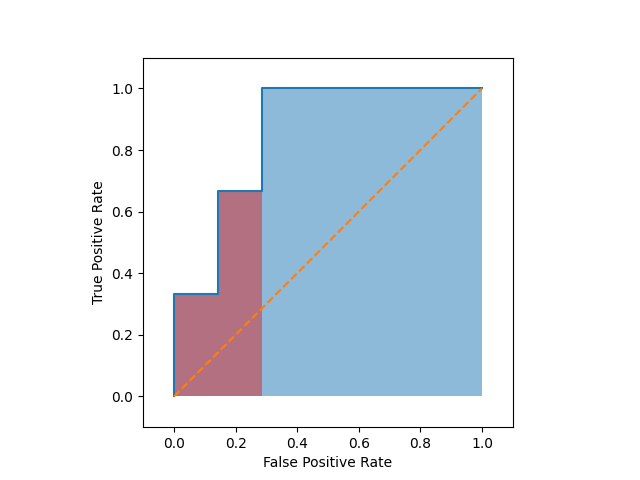
ROC曲線は横軸の \(0-0.286\) であるのに対し
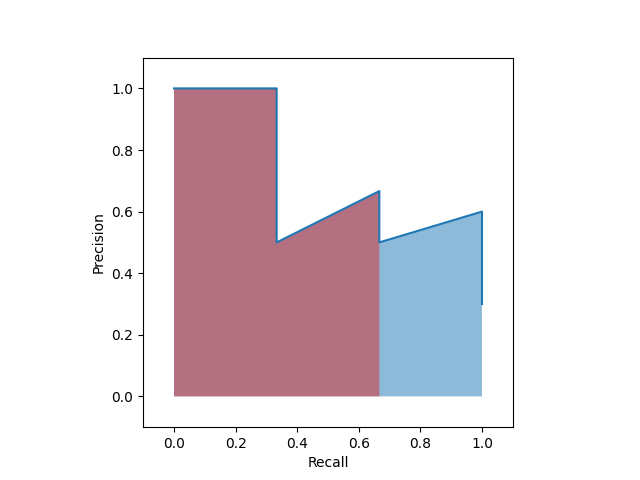
PR曲線では横軸の \(0-0.667\) をカバーしていることがわかります。
つまり、PR曲線の場合、上位の少数のデータに対する結果だけで曲線のほとんどを説明していることになります。
(実験)健康な人の割合を増やしてみる
有病率が低下した場合のROC曲線とPR曲線の変化を観察するため、タンパク質 \(A\) の検査の例で、健康な人の測定値をそのままに、人数を10倍にしてみます。
つまり、測定値のランキングが以下のようになるよう修正します。
| 順位 | 状態 | \(A\) の値 |
|---|---|---|
| 1 | 病気 | 100 |
| 2~11 | 健康 | 98 |
| 12 | 病気 | 97 |
| 13~22 | 健康 | 92 |
| 23 | 病気 | 88 |
| 24~33 | 健康 | 70 |
| 34~43 | 健康 | 69 |
| 44~53 | 健康 | 69 |
| 54~63 | 健康 | 50 |
| 64~73 | 健康 | 42 |
このとき、たとえば閾値が95の状況では、2名の病気の人を検出するために、10名もの健康な人に陽性判定を下してしまっています。
これを反映して、PR曲線では、もともと0.711だったAUCが大きく低下します。
$$AUC=0.413$$
一方、ROC曲線の結果は変化しません。
$$AUC=0.857$$
AUCの結果もまったく同じです。
したがって、検査の陽性/陰性と病気である/病気でないの正解・不正解について、ROC曲線は有病率からみた比率が同じであれば変化しないのに対し、
PR曲線は絶対数を反映し、鋭敏に変化することがわかります。
明確な基準がほしいときはROC曲線
一方、PR曲線のAUCには「良い」とされる明確な基準がないため、少々使い勝手が悪くなっています。
複数の検査を比較するのではなく、1つの検査について、その良し・悪しを判断するためには、ROC曲線のAUC=0.8という基準と比較すると良いでしょう。
参考文献
[1] Davis J, Goadrich M. The Relationship Between Precision-Recall and ROC Curves. 2006

Comments