概要
筆者の専門はデータサイエンスです。
しかし筆者は一時期、データサイエンティストはExcelとPythonをパチパチやって格好良いことを言うだけの虚業だと思い悩んだことがあり、なんなら今でも少しそう思っている節があります。
普段データを解析して飯を食っていますし、企業研修等でデータサイエンス技術を多くの人にお伝えしてきましたが、「ビジネス現場での応用」なんかをフワッと考えていると、「あれ?やっぱり虚業なんじゃない?」という考えが頭をよぎります。
多分、実際にモノを生み出していないという点が問題なんだと思います。
ところがある時「シュリクマー関数」に出会い、データサイエンスが世界に貢献するための、大切な目的の1つに気づけたように感じました。
その目的とは、
「取得が難しい情報を、取得が簡単な情報で置き換える」
ことです。
この記事を読むことで、「データを解析して求めるべきものとは何か?」についての1つの指針を得られるかもしれません。
シュリクマー関数との出会い
あなたは以下の公式を知っていますか?
$$S=-8.245+6.807H+7.073FFC$$
この式では、肩の高さ \(H\) と前足の周囲長 \(FFC\) (Fore-footpad circumference)から、インドゾウの体表面積 \(S\) を求めています。
つまり、インドゾウの体表面積を求めたいときに便利です。
この公式は、ケラーラ農業大学(インド)のK.P.スリークマル博士とG.ニーマラン博士によって発見され、その功績をもって両氏は2002年のイグノーベル賞を受賞しました。
「どうして体表面積を求める必要があるんですか?」
実は生物の体表面積は、薬の投与量を決める際に非常に重要になります。
なぜならば、体表面積は「体の大きさ」さらに言うと「代謝能力」の指標となり、これに基づいて十分な効果が得られるとともに、副作用がひどくなりすぎない薬量を決定する必要があるためです。
具体的には、体表面積は循環血液量や腎臓の濾過量と相関すると言われています。
人間の場合だと、抗がん剤の「TS-1」等が体表面積によって投与量が決められている薬の例です。
そういうわけで、実は人間版の体表面積決定公式もあります。
- デュポア式
$$(体表面積)=(身長)^{0.725}\times(体重)^{0.425}\times 0.007184$$
- 新谷式
$$(体表面積)=(身長)^{0.725}\times(体重)^{0.425}\times 0.007358$$
- 藤本式
$$(体表面積)=(身長)^{0.663}\times(体重)^{0.444}\times 0.008883$$
以上から、インドゾウ(1986年から絶滅危惧種に指定されている)の健康を守る上で、体表面積という情報は非常に重要であることがわかってもらえたと思います。
取得が難しい情報を、取得が簡単な情報で置き換える
取得が難しい情報
データサイエンスばかりをしていると、今扱っている「データ」はどこから来たのかを忘れてしまいます。
データは誰かが取得するものですが、基本的には、そのために何らかのセンサが必要です。
そのため、測定が難しい対象向けのセンサを開発したり、センサの精度を向上させたりしている人々は、確実に世界に貢献していると言えるでしょう。
「測定が難しい対象」といえば、今回の体表面積のセンサを作るのは相当難しいと思います。
そして作るだけでなく、運用も問題になります(背中の計測はなんとかなるかもしれませんが、おなかや足の裏を測る際には、ゾウさんには寝てもらう必要がありそうです)。
よって、体表面積は取得が難しい情報と言えます。
取得が簡単な情報
対して、肩の高さや前足の周囲長はどうでしょうか?
これらは巻き尺を1回ずつ当てれば測定できます。
つまり、肩の高さや前足の周囲長は取得が簡単な情報です。
シュリクマー関数がやったこと
シュリクマー関数は、これらをイコールでつないで、取得が難しい情報を取得が簡単な情報に変換しました。
つまり、体表面積を巻き尺2回で測定できるようにしてしまったのです。
そして、実はこの公式は非常に精度が良いことが知られており、論文中の図によると
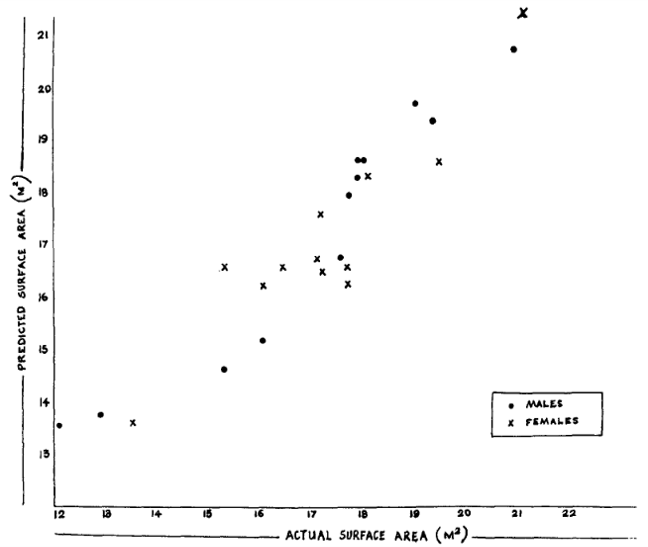
Sreekumar & Nirmalan (1990)[1]より引用
左辺・右辺の値が(インドゾウの性別によらず)きれいな一直線上に並んでいることがわかります。
これはもはや、体表面積の測定器を作ってしまったと言っても過言ではありません。
まとめ
以上を教訓としてまとめると、次のようになります。
- データサイエンティストは、取得が困難な情報を、取得が簡単な情報で置き換えることを目指すべし
- 1.ができたとき、すごいセンサを作ったのと同等の貢献ができる
これに気付けたとき、データサイエンティストという仕事に少し自信が持てた気がしました。
それまでは「データの海から宝物を探す(笑)」みたいな漠然としたことを言っていましたが、上の法則に気付けたことで、データサイエンスにおける方針が立ちやすくなったと思います。
…
なお、筆者はその後「だからといってモノを作るのをやめる理由にはならねぇよなぁ?」と思い、艮電算術研究所では組込みRustを猛プッシュしていくことになりました。

とはいえ、やはり技術的に未熟な部分は多いので、「実装が困難な部分」を「実装が簡単な部分」で置き換えて経験不足をカバーするような立ち回りを心掛けています。
その点、データサイエンスで学んだことが生きているのかもしれません。
以上、雑記でした。
参考文献
[1] K. P. Sreekumar & G. Nirmalan. Estimation of the total surface area in Indian elephants (Elephas maximus indicus). Veterinary Research Communications volume 14, pages 5–17 (1990).



Comments