超幾何分布に基づく集合の類似度指標

Index

概要
表記法
導入：Jaccard係数
問題設定
類似度指標の設計
超幾何分布への変形
指標の計算
活用例
1. 問題
2. 解答

概要

２集合の類似度を測る指標として、Jaccard係数などの手法が知られている。

しかし、２集合の要素となりうる全要素の数と２集合の要素数が所与の場合には、これらの値に依存して、２集合が共通要素を持つ確率が大きく変動する。

この変動を補正するため、この記事では、確率分布を用いた２集合の測定法について提案し、さらにその確率分布が超幾何分布と等しくなることを示す。

この指標は確率分布に基づいているため、「有意に」類似度が高いことも表現可能である。

最後に、Pythonによる実装例も示す。

表記法

$|A|$ は集合 $A$ の要素数を表す。

導入：Jaccard係数

２集合 $A, B$ の類似度を測る指標としてJaccard係数が有名であり

$$J=\frac{|A\cap B|}{|A\cup B|}$$

として定義される。

これは、共通要素数を類似度の基準としつつ、それを集合のサイズで補正した指標である。

このように、集合の類似度指標には、その集合（と共通部分）が生じる状況に合わせて適宜補正を加える必要がある。

問題設定

ここで、特殊な状況として、２集合 $A, B$ の要素が、全体集合 $U$ から選ばれており、それぞれの要素数が決まっている場合を考えてみる。

例えば、

$$U=\{0,1,2,3,4,5,6,7\}$$

とする。

ここで、 $|A|=1, |B|=2$ のようなケースを考えると、これらの集合が共通要素を持つ可能性は非常に小さい。

逆に、 $|A|=6, |B|=5$ のような場合、これらの集合が共通要素を持たない方がおかしい。（具体的には、２集合は少なくとも３つの共通要素を持つ）

したがって、共通要素数を類似度の基準とする場合、それは全体集合と２集合それぞれの要素数によって補正される必要がある。

類似度指標の設計

$|U|=N, |A|=n, |B|=m$ とおく。

$|A\cap B|=x$ となる確率を $P(x)$ とおくと

$N$ 個から $n$ 個を取り出す方法は ${}_N\mathrm{C}_n$ 通り
$N$ 個から $m$ 個を取り出す方法は ${}_N\mathrm{C}_m$ 通り
$N$ 個から $x$ 個を取り出す方法は ${}_N\mathrm{C}_x$ 通り
共通要素以外の $N-x$ 個から、 $A$ の残り $n-x$ 個を取り出す方法は ${}_{N-x}\mathrm{C}_{n-x}$ 通り
$A$ の要素以外の $N-n$ 個から、 $B$ の残り $m-x$ 個を取り出す方法は ${}_{N-n}\mathrm{C}_{m-x}$ 通り

より、

$$P(x)=\frac{{}_N\mathrm{C}_x\cdot{}_{N-x}\mathrm{C}_{n-x}\cdot{}_{N-n}\mathrm{C}_{m-x}}{{}_N\mathrm{C}_n\cdot{}_N\mathrm{C}_m}\tag{1}$$

となる。ここで、 $x$ が取りうる値の範囲は

$$\max{(0, n+m-N)}\leq x \leq \min{(n, m)}$$

である。この範囲にあるすべての $x$ について $P(x)$ を計算することで、その分布がわかる。

その分布を用いると、実際の共通要素数が分布内で「有意に」大きい・小さいかを判別することができる。

超幾何分布への変形

上記の指標 $P(x)$ は超幾何分布

$$P(x|N,m,n)=\frac{\binom{m}{x}\binom{N-m}{n-x}}{\binom{N}{n}}$$

に等しい。

以下、導出を行う。式 $(1)$ を書き下して

$$P(x)=\frac{N!(N-x)!(N-n)!n!(N-n)!m!(N-m)!}{x!(N-x)!(n-x)!(N-n)!(m-x)!(N-n-m+x)!N!N!}$$

$$=\frac{(N-n)!n!m!(N-m)!}{x!(n-x)!(m-x)!(N-n-m+x)!N!}$$

$$=\frac{m!}{x!(m-x)!}\frac{(N-m)!}{(n-x)!(N-n-m+x)!}\frac{(N-n)!n!}{N!}$$

$$=\frac{\binom{m}{x}\binom{N-m}{n-x}}{\binom{N}{n}}$$

と変形される。

これは意味の上からも導出される。

先に $B$ の要素を取り出して、これを「成功」とする
全体 $N$ 個から $A$ の要素を取り出す方法は ${}_N\mathrm{C}_n$ 通り
$B$ （「成功」）の中から $x$ 個取り出す方法は ${}_m\mathrm{C}_x$ 通り
$U\cap\overline{B}$ （「失敗」）の中から $n-x$ 個取り出す方法は ${}_{N-m}\mathrm{C}_{n-x}$ 通り

指標の計算

指標が超幾何分布にしたがうことが示されたので、計算に様々な統計ライブラリや先行研究の知見を活用することができる。

特に、当サイトでは超幾何分布を漸化式的に求める方法について提案している。

超幾何分布の効率的数値計算法

概要超幾何分布の確率質量関数は $$P(x|N,K,n)=\frac{\binom{K}{x}\binom{N-K}{n-x}}{\binom{N}{n}}$$ であり、これをすべての $x$ について計算することによって累積分布関数...

また、 $N$ が十分大きい場合は二項分布に近似して計算を高速化することもできる。

（参考）

超幾何分布の性質と近似―二項分布とポワソン分布との関係

概要この記事では、超幾何分布の性質について簡単に説明した後、特定の条件下で、超幾何分布が二項分布、そしてポワソン分布に近似されることを示す。超幾何分布全 $N$ 個のうち、 $K$ 個が「成功」（赤玉・白玉などで考えて良い）で...

活用例

問題

$|A|=30, |B|=40$ である集合 $A, B$ が存在する。それぞれの要素は $|U|=100$ となる集合 $U$ から抽出されていることが分かっている。 $A, B$ に共通する要素が何個以上があれば、これらの集合は「有意に」似ていると言うことができるだろうか？

解答

import numpy as np

N = 100
m = 40
n = 30

if n <= m:
    pmf = [np.prod([(N-m-i) / (N-i) for i in range(n)])]
else:
    pmf = [np.prod([(N-n-i) / (N-i) for i in range(m)])]
for i in range(min(n, m)):
    pmf.append(pmf[i] * (m-i) * (n-i) / ((i+1) * (N-m-n+i+1)))
cdf = np.cumsum(pmf)  

plt.plot(np.arange(min(n, m)+1), cdf, label="CDF")
plt.hlines(y=0.95, xmin=0, xmax=min(n, m), color="C1", linestyle="--", label="p=0.95", alpha=0.6)
plt.vlines(x=15, ymin=0, ymax=1, color="C2", linestyle="--", label="x=15, p={:.3f}".format(cdf[15]), alpha=0.6)
plt.vlines(x=16, ymin=0, ymax=1, color="C3", linestyle="--", label="x=16, p={:.3f}".format(cdf[16]), alpha=0.6)
plt.legend(loc="lower right")
plt.title("CDF of hypergeom")
plt.xlabel("x")
plt.ylabel("p")
plt.show()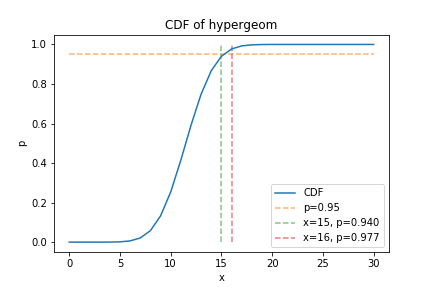

超幾何分布 $P(x|100,40,30)$ の累積分布関数を求めると上図のようになり、 $x=16$ のとき $p\risingdotseq0.977$ となって上位５％点を超える。

すなわち、 $x\geq16$ であれば、上記の意味で「有意に」 $A, B$ は似ているといえる。