概要
この記事では、2集合の類似度を測る指標として、Jaccard係数、Dice係数、Simpson係数、Kendall相関係数、超幾何分布の累積分布に基づく指標を説明する。
一般的な指標は前3者であるが、ここでは、集合に含まれうる要素の全体集合がわかっている場合にはKendall相関係数を、さらに2集合の要素数が固定されている場合には超幾何分布の累積分布を用いることを提案する。
また、各指標の具体的な計算例についても記載した。
これらの指標はバイオインフォマティクスに応用することができ、例えば各疾患で強く発現する遺伝子(バイオマーカー)の組や、神経活動アンサンブルを構成する神経細胞の組の類似度を表現する際に役立つ。
(この記事は「バイオインフォマティクス Advent Calendar 2021|2日目に登録されています)

例題
以下、各指標を用いて、以下の2集合の組 \((A,B)\) と \((C,D)\) の類似度を計算する。
ただし、各集合の要素は全体集合
$$U=\{a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z\}$$
$$|U|=26$$
から得られているものとし、2集合 \(X,Y\) の類似度を \(S(X,Y)\) で表す。
例1
$$A=\{a,b,c,d,e,f,g,h,i,j,k,l,m\}$$
$$B=\{a,d,g,j,m,p,s,v,y\}$$
例2
$$C=\{a,b,c,d\}$$
$$D=\{a,b\}$$
一般の場合
Jaccard係数
定義
$$S(X, Y)=\frac{|X\cap Y|}{|X\cup Y|}$$
性質
\(X\) または \(Y\) に含まれている要素のうち、 \(X, Y\) に共通する要素の割合を表現する。
値域は \([0,1]\) であり、 \(1\) に近いほど類似度が高い。
計算例
$$S(A,B)=\frac{5}{17}\fallingdotseq 0.29$$
$$S(C,D)=\frac{2}{4}=0.5$$
Dice係数
定義
$$S(X, Y)=\frac{|X\cap Y|}{\frac{|X|+|Y|}{2}}=\frac{2|X\cap Y|}{|X|+|Y|}$$
性質
Jaccard係数の分母を、 \(X, Y\) の要素数の平均に変えるとDice係数になる。
値域は \([0,1]\) であり、 \(1\) に近いほど類似度が高い。
計算例
$$S(A,B)=\frac{2\cdot 5}{13+9}=\frac{10}{22}\fallingdotseq 0.45$$
$$S(C,D)=\frac{2\cdot 2}{4+2}=\frac{4}{6}\fallingdotseq 0.67$$
Simpson係数
定義
$$S(X, Y)=\frac{|X\cap Y|}{\min(|X|,|Y|)}$$
性質
\(X, Y\) のうち、小さい方の要素数を分母とすることによって、集合のサイズに差がある場合の偏りを補正する。
値域は \([0,1]\) であり、 \(1\) に近いほど類似度が高い。
また、 \(X\) が \(Y\) に完全に含まれている場合(例2:またはその逆)、Simpson係数は \(1\) (=完全一致)となるが、Jaccard係数とDice係数はそうならない。
計算例
$$S(A,B)=\frac{5}{9}\fallingdotseq 0.56$$
$$S(C,D)=\frac{2}{2}=1$$
類似度指標の補正
Jaccard係数、Dice係数、Simpson係数はすべて \(0\) を最も似ていない、 \(1\) を完全一致として表現しているが、以下の状況によって、値が上下しやすくなる。
- 各集合がとりうる要素が属する全体集合
- 各集合の要素数
例えば、以下のケースでのJaccard係数を考える。
- ケース1
$$U_{EF}=\{1,2,3,4,5,\ldots,1000000\}$$
$$E=\{1,2,3,4\}, F=\{2,3,4,5\}$$
- ケース2
$$U_{GH}=\{1,2,3,4,5\}$$
$$G=\{1,2,3,4\}, H=\{2,3,4,5\}$$
\(E=G, F=H\) より、
$$S(E,F)=S(G,H)=\frac{3}{5}=0.6$$
となるが、この \(0.6\) という値は等価ではない。
なぜならば、百万も要素がある中から \(E, F\) のような取られ方をしてくるのは奇跡的と言ってもよい。
逆に、5つしかない要素から \(G,H\) のような取られ方をするのは極めて自然である。さらに、 \(|G|=|H|=4\) が固定されている場合、Jaccard係数は \(0.6\) 以下になり得ない。
よって実用的には、要素の全体集合と各集合の要素数のバランスから、値を補正できる類似度指標が必要になる場合がある。
ここでは、
- 要素の全体集合が既知である場合
- 要素の全体集合が既知、かつ、各集合の要素数が固定されている場合
の類似度指標について提案する。
ここで提案する手法は、共に確率分布を活用したものなので、便宜的に「有意に」類似した集合を主張することも可能となる。
要素の全体集合が既知である場合
Kendall相関係数
定義と性質
全体集合と同じ長さの数列を用意し、各集合に含まれる要素に対応する位置を \(1\) 、そうでない位置を \(0\) とする。
この数列のKendall相関係数を求めると、値域は \([-1,1]\) となり、 \(1\) が完全一致、 \(-1\) が完全不一致(逆相関)となる。
Kendall相関係数については、以下を参照。

さらに、計算過程で
$$z_B=\frac{K^+-K^-}{\sqrt{v}}$$
を計算すると、この値は標準正規分布 \(\mathcal{N}(0,1)\) にしたがうことが知られている。(各変数の定義については以下を参照)
すなわち、標準正規分布の累積分布関数を \(\Phi(\cdot)\) とすると、 \(\Phi(z_B)\) は \([0,1]\) の値域を取り、 \(1\) に近いほど類似度が高いといえる。
効率的な計算方法
Kendall相関係数の単純実装の計算量は \(O(N^2)\) であるが、平衡二分木を用いると \(O(N\log N)\) となることが知られている。
また、数列の要素が \(0, 1\) しかない場合は \(O(N)\) で計算できる。詳細は以下を参照。

計算例
\(l(X)\) を集合 \(X\) の要素に基づいて作成された数列とする。
例1について、
$$l(A)=[1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0]$$
$$l(B)=[1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0]$$
より、
$$K^+=5\cdot 9=45$$
$$K^-=8\cdot 4=32$$
$$v\fallingdotseq 1034.277$$
なので
$$z_B=\frac{45-32}{\sqrt{1034.277}}\fallingdotseq\frac{13}{32.16}\fallingdotseq 0.404$$
したがって
$$S(A,B)=\Phi(0.404)\fallingdotseq 0.66$$
例2について、
$$l(A)=[1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]$$
$$l(B)=[1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]$$
より、
$$K^+=2\cdot 22=44$$
$$K^-=2\cdot 0=0$$
$$v\fallingdotseq 169.000$$
なので
$$z_B=\frac{44-0}{\sqrt{169}}=\frac{44}{13}\fallingdotseq 3.385$$
したがって
$$S(C,D)=\Phi(3.385)\fallingdotseq 0.9996 $$
要素の全体集合が既知、かつ、各集合の要素数が固定されている場合
超幾何分布の累積分布
定義と性質
$$|U|=N,|X|=n,|Y|=m$$
のとき、 \(X, Y\) の共通要素数 \(|X\cap Y|=x\) の値は超幾何分布にしたがう。
すなわち
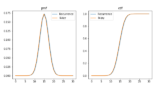
$$P(|X\cap Y|=x)=\frac{\binom{m}{x}\binom{N-m}{n-x}}{\binom{N}{n}}$$
となる。この辺りの議論については以下を参照。

ここで累積分布 \(P(|X\cap Y|\leq x)\) を考えると、値域は \([0, 1]\) であり、 \(1\) に近いほど類似度が高いといえる。
効率的な計算方法
超幾何分布は二項係数を含むため、累積分布を求める際の計算量が非常に多くなる。
しかし、 \(P(X=x+1)\) の値は \(P(X=x)\) を用いて漸化式的に計算することができ、重複する計算を削減可能である。詳しくは以下を参照。
計算例
$$P(|A\cap B|=0)=\frac{\binom{9}{0}\binom{26-9}{13-0}}{\binom{26}{13}}\fallingdotseq 0.00023$$
$$P(|A\cap B|=1)=\frac{(9-0)(13-0)}{(0+1)(26-9-13+0+1)}P(|A\cap B|=0)\fallingdotseq 0.00535$$
$$P(|A\cap B|=2)=\frac{(9-1)(13-1)}{(1+1)(26-9-13+1+1)}P(|A\cap B|=1)\fallingdotseq 0.04284$$
$$P(|A\cap B|=3)=\frac{(9-2)(13-2)}{(2+1)(26-9-13+2+1)}P(|A\cap B|=2)\fallingdotseq 0.15707$$
$$P(|A\cap B|=4)=\frac{(9-3)(13-3)}{(3+1)(26-9-13+3+1)}P(|A\cap B|=3)\fallingdotseq 0.294508$$
$$P(|A\cap B|=5)=\frac{(9-4)(13-4)}{(4+1)(26-9-13+4+1)}P(|A\cap B|=4)=0.294508$$
より、
$$S(A,B)=P(|A\cap B|\leq 5)$$
$$=0.00023+0.00535+0.04284+0.15707+0.294508+0.294508$$
$$\fallingdotseq 0.79$$
例2については、 \(|C|=4,|D|=2\) のとき、 \(0\leq|C\cap D|\leq 2\) より、
$$S(C, D)=1$$
まとめ
バイオインフォマティクス応用をはじめ、2つグループの類似度を測りたいケースは少なくない。
その際、Jaccard係数、Dice係数、Simpson係数のような一般的な指標も使えるが、これらの値はデータが生じた背景に依存して変化しやすいため比較が難しい。
要素の全体集合が既知であるような場合には、確率分布に基づいたアプローチが可能であり、ここではKendall相関係数と超幾何分布の累積分布を紹介した。
確率分布に基づく指標は、累積分布の値から、便宜上「類似度が『有意に』大きい」ということができるかもしれない。


Comments