相互に接する円をコンパスでいくつか描画することにより、正五角形を作図する方法があると知ったのでここに記録する。
コンパスを使って正五角形を描く
手順1
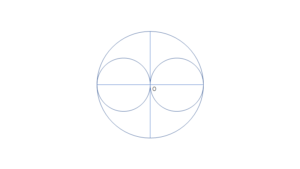
点Oを中心とする円(円Oとする)の中に、半径が半分の円が2つ入るように作図する。(十字線は補助)
手順2
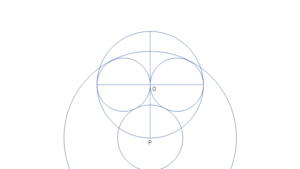
十字線のうち、垂直な方と円Oの交点(点Pとする)を中心とし、内部の2つの円に接する円を2つ描画する(大きい円を円Po、小さい円を円Piとする)。
手順3
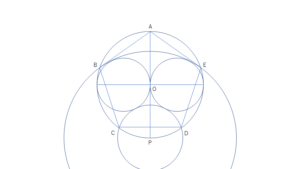
点Pと反対側にある垂直線と円Oの交点(点Aとする)、円Poと円Oの2つの交点(点B, Eとする)、円Piと円Oの2つの交点(点C, Dとする)を直線で結ぶと、五角形ABCDEは正五角形となる。
正五角形であることの証明
各円の半径の計算
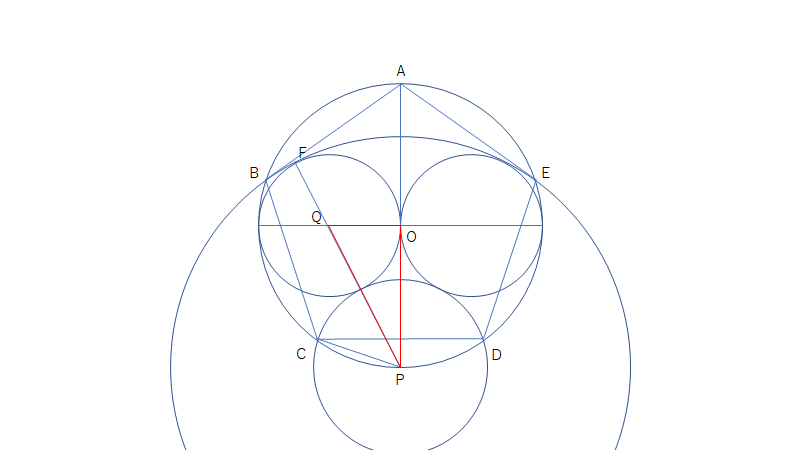
<手順1>で描いた2つの円の片方を円Qとし、その半径を \(r\) とおく。点Pから点Qに線を引くと、その線は円Qと円Poの交点、円Qと円Piの交点の双方を通る。
△OPQに注目すると \(OP=2r, OQ=r\) であり、 \(\angle POQ=90^\circ\) より三平方の定理から、
$$PQ=\sqrt{(2r)^2+r^2}=\sqrt{5}r$$
となる。ここで、 \(PQ\) は円Piと円Qの半径の和に等しいため、円Piの半径は \(\sqrt{5}r-r=(\sqrt{5}-1)r\) となる。
また、 \(PF\) は円Piの半径と円Qの直径の和に等しいため、 \(PF=(\sqrt{5}-1)r+2r=(\sqrt{5}+1)r\) である。
辺AB(EA)の計算
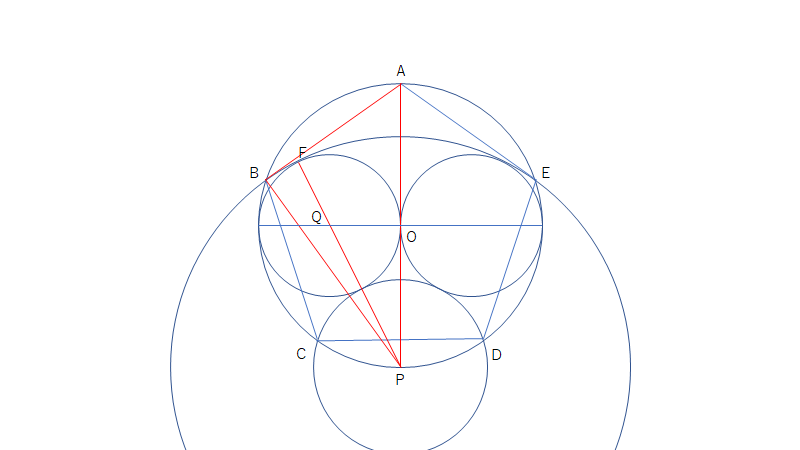
点Bと点Pを結ぶと、 \(PB\) と \(PF\) はともに円Poの半径であるため、 \(PB=PF=(\sqrt{5}+1)r\) となる。次に△ABPに注目すると、 \(\angle ABP=90^\circ\) (∵ \(AP\) は円Oの直径であり、点Bも円O上の点:タレスの定理)より、三平方の定理から、
$$AB=\sqrt{(4r)^2-((\sqrt{5}+1)r)^2}$$
$$AB=\sqrt{16r^2-(6+2\sqrt{5})r^2}$$
$$AB=r\sqrt{10-2\sqrt{5}}$$
が求まる。対称形より、同様の手順により \(EA=r\sqrt{10-2\sqrt{5}}\) となる。
辺CDの計算
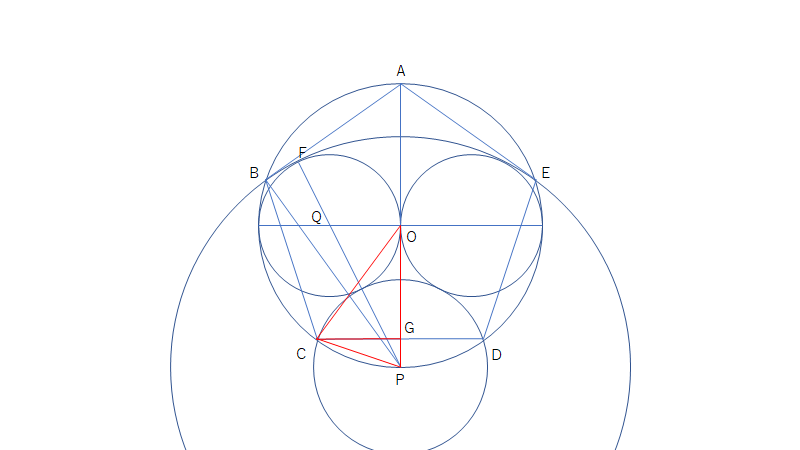
今度は△OCGと△PCGに注目する。 \(OP=OC=2r, PC=(\sqrt{5}-1)r\) であり、 \(GP=x, CG=y\) とおくと、それぞれの直角三角形についての三平方の定理から、
$$\begin{eqnarray} \left\{ \begin{array}{l} (2r)^2=(2r-x)^2+y^2 \\ \{(\sqrt{5}-1)r\}^2=x^2+y^2 \end{array} \right.\end{eqnarray}$$
これを解いて、
$$\begin{eqnarray} \left\{ \begin{array}{l} 4r^2=4r^2-4rx+x^2+y^2 \\ (6-2\sqrt{5})r^2=x^2+y^2 \end{array} \right.\end{eqnarray}$$
$$\begin{eqnarray} \left\{ \begin{array}{l} 4rx=x^2+y^2 \\ (6-2\sqrt{5})r^2=x^2+y^2 \end{array} \right.\end{eqnarray}$$
2式の辺々を引いて、
$$4rx-(6-2\sqrt{5})r^2=0$$
$$r\{2x-(3-\sqrt{5})r\}=0$$
\(r\not=0\) より、 \(x=\frac{3-\sqrt{5}}{2}r\) である。よって、
$$y=\sqrt{(6-2\sqrt{5})r^2-x^2}$$
$$y=\sqrt{(6-2\sqrt{5})r^2-(\frac{3-\sqrt{5}}{2}r)^2}$$
$$y=\sqrt{(6-2\sqrt{5})r^2-\frac{14-6\sqrt{5}}{4}r^2}$$
$$y=\frac{\sqrt{(24-8\sqrt{5})r^2-(14-6\sqrt{5})r^2}}{2}$$
$$y=\frac{r}{2}\sqrt{10-2\sqrt{5}}$$
以上より、 \(GP=x=\frac{3-\sqrt{5}}{2}r, CG=y=\frac{r}{2}\sqrt{10-2\sqrt{5}}\) であり、 \(CD=2CG=r\sqrt{10-2\sqrt{5}}\) が求まる。
辺BC(DE)の計算
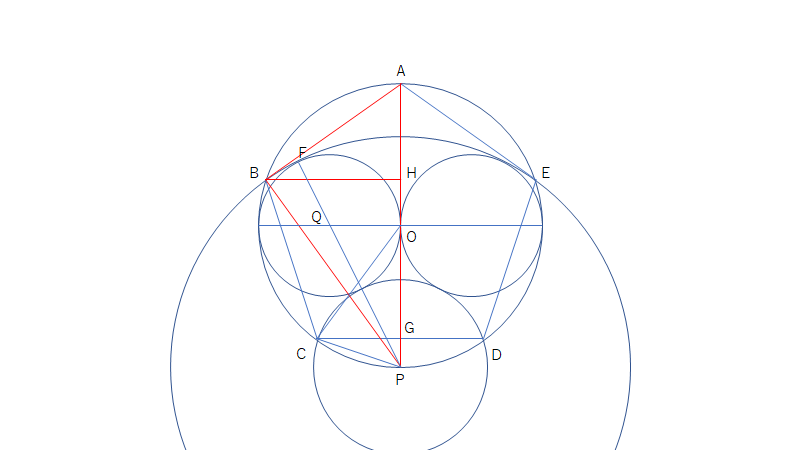
次に点Bから \(AP\) に垂線を下ろし、その足を点Hとする。ここで、△PABと△PBHに注目すると、 \(\angle APB\) と \(\angle BPH\) は共通で \(\angle PAB=\angle PBH=90^\circ\) より、両者は相似である。よって、
$$AB:BH = PA:PB $$
$$BH=\frac{AB\cdot PB}{PA}$$
$$BH=\frac{r\sqrt{10-2\sqrt{5}} \cdot (\sqrt{5}+1)r}{4r}$$
$$BH=\frac{(\sqrt{5}+1)\sqrt{10-2\sqrt{5}}}{4}r$$
ここで、
$$(\sqrt{5}+1)^2=6+2\sqrt{5}$$
より、
$$\sqrt{5}+1=\sqrt{6+2\sqrt{5}}$$
なので、
$$BH=\frac{\sqrt{6+2\sqrt{5}}\sqrt{10-2\sqrt{5}}}{4}r$$
$$BH=\frac{\sqrt{(6+2\sqrt{5})(10-2\sqrt{5})}}{4}r$$
$$BH=\frac{\sqrt{(6+2\sqrt{5})(10-2\sqrt{5})}}{4}r$$
$$BH=\frac{\sqrt{40+8\sqrt{5}}}{4}r$$
$$BH=\frac{2\sqrt{10+2\sqrt{5}}}{4}r=\frac{r}{2}\sqrt{10+2\sqrt{5}}$$
また、△PBHにおける三平方の定理から、
$$PH=\sqrt{\{(\sqrt{5}+1)r\}^2-(\frac{\sqrt{10+2\sqrt{5}}}{2}r)^2}$$
$$PH=\sqrt{(6+2\sqrt{5})r^2-\frac{10+2\sqrt{5}}{4}r^2}$$
$$PH=r\sqrt{\frac{4(6+2\sqrt{5})}{4}-\frac{10+2\sqrt{5}}{4}}$$
$$PH=\frac{r}{2}\sqrt{4(6+2\sqrt{5})-(10+2\sqrt{5})}$$
$$PH=\frac{r}{2}\sqrt{14+6\sqrt{5}}$$
$$PH=\frac{r}{2}\sqrt{14+2\sqrt{45}}=\frac{3+\sqrt{5}}{2}r$$
さらに、 \(HG=PH-GP\) より、
$$HG=\frac{3+\sqrt{5}}{2}r-\frac{3-\sqrt{5}}{2}r$$
$$HG=\sqrt{5}r$$
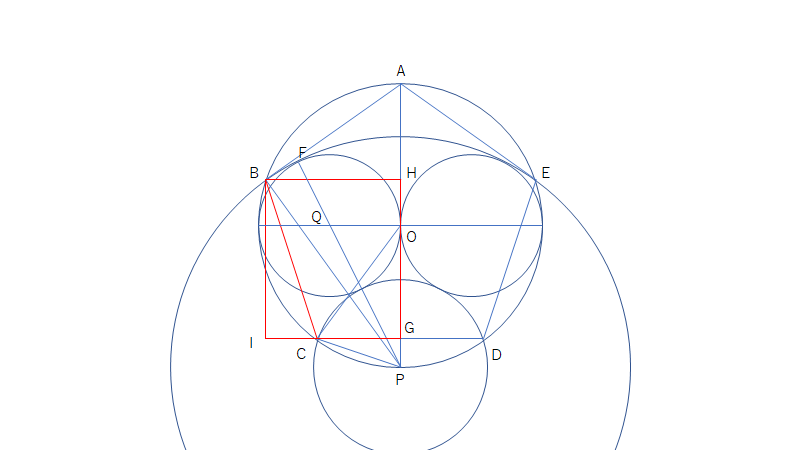
最後に、 \(CD\) の延長線上に点Bから下ろした垂線の足をIとすると、 \(IG=BH=\frac{r}{2}\sqrt{10+2\sqrt{5}}, BI=HG=\sqrt{5}r\) であり、 \(IC=IG-CG\) より、
$$IC=\frac{r}{2}\sqrt{10+2\sqrt{5}}-\frac{r}{2}\sqrt{10-2\sqrt{5}}$$
$$IC=\frac{r}{2}(\sqrt{10+2\sqrt{5}}-\sqrt{10-2\sqrt{5}})$$
よって、△BCIについての三平方の定理から、
$$BC=\sqrt{(\frac{r}{2}(\sqrt{10+2\sqrt{5}}-\sqrt{10-2\sqrt{5}}) )^2+(\sqrt{5}r)^2}$$
$$BC=\sqrt{\frac{r^2}{4}((10+2\sqrt{5})+(10-2\sqrt{5})-2\sqrt{(10+2\sqrt{5})(10-2\sqrt{5})})+5r^2}$$
$$BC=\sqrt{\frac{r^2}{4}(20-2\sqrt{100-20})+5r^2}$$
$$BC=\frac{r}{2}\sqrt{(20-2\sqrt{80})+20}$$
$$BC=\frac{r}{2}\sqrt{40-8\sqrt{5}}=r\sqrt{10-2\sqrt{5}}$$
が求まる。対称形より、同様の手順により \(DE=r\sqrt{10-2\sqrt{5}}\) となる。
結論
以上より、 \(AB=BC=CD=DE=EA=r\sqrt{10-2\sqrt{5}}\) となるので、ABCDEは正五角形である。

Comments