Brian Greenhill, Michael D. Ward, Audrey Sacks.
"The Separation Plot: A New Visual Method for Evaluating the Fit of Binary Models"
American Journal of Political Science 2011; 55(4): pp. 990–1002
Contents
The Separation Plot
モデルの予測能力を評価するための新しい方法として、「The Separation Plot」を開発した。この手法は、より視覚的に結果を示すことを目的とし、従来の数字の羅列よりも直感的なモデルの性能評価が可能となる。
「The Separation Plot」の主なコンセプトは以下の通りである。
(例)表のようなデータが得られているとする
| Data | 実際のラベル(y) | 予測確率(p) |
| A | 0 | 0.774 |
| B | 0 | 0.364 |
| C | 1 | 0.997 |
| D | 0 | 0.728 |
| E | 1 | 0.961 |
| F | 1 | 0.442 |
このような表は、データセットX = [x1, x2, x3, ...]から得られるものである。個々のデータは特定のラベルy(y = 0 または 1。0 or 1はそれぞれ陰性or陽性、平和or戦争などを意味する)と対応付けられている。機械学習などのモデルはこのデータを利用し、個々のラベルが1である確率を予測する。その確率がpである。
「The Separation Plot」では、まずこれらのデータをp値に従って並べる(右側ほどpが大きくなる)。
| B | F | D | A | E | C |
実際のラベルが1であるものは赤で表示した。
ここで、このモデルが正確に予測を行うならば、右側に赤、左側に黒の文字が固まるはずである。このように確率p順に並べたデータのラベルが、どのような集まり方をしているかを視覚的に確認することによってモデルの性能を評価する方法が「The Separation Plot」である。
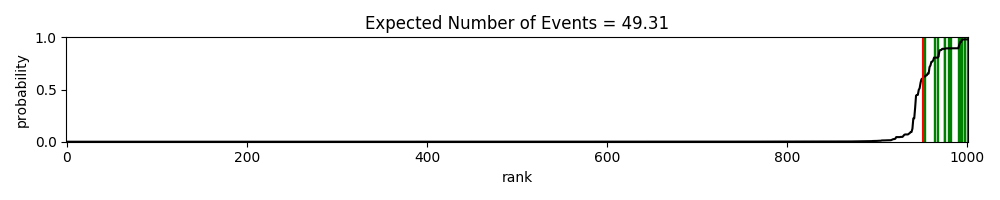
上図が実際の「The Separation Plot」である。この図では約1000個のデータに対し予測を行った。
緑線(本当は長方形。データ数が多いので線に見える)は実際のラベルが1のデータを示す。それ以外のスペースは空白ではなく、白線(長方形)でラベル0のデータを示している。黒線は各データにおける予測確率pの値を示しており、ここから右に行くほどpが大きくなることがわかる。
赤線は「Expected Number of Events(ENoE)」という指標を示し、これは予測確率pの総和のことである。今回は ENoE = 49.31 であるため、右から49.31番目のところに線が引かれている。もしモデルが完全な予測(ラベル1のデータに対してはp=1.000, ラベル0のデータに対してはp=0.000を出力する)ならば、「The Separation Plot」は右に緑線が固まり、その隣に赤線が引かれ、さらにその隣から左端まで白線が並ぶはずである。赤線(ENoE)は、こうした理想形からどれほど実際の結果が離れているかを視覚的に示している。
上図では緑と白が綺麗に分離しており、かなり高い予測性能を示していると言える。p=0.600くらいのところを閾値とすれば、わずかな偽陽性のもと、陽性例を完全に分離できることからも、この予測が優れていることがわかるだろう。
逆に、緑と白が完全にランダムに並んだ場合は予測性能が低いことがわかる。(緑が左側に集まった場合は「逆に」性能がよい。モデルの作り方は間違っているが、結果をひっくり返せば正しい予測ができる。)
Impressions
本論文ではSupplemental Informationとして、R言語による「The Separation Plot」のコードを提供している。しかし、予測の分野では今後、Pythonがメイン言語となっていくであろう。そこで、わがLab.ではPythonによる「The Separation Plot」のコードを作成した。コードはこちらのページからコピーし、あなたの分析ファイル.pyにimportしてほしい。


Comments