概要
空間内の点をいくつかのグループに分割することを考え、データにK-meansクラスタリングアルゴリズムを適用する。応用例として、MDSを用いて点同士の距離が任意となる場合(直線距離でなく道のりが与えられる等)の最適化手法についても考える。最後に、クラスター同士が均等な大きさとなるような場合の手法についても考える。
なお、当記事のコードはすべてPythonで実装されている。実装したコードは
にJupyter Notebookとしてまとめてある。
動機
2021年2月のすべての土日を使って、総務省主催のGeospatial Hackers Program、すなわち地理空間情報技術を活用したプロダクト開発ハッカソンに技術メンターとして参加した。その際、「災害時の避難所を地図上に表示し、位置・標高・人口等をもとに、最適な給水所の配置計画について考える」というプロジェクトが立った。Pythonの機械学習ライブラリを使えば、給水所のクラスタリングくらいは簡単にできるのではないかと思ったので、ここに手法をまとめることにした。
本文
必要なもの
- Python3 (ver. 3.8 以上が望ましい)
加えて、以下のライブラリを必要とする。pip等を使ってインストールしてほしい。
- numpy
- matplotlib
- scikit-learn
また、以下のようなデータ分析は
- Jupyter Notebook
上で行うと便利である。
ライブラリのインポート
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3DN次元配列を扱うためのnumpy, グラフ表示用のmatplotlibに加え、3D表示用のmpl_toolkitsの必要な機能をインポートする。
ダミーデータの準備
# generate data
cov = np.eye(3)
np.random.seed(42)
c0 = np.random.multivariate_normal([0.0, 0.0, 0.0], cov, size=10)
c1 = np.random.multivariate_normal([2.0, 2.0, 0.0], cov, size=10)
c2 = np.random.multivariate_normal([2.0, 2.0, 3.0], cov, size=10)
data = np.vstack((c0, c1, c2))3つの異なる中心を持つ、3つの塊のデータ点を生成し、これを避難所の位置に見立てる。このとき、c1, c2の中心は平面上では同じ座標を持つが、標高が異なる。
# plot data to 3D space
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(c0[:, 0], c0[:, 1], c0[:, 2])
ax.scatter3D(c1[:, 0], c1[:, 1], c1[:, 2])
ax.scatter3D(c2[:, 0], c2[:, 1], c2[:, 2])
ax.set_title("3D-data")
plt.savefig("3d_data.png")
plt.show()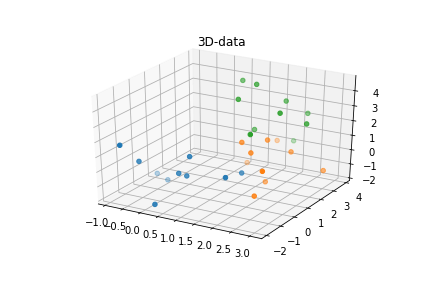
塊ごとに、3次元空間にプロット。
# plot data to 2D plane
plt.scatter(c0[:, 0], c0[:, 1])
plt.scatter(c1[:, 0], c1[:, 1])
plt.scatter(c2[:, 0], c2[:, 1])
plt.title("2D-data")
plt.savefig("2d_data.png")
plt.show()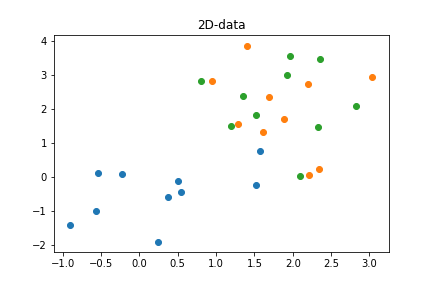
標高の情報を無視して2次元空間にプロットすると、c1, c2の塊は重なっていることがわかる。
2次元データに対する K-means クラスタリング
まずは標高の情報を無視して、2次元のデータでK-meansクラスタリングを試す。
from sklearn.cluster import KMeans機械学習ライブラリのscikit-learnから必要なものをインポートし、
# initialize KMeans class
km = KMeans(n_clusters=3, random_state=42)K-meansクラスタリングのためのクラス(ややこしいが、ここでは構造体のこと)を初期化する。クラスの引数の説明と合わせて、ここでK-meansクラスタリングの原理について解説しておこう。
K-meansクラスタリングでは、最初にK個の点をランダムにばらまく。この点はクラスターの「中心点」と呼ばれる。そして、以下の操作を変化が起こらなくなるまで繰り返す。
- 各データ点を、最も距離が近い中心点のクラスターに割り当てる
- 各クラスターに属するデータ点との距離の合計が最も小さくなる位置に、各中心点を移動する
この結果、各データ点はK個のクラスターにいい感じに分類される。したがって、K-meansクラスタリングを行う際には事前にKの値を決めて置く必要があり、ここではn_clusters=3を指定している。また、初期値はランダムとなるため、再現性を持たせるために乱数シードをrandom_state=42に固定した。
# predict cluster from 2D data
label = km.fit_predict(data[:, :2])これに3つ目の次元を除いたデータを与えることで、それぞれのデータ点がどのクラスターに含まれるかを予測して返してくれる。
# plot result to 2D plane
plt.scatter(data[:, 0][label==0], data[:, 1][label==0])
plt.scatter(data[:, 0][label==1], data[:, 1][label==1])
plt.scatter(data[:, 0][label==2], data[:, 1][label==2])
plt.title("KMeans for 2D-data")
plt.savefig("2d_data_km_2d.png")
plt.show()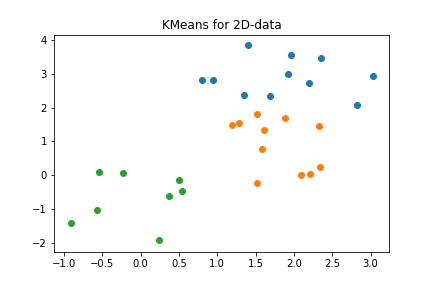
その結果、2次元平面上では綺麗に3つのクラスターに分類されていることがわかる。しかし
# plot result to 3D space
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(data[:, 0][label==0], data[:, 1][label==0], data[:, 2][label==0])
ax.scatter3D(data[:, 0][label==1], data[:, 1][label==1], data[:, 2][label==1])
ax.scatter3D(data[:, 0][label==2], data[:, 1][label==2], data[:, 2][label==2])
ax.set_title("KMeans for 2D-data")
plt.savefig("2d_data_km_3d.png")
plt.show()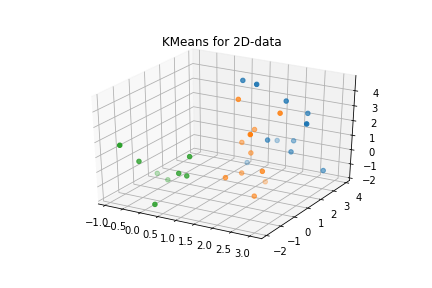
当然といえば当然だが、標高の情報を無視したので、3次元空間上では青とオレンジのクラスターが混ざってしまっている。
3次元データに対する K-means クラスタリング
続いて3次元データに対するK-meansクラスタリングの適用を考える。結論からいうと、K-meansクラスに3次元データを与えれば、3次元空間上でクラスタリングを行ってくれる。
# predict cluster from 3D data
label = km.fit_predict(data)結果をプロットすると
# plot result to 3D space
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(data[:, 0][label==0], data[:, 1][label==0], data[:, 2][label==0])
ax.scatter3D(data[:, 0][label==1], data[:, 1][label==1], data[:, 2][label==1])
ax.scatter3D(data[:, 0][label==2], data[:, 1][label==2], data[:, 2][label==2])
ax.set_title("KMeans for 3D-data")
plt.savefig("3d_data_km.png")
plt.show()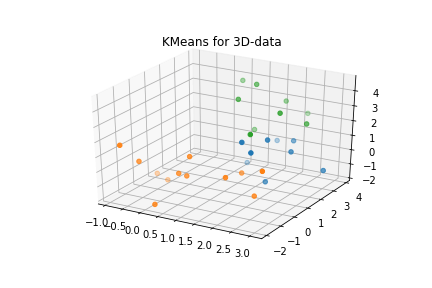
のように、標高も踏まえてのクラスタリングに成功している。
しかし、これではあまり面白くないので、次節ではあえて別の方法でやってみることにしよう。
点の間に任意の距離を設定する場合
地理空間情報を扱う場合、点どうしの距離をユークリッド距離(各座標要素を2乗して足し、平方根を取る。いわゆる一般的な距離)で扱ってよい場合はあまり多くない。各点(今回は避難所)の距離は所要時間として計算した方がより有用であり、それは道路状況や標高に強い影響を受ける。
そのため、各点の座標ではなく、以下の
| A | B | C | ... | |
| A | 0 | A→Bの距離 | A→Cの距離 | ... |
| B | B→Aの距離 | 0 | B→Cの距離 | ... |
| C | C→Aの距離 | C→Bの距離 | 0 | ... |
| ... | ... | ... | ... | ... |
ような距離行列からクラスタリングを行いたい場合がある。
ここではその手法について示す。
注)KMeans の precompute_distances について
距離行列からクラスタリングを行いたい場合、現在(scikit-learn ver. 0.23)はKMeansを初期化する際にprecompute_distances=Trueを指定して、予測の際に距離行列を与えることで実現できる。しかしこの機能は将来的に削除されることが決定しており、現在も非推奨となっている。
そのため長期的に運用する予定のサービスには適用できないし、サポートが不十分かもしれないことを考えると使用すべきではないだろう。
距離行列の計算
「ユークリッド距離を用いない方が良い」と述べたばかりだが、個別に距離を設定するのは面倒であるため、今回の例では3次元ユークリッド距離を用いる。すなわち、3次元空間で計算した距離を用いて、各点を2次元平面上に再配置する。
# calculate distance between points
diff = data.reshape(30, 1, 3) - data.reshape(1, 30, 3)
dist = np.sqrt(np.sum(diff**2, axis=2))本筋からは逸れるので詳細は活用するが、今回の距離行列distは以上のように計算できる。
MDSによる変換
以降の方針としては、距離行列に基づいてデータ点の位置を再配置し、その再配置された点に対してクラスタリングを行うことを考える。この再配置には、多次元尺度構成法(MDS: MultiDimensional Scaling)を用いる。MDSは、距離行列によって表現された距離感を実現するために最適な点の配置を計算するアルゴリズムである。
from sklearn.manifold import MDSまず必要なものをインポートし
# initialize MDS class
mds = MDS(n_components=2, dissimilarity="precomputed", random_state=42)MDSクラスを初期化する。今回は3次元空間上の点を2次元平面上に再配置するためにn_components=2を指定し、事前に距離行列を計算したのでdissimilarity="precomputed"とした。ユークリッド距離を用いる場合、実際はdissimilarity="euclidean"として後の計算の際に生のデータ点を与えれば事足りるのであるが、任意の距離行列に対応するため、今回はこの機能を用いない。
また、scikit-learnでは、MDSもK-meansと同じく「ランダム初期値→繰り返し処理」によって実装されているため、乱数シードをrandom_state=42に固定する。しかし、距離行列が対称である場合には、距離行列の固有値から解析的に変換を行えるので、解の一意性を重視したい場合は
に実装したクラスを使用してみてほしい。
# transform data by MDS
data_mds = mds.fit_transform(dist)MDSクラスにデータを与えることで、3次元空間上のデータ点は2次元平面上に再配置される。実際、塊c0, c1, c2は
# plot MDS data to 2D plane
plt.scatter(data_mds[:10, 0], data_mds[:10, 1])
plt.scatter(data_mds[10:20, 0], data_mds[10:20, 1])
plt.scatter(data_mds[20:30, 0], data_mds[20:30, 1])
plt.title("MDS-data")
plt.savefig("mds_data.png")
plt.show()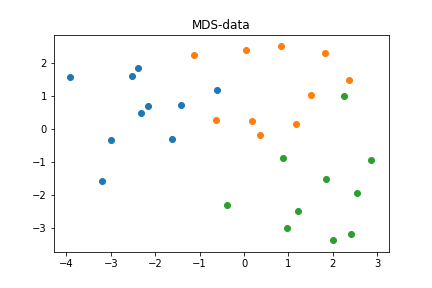
のように視覚上分離して再配置されている。
MDSで変換したデータ点をクラスタリング
# predict cluster from MDS data
label = km.fit_predict(data_mds)再配置されたデータ点をKMeansクラスに与える。
# plot result to 2D plane
plt.scatter(data_mds[:, 0][label==0], data_mds[:, 1][label==0])
plt.scatter(data_mds[:, 0][label==1], data_mds[:, 1][label==1])
plt.scatter(data_mds[:, 0][label==2], data_mds[:, 1][label==2])
plt.title("KMeans for MDS-data")
plt.savefig("mds_data_km_mds.png")
plt.show()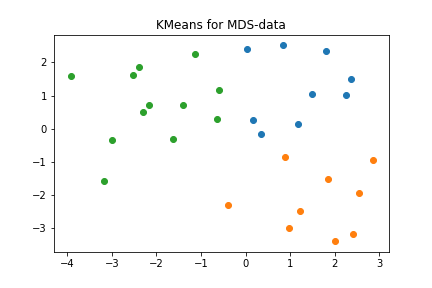
結果は大体予想できるが、上図のように綺麗にクラスタリングされる。ここで、結果のlabelに基づいて、変換前のデータ点を2次元平面上に表示してみよう。
# plot result to 2D plane (2D data)
plt.scatter(data[:, 0][label==0], data[:, 1][label==0])
plt.scatter(data[:, 0][label==1], data[:, 1][label==1])
plt.scatter(data[:, 0][label==2], data[:, 1][label==2])
plt.title("KMeans for MDS-data")
plt.savefig("mds_data_km_2d.png")
plt.show()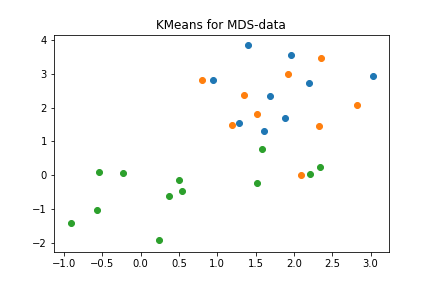
すると非常に入り組んだ構造となり、このようなクラスタリング結果は、もともとのデータ点の配置からは実現されなかったであろうことがわかる。しかし、この結果を図2と比較すると、もとの塊c0, c1, c2と非常に類似していることも見て取れる。実際
# plot result to 3D space
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(data[:, 0][label==0], data[:, 1][label==0], data[:, 2][label==0])
ax.scatter3D(data[:, 0][label==1], data[:, 1][label==1], data[:, 2][label==1])
ax.scatter3D(data[:, 0][label==2], data[:, 1][label==2], data[:, 2][label==2])
ax.set_title("KMeans for MDS-data")
plt.savefig("mds_data_km_3d.png")
plt.show()
plt.show()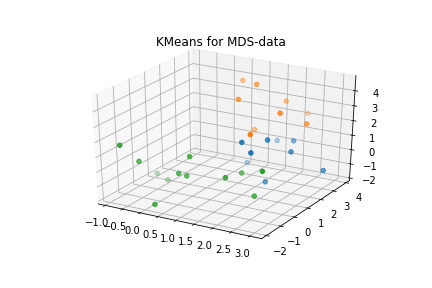
元データの3次元空間でも、正しく分類されている。
クラスターを均等にする場合
この節の内容を実現する関数がパッとは思いつかないため、ここでは考え方のみ述べる。
クラスターに含まれる点の数を可能な限り揃えたい場合
scikit-learnには実装されていない(筆者が見つけられていない)が、次のようなアルゴリズムが提唱されているらしい。
クラスター内のとある指標の値が、可能な限り一定になるようにしたい場合
これは例えば、各点(ここでは避難所)が「収容人数」のようなステータスを持っていて、各クラスターに分割されたとき、その値の和が一定となるようにクラスターサイズを調整したい場合である。
最終的に分割したいクラスターの数を \(N\) とした場合、以下のようなアルゴリズムが考えられる。
- \(N\)よりも小さな数 \(M\) を決める
- \(K=M\) として、K-meansクラスタリングを行う
- 各クラスターにおける値の和を求め、その比率にしたがって、各クラスターで \(N\) を分配する
- \(k\) 番目のクラスターに割り当てられた数を \(N_k\) とする
- \(N_k\) に対して 1. から同じ操作を行う
以上を \(N_k\) が分割できなくなるまで繰り返す。すなわち、少しずつ、得られたクラスターの規模に応じてクラスター数を調節しつつ、クラスタリングを行っていこうということである。

Comments