概要
フーリエ級数の定義や応用を示し、実際の計算方法を解説する。
この記事を読むことで、フーリエ級数の意味を理解し、実際に級数の値を求めることができるようになる。
また、Python言語を用いて例を可視化するコードも書く。
(2023/08/17追記:フーリエ余弦・正弦級数、複素形フーリエ級数についても網羅した)
フーリエ級数の意味と活用例
フーリエ級数は、複雑な周期関数や周期信号を単純なサイン波とコサイン波の和として表す手法である。
当初は金属板の熱伝導の研究において導入されたが、現在では電気工学や量子力学など、周期的な量を扱う分野において広く利用されている。
ようは複雑で正体不明な周期関数を、単純なサイン波とコサイン波に分解し、分解した単純な波の解を求めることで、もともとの関数の性質を見ようという考え方である。
そして、この波の重ね合わせのことをフーリエ級数という。
計算のための前提
以下の関係式が成り立つことを確認しておくと、後のフーリエ係数の計算が楽になる。
閉区間 \([-a,a]\) で関数 \(f(x)\) が、
- 偶関数ならば、 \(\int_{-a}^a f(x)dx=2\int_0^a f(x)dx\)
- 奇関数ならば、 \(\int_{-a}^a f(x)dx=0\)
また、 \([-\pi,\pi]\) で \(m,n\) を自然数とすると、
- \(\int_{-\pi}^\pi \cos nx\,dx=0\)
- \(\int_{-\pi}^\pi \sin nx\,dx=0\)
- \(\int_{-\pi}^\pi \cos mx \cos nx\,dx=\begin{cases}\pi\,(m=n) \\ 0\,(m\neq n)\end{cases}\)
- \(\int_{-\pi}^\pi \sin mx \sin nx\,dx=\begin{cases}\pi\,(m\neq n)\\ 0\,(m=n)\end{cases}\)
- \(\int_{-\pi}^\pi \cos mx \sin nx\,dx=0\)
となる。
フーリエ級数の導出
三角級数
周期 \(2\pi\) を持つ関数 \(f(x)\) が三角関数によって
$$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos nx+b_n\sin nx)$$
$$=\frac{a_0}{2}+a_1\cos x+a_2\cos 2x+\cdots+a_n\cos nx+\cdots$$
$$+b_1\sin x+b_2\sin 2x+\cdots+b_n\sin nx+\cdots \tag{1}$$
の形で表されたとする。この式を三角級数という。
未知係数の決定
次に、三角級数の式に以下の操作を行う。
- 両辺に \(1\) をかけて項別積分
- \(\int_{-\pi}^\pi f(x)dx=\frac{a_0}{2}\int_{-\pi}^\pi dx=\pi a_0\) (前提:1., 2.)
- 両辺に \(\cos mx\) をかけて項別積分
- \(\int_{-\pi}^\pi f(x)\cos mx\,dx=a_m\int_{-\pi}^\pi \cos mx\cos mx\,dx=\pi a_m\) (前提:3., 5.)
- 両辺に \(\sin mx\) をかけて項別積分
- \(\int_{-\pi}^\pi f(x)\sin mx\,dx=b_m\int_{-\pi}^\pi \sin mx\sin mx\,dx=\pi b_m\) (前提:4., 5.)
するとこの結果から、係数 \(a_0,a_1,a_2,\cdots,b_1,b_2,\cdots\) の値が決定する。
フーリエ級数の定義(どうしても条件付きになる)
しかし、上記の計算で行った項別積分はあくまで形式的なものであるため、このようにして求められた係数を持つ \((1)\) 式の三角級数が収束するとは限らない。
また収束するとしても、もとの関数 \(f(x)\) に一致するとは限らない。
そのため、関数 \(f(x)\) の三角関数による表現を等号 \(=\) を用いて表すのではなく、 \(\sim\) を用いて表すことにする(両辺が等しくなるとは限らないため)。
したがって、以上の内容をまとめると次のようになる。
周期 \(2\pi\) を持つ関数 \(f(x)\) について、
$$f(x)\sim\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx) \tag{2}$$
と表すことができ、右辺の係数は以下の式で与えられる。
$$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\,dx\,(n=0,1,2,\cdots) \tag{3}$$
$$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\,dx\,(n=1,2,\cdots) \tag{4}$$
\((2)\) 式の右辺の三角級数を、関数 \(f(x)\) のフーリエ級数またはフーリエ展開という。
また、 \((3)\) ・ \((4)\) 式によって定められる係数のことを、関数 \(f(x)\) のフーリエ係数といい、特に、 \(a_n\) のことをフーリエ余弦係数、 \(b_n\) のことをフーリエ正弦係数という。
なお、定数項を \(\frac{a_0}{2}\) としたのは、定数項をフーリエ余弦係数の一員として \((3)\) 式により一括して表すためである。
フーリエ級数の部分和
フーリエ級数の \(a_n\) と \(b_n\) を持つ項までの和を \(S_n\) として表し、その一部のみを取り出すこととする。すなわち
$$S_n=\frac{a_0}{2}+a_1\cos x+a_2\cos 2x+\cdots+a_n\cos nx$$
$$+b_1\sin x+b_2\sin 2x+\cdots+b_n\sin nx$$
であり、この \(S_n\) のことをフーリエ級数の第 \(n\) 部分和という。
フーリエ級数の例とPythonによる可視化
周期 \(2\pi\) を持ち、区間 \((-\pi,\pi]\) で定義される関数
$$f(x)=\begin{cases}0\,(-\pi< x< 0)\\1\,(0\leq x\leq\pi)\end{cases}$$
について考える。この関数のフーリエ係数は
$$a_0=\frac{1}{\pi}\int_0^{\pi}dx=1$$
$$a_n=\frac{1}{\pi}\int_0^{\pi}\cos nx\,dx=\frac{1}{\pi n}[\sin nx]_0^{\pi}=0$$
$$b_n=\frac{1}{\pi}\int_0^{\pi}\sin nx\,dx=\frac{1}{\pi n}[-\cos nx]_0^{\pi}$$
$$=\frac{1}{\pi n}\{-(-1)^n+1\}=\begin{cases}0\quad(nが偶数)\\ \frac{2}{\pi n}\quad(nが奇数)\end{cases}$$
となる。なお、 \(a_0\) は分母が0となることを避けるため別に計算した。
以上の結果から、
$$f(x)\sim\frac{1}{2}+\frac{2}{\pi}(\sin x+\frac{1}{3}\sin 3x+\frac{1}{5}\sin 5x+\cdots)$$
$$=\frac{1}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1}{2n-1}\sin(2n-1)x$$
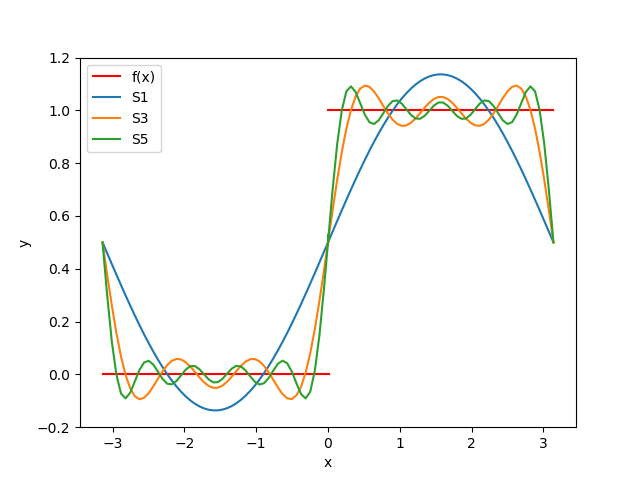
となり、 \(f(x),S_1,S_3,S_5\) を図示すると以下のようになる。
from matplotlib import pyplot as plt
import math
import numpy as np
x0 = np.linspace(-math.pi, 0.01, 50)
x1 = np.linspace(0,math.pi, 50)
x = np.hstack((x0, x1))
fx0 = np.zeros(50)
fx1 = np.ones(50)
def part_sum(X, N):
return np.array([1/2 + np.sum([math.sin((2*n+1)*x)/(2*n+1) for n in range(N)])*2/math.pi for x in X])
s1 = part_sum(x, 1)
s3 = part_sum(x, 3)
s5 = part_sum(x, 5)
plt.plot(x0, fx0, c="r", label="f(x)")
plt.plot(x1, fx1, c="r")
plt.plot(x, s1, label="S1")
plt.plot(x, s3, label="S3")
plt.plot(x, s5, label="S5")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()図によると、 \(f(x)\) が連続な点では \(n\) が大きくなるにつれて \(S_n\) が \(f(x)\) に近づいており、不連続点 \(x~0\) においては \(S_n\) が \(f(x_0-0)\) と \(f(x_0+0)\) の中点を通っている。
以上は定理として次のようにまとめられる。
周期 \(2\pi\) の関数 \(f(x)\) が区分的に滑らかならば、 \(f(x)\)のフーリエ級数は
- \(f(x)\) が連続な点 \(x\) では \(f(x)\) に収束する。
- \(f(x)\) が不連続な点 \(x\) では
$$\frac{1}{2}{f(x-0)+f(x+0)}$$
に収束する。
また、不連続点 \(x=0\) の付近では \(S_n\) がもとの関数 \(f(x)\) の値を通り越して大きく(小さく)なっているが、この「飛び出し」は \(n\) が大きくなっても無くならず、ある有限極限値に近づく。
この現象をギブス現象という。
【ギブス現象】
区分的連続微分可能な周期関数のフーリエ級数において、その関数が第1種不連続となる点(ギャップを持つ不連続点)付近では、フーリエ級数の \(n\) 次部分和が大きく振動して、部分和の最大値が関数自体の最大値より大きくなる現象
フーリエ余弦級数・フーリエ正弦級数
偶関数・奇関数のフーリエ係数
\(f(x)\) が偶関数、または奇関数のときのフーリエ係数について考える。
- \(f(x)\) が偶関数のとき
- \(f(x)\cos x\) は偶関数、 \(f(x)\sin x\) は奇関数より、
- $$a_n=\frac{2}{\pi}\int_0^{\pi}f(x)\cos nx\,dx \tag{5}$$
- $$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\,dx=0$$
- \(f(x)\) が奇関数のとき
- \(f(x)\cos x\) は奇関数、 \(f(x)\sin x\) は偶関数より、
- $$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\,dx=0$$
- $$b_n=\frac{2}{\pi}\int_{0}^{\pi}f(x)\sin nx\,dx \tag{6}$$
以上より、次のことが言える。
周期 \(2\pi\) を持つ関数 \(f(x)\) について、 \(f(x)\) が、
- 偶関数ならば、 \((5)\) 式で与えられる \(a_n\) を係数として
$$f(x)\sim\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos nx \tag{7}$$- 奇関数ならば、 \((6)\) 式で与えられる \(b_n\) を係数として
$$f(x)\sim\sum_{n=1}^{\infty}b_n\sin nx \tag{8}$$
と表される。
フーリエ余弦級数(フーリエ余弦展開)
関数 \(f(x)\) が区間 \((-\pi,\pi]\) で定義されているとき、任意の整数 \(k\) に対して
$$f(x+2kx)=f(x)\quad(-\pi< x\leq\pi)$$
と定義すると、 \(f(x)\) は全区間で定義され、周期 \(2\pi\) を持つ関数となる。
また、関数 \(f(x)\) が区間 \([0,\pi]\) で定義されているときには、
$$f(-x)=f(x)$$
と定義することによって、定義域を \((-\pi,\pi]\) に拡張すると、 \(f(x)\) は偶関数になる。
そのフーリエ級数は \((7)\) 式で与えられ、このとき \((7)\) 式を関数 \(f(x)\) の \([0,\pi]\) におけるフーリエ余弦級数またはフーリエ余弦展開という。
フーリエ正弦級数(フーリエ正弦展開)
同様に、
$$f(-x)=-f(x)$$
と定義して、定義域を \((-\pi,\pi]\) に拡張した場合、 \(f(x)\) は奇関数になる。
そのフーリエ級数は \((8)\) 式で与えられ、このとき \((8)\) 式を関数 \(f(x)\) の \([0,\pi]\) におけるフーリエ正弦級数またはフーリエ正弦展開という。
複素形フーリエ級数
三角関数を用いて表されるフーリエ級数を、オイラーの公式により変換することを考える。
オイラーの公式
$$e^{ix}=\cos x+i\sin x$$
$$e^{-ix}=\cos x-i\sin x$$
より、
$$\cos x=\frac{1}{2}(e^{ix}+e^{-ix})$$
$$\sin x=\frac{1}{2}(e^{ix}-e^{-ix})$$
が導かれ、これを用いると
$$a_n\cos nx+b_n\sin nx=a_n\frac{e^{inx}+e^{-inx}}{2}-ib_n\frac{e^{inx}-e^{-inx}}{2}$$
$$=\frac{a_n-ib_n}{2}e^{inx}+\frac{a_n+ib_n}{2}e^{-inx}$$
となる。ここで、
$$c_0=\frac{a_0}{2},\quad c_n=\frac{a_n-ib_n}{2},\quad c_{-n}=\frac{a_n+ib_n}{2}\quad(n=1,2,\cdots)$$
とおくと、フーリエ級数は
$$f(x)\sim\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx)$$
$$=c_0+\sum_{n=1}^{\infty}(c_n e^{inx}+c_{-n} e^{-inx})$$
$$=\cdots+c_{-n} e^{-inx}+\cdots+c_{-1} e^{-ix}+c_0 e^0+c_{1} e^{ix}+\cdots+c_n e^{inx}+\cdots$$
$$=\sum_{n=-\infty}^{\infty}c_n e^{inx}$$
と表される。このときのフーリエ係数は \((3),(4)\) 式より、
$$c_n=\frac{a_n-ibn}{2}$$
$$=\frac{1}{2}\left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\quad dx+\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\quad dx\right\}$$
$$=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)(\cos nx-i\sin nx)dx$$
$$=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx$$
で表される。
\(c_n\) と \(c_{-n}\) は共役であるから、上式は \(n\) が負のときも成り立つ。したがって、
周期 \(2\pi\) を持つ関数 \(f(x)\) は次の形に表される。
$$f(x)\sim\sum_{n=-\infty}^{\infty}c_n e^{inx} \tag{9}$$
$$c_n=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx\quad (n=0,\pm 1,\pm 2,\cdots) \tag{10}$$
このとき、 \((9)\) 式の右辺を関数 \(f(x)\) の複素形フーリエ級数、その係数 \((10)\) を複素形フーリエ係数という。
これと対応して、 \((2)\) 式のフーリエ級数を実数形という。


Comments