生体・生態系・経済など、「多数の要素から構成され、要素間相互作用によって、予測不能な高次の秩序や機能を生み出しうるシステム」のことを複雑システムという。
本稿では、複雑システムがもつ臨界減速(Critical Slowing Down:CSD)という性質について、数理モデルを用いて実験しながら解説する。
システムの安定は転換点で崩壊する
複雑システムは通常、安定状態を持ち、外圧の影響により微小な状態変化が生じた際には、修復力が働いて即座にもとの安定状態へと復帰する。
しかし、時に複雑システムはもとの安定状態に戻るのではなく、異なる安定状態へと遷移することがある。
このような変化が生じる臨界閾値は「転換点」と呼ばれ、その前後でシステムに大きな変動が見られることが確認されている。
転換点付近で臨界減速が生じる
システムの数理モデルによる実験
微分方程式
$$\frac{dx}{dt}=-p+3x-x^{3}+\epsilon$$
で表現されるシステム \(x\) の時間変動を考える。
この \(x\) は時間 \(t\) とともにパラメータ \(p\) が変化することで、転換点を迎えることが知られている。
なお、\(\epsilon\) は平均 \(0\) , 標準偏差 \(\sigma\) の正規分布にしたがうノイズであり、外圧による微小変化を表現している。
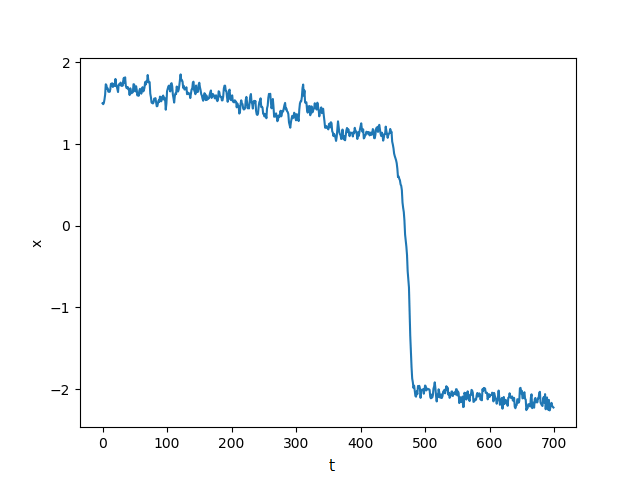
転換点付近では、外圧による微小変化から安定状態への復帰に遅れが生じる。
この現象のことを臨界減速という。
臨界減速を予測する指標
臨界減速は、 \(x\) の標準偏差と自己相関係数の上昇として捉えることができる。
上図において、 \(t\) が \(100~200\) (転換点から遠い)と \(300~400\) (転換点に近い)の範囲にあるときの標準偏差と自己相関係数について分析する。
肉眼的にはあまり違いがないように見えるが、図示してみると差は一目瞭然である。
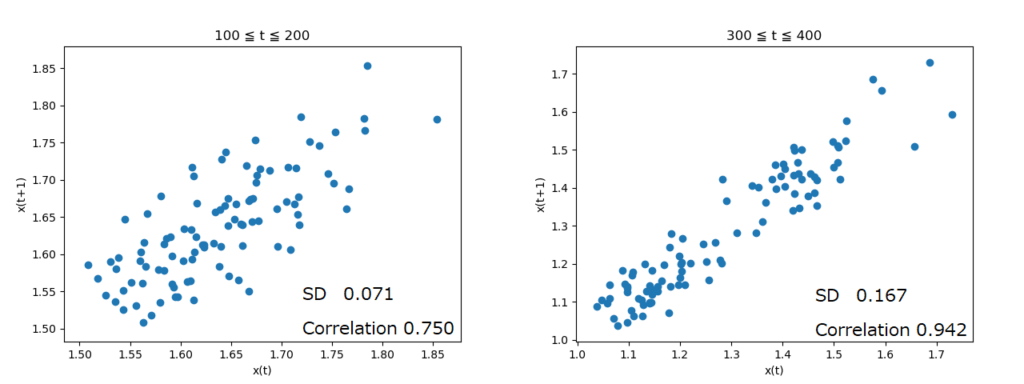
この図は、時間 \(t\) における \(x\) の値を横軸、時間 \(t+1\) における \(x\) の値を縦軸にとり、各点をプロットしたものである。
転換点付近の方がより直線に近い分布を示し、自己相関係数(Correlation)も \(0.750から0.942\) まで上昇している。
また、標準偏差(SD)も \(0.071\) から \(0.167\) と大きな上昇が見られている。
以上の結果は、感覚的には、システムが転換点に近づくにつれ、外圧に対する脆弱性が増していると考えることができる(転換点の存在、転換点付近での標準偏差と自己相関係数の上昇についての数学的な説明は、Scheffer et al. 2009 : Box 1~3参照)。
参考文献
- Scheffer, Marten, Jordi Bascompte, William A. Brock, Victor Brovkin, Stephen R. Carpenter, Vasilis Dakos, Hermann Held, Egbert H. van Nes, Max Rietkerk, and George Sugihara. 2009. “Early-warning signals for critical transitions,” Nature, 461(3): 53-59.

Comments