概要
この記事では、クオータニオン(四元数)を用いて3次元空間での回転を表現する方法と、その原理について解説する。
ここでの式変形は、以下の記事で述べたクオータニオンの定義や性質を前提とするので、参考にしてほしい。

複素数による回転
2次元平面上の点 \((x_1, y_1)\) に対応する複素数
$$z=x_1+y_1i$$
に、複素数
$$r=\cos{\theta}+i\sin{\theta}$$
を掛けると、点を原点周りに \(\theta\) だけ回転させた位置 \((x_2, y_2)\) に移すことができる。
要素を書き下すと
$$rz=(\cos{\theta}+i\sin{\theta})(x_1+y_1i)$$
$$=(x_1\cos{\theta}-y_1\sin{\theta})+(x_1\sin{\theta}+y_1\cos{\theta})$$
より、
$$x_2=x_1\cos{\theta}-y_1\sin{\theta},\quad y_2=x_1\sin{\theta}+y_1\cos{\theta}$$
となる。これを行列を用いて表現すると、
$$\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}=\begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}\begin{bmatrix} x_1 \\ y_1 \end{bmatrix}$$
となり、複素数 \(r\) と回転行列の関係を見ることができる。
ここで、
$$\cos^2{\theta}+\sin^2{\theta}=1$$
より、複素数 \(r\) のノルムは1である。
クオータニオンによる回転
四次元の回転
ノルムが1のクオータニオン(単位クオータニオン)も、複素数と同様、回転を表現することができる。ただし、複素数の回転が2次元の回転であるのに対し、クオータニオンによる回転は4次元となる。
2平面上の回転(左側からの掛け算)
4次元空間の点 \((w, x, y, z)\) をクオータニオンで表現すると
$$\mathbf{v}=w+xi+yj+zk$$
となり、これに複素数と類似した、2要素のみが非零の値を持つ単位クオータニオン
$$\mathbf{q}_x=\cos{\theta}+i\sin{\theta}$$
を左から掛けると
$$\mathbf{q}_x\mathbf{v}=(w\cos{\theta}-x\sin{\theta})+(w\sin{\theta}+x\cos{\theta})i$$
$$+(y\cos{\theta})j+(z\cos{\theta})k+(y\sin{\theta})ij+(z\sin{\theta})ik$$
$$=(w\cos{\theta}-x\sin{\theta})+(w\sin{\theta}+x\cos{\theta})i$$
$$+(y\cos{\theta})j+(z\cos{\theta})k+(y\sin{\theta})k-(z\sin{\theta})j$$
$$=(w\cos{\theta}-x\sin{\theta})+(w\sin{\theta}+x\cos{\theta})i$$
$$+(y\cos{\theta}-z\sin{\theta})j+(y\sin{\theta}+z\cos{\theta})k$$
となり、要素ごとに対応を見ると
$$\begin{bmatrix} w\cos{\theta}-x\sin{\theta} \\ w\sin{\theta}+x\cos{\theta} \\ y\cos{\theta}-z\sin{\theta} \\ y\sin{\theta}+z\cos{\theta} \end{bmatrix}\leftarrow\begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}$$
と表現できる。幾何学的には、点をYZとWXの2つの平面上で、同時に \(\theta\) だけ回転させる操作に相当する。
同様に、
$$\mathbf{q}_y=\cos{\phi}+j\sin{\phi}$$
を左側から掛けると
$$\begin{bmatrix} w\cos{\phi}-y\sin{\phi} \\ z\sin{\phi}+x\cos{\phi} \\ w\sin{\phi}+y\cos{\phi} \\ z\cos{\phi}-x\sin{\phi} \end{bmatrix}\leftarrow\begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}$$
となり、ZXとWYの2平面上での回転を表し、
$$\mathbf{q}_z=\cos{\psi}+k\sin{\psi}$$
を左側から掛けると
$$\begin{bmatrix} w\cos{\psi}-z\sin{\psi} \\ x\cos{\psi}-y\sin{\psi} \\ w\sin{\psi}+z\cos{\psi} \\ x\sin{\psi}+y\cos{\psi} \end{bmatrix}\leftarrow\begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}$$
となり、XYとWZの2平面上での回転を表す。
複素共役クオータニオンの回転
上記のような簡素なクオータニオンの複素共役クオータニオンを考えると、
$$\mathbf{q}_x^*=\cos{\theta}-i\sin{\theta}=\cos(-\theta)+i\sin(-\theta)$$
より、逆方向の回転を表す。
2平面上の回転(右側からの掛け算)
クオータニオンは交換則を満たさないため、単位クオータニオンを右から掛けた場合の回転についても検討する必要がある。実際に計算を行うと
$$\begin{bmatrix} w\cos{\theta}-x\sin{\theta} \\ w\sin{\theta}+x\cos{\theta} \\ y\cos{\theta}+z\sin{\theta} \\ y\sin{\theta}-z\cos{\theta} \end{bmatrix}\leftarrow\begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}$$
という変換を行うことになり、WX平面に関しては \(\theta\) 、YZ平面に関しては \(-\theta\) の回転に相当する。
同様に、 \(\mathbf{q}_y\) を右側から掛けるとWY平面に関して \(\theta\) 、ZX平面に関して \(-\theta\) の回転に相当し、 \(\mathbf{q}_z\) を右側から掛けるとWZ平面に関して \(\theta\) 、XY平面に関して \(-\theta\) の回転に相当する。
三次元の回転
1平面(1軸)上の回転
これまでの分析を踏まえると、単位クオータニオンを左右から掛けることで、任意の1平面、すなわち、三次元上の任意の1軸まわりの回転を表現することができる。
単位クオータニオン
$$\mathbf{q}_X=\cos{\frac{\theta}{2}}+i\sin{\frac{\theta}{2}}$$
を左右から掛けると
$$\mathbf{q}_X\mathbf{v}\mathbf{q}_X^*=w+xi+(y\cos{\theta}-z\sin{\theta})j+(y\sin{\theta}+z\cos{\theta})k$$
となる。これはYZ平面上で点を \(\theta\) だけ回転する操作に相当し、三次元空間におけるYZ平面上での回転はX軸まわりの回転に等しい。この結果は、以下のような2段階の変換として考えることができる。
$$\begin{bmatrix} w \\ x \\ y\cos{\theta}-z\sin{\theta} \\ y\sin{\theta}+z\cos{\theta} \end{bmatrix}\leftarrow\begin{bmatrix} w\cos{\frac{\theta}{2}}-x\sin{\frac{\theta}{2}} \\ w\sin{\frac{\theta}{2}}+x\cos{\frac{\theta}{2}} \\ y\cos{\frac{\theta}{2}}-z\sin{\frac{\theta}{2}} \\ y\sin{\frac{\theta}{2}}+z\cos{\frac{\theta}{2}} \end{bmatrix}\leftarrow\begin{bmatrix} w \\ x \\ y \\ z \end{bmatrix}$$
まず、左から掛けた \(\mathbf{q}_X\) によって、YZ・WXの2平面に関して \(\frac{\theta}{2}\) の回転を行う。その後、右から掛けた \(\mathbf{q}_X^*\) によって、YZ平面に関して \(\frac{\theta}{2}\) 、WX平面に関して \(-\frac{\theta}{2}\) の回転(右から \(\mathbf{q}_X\) を掛けた場合の逆回転)を行うことで、WX平面に関する回転が元に戻り、YZ平面に対する倍角の回転のみが残る。
クオータニオンの結合による3軸上の回転
以下、3次元空間の点 \(x, y, z\) を表現した、「ベクトル」部のみから成るクオータニオン
$$\mathbf{v}=xi+yj+zk$$
の回転を考える。
この点を、X軸周りに \(\theta\) 、次にY軸周りに \(\phi\) 、最後にZ軸周りに \(\psi\) 回転した結果は、
$$\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X\mathbf{v}\mathbf{q}_X^*\mathbf{q}_Y^*\mathbf{q}_Z^*$$
と表せる。ただし、
$$\mathbf{q}_Y=\cos{\frac{\phi}{2}}+j\sin{\frac{\phi}{2}}$$
$$\mathbf{q}_Y=\cos{\frac{\psi}{2}}+k\sin{\frac{\psi}{2}}$$
である。クオータニオンは結合則を満たすため、上の回転は
$$\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X\mathbf{v}\mathbf{q}_X^*\mathbf{q}_Y^*\mathbf{q}_Z^*=(\mathbf{q}_Z(\mathbf{q}_Y(\mathbf{q}_X\mathbf{v}\mathbf{q}_X^*)\mathbf{q}_Y^*)\mathbf{q}_Z^*)$$
の3段階の操作として捉えることができる。また、同様に結合則から
$$\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X\mathbf{v}\mathbf{q}_X^*\mathbf{q}_Y^*\mathbf{q}_Z^*=(\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X)\mathbf{v}(\mathbf{q}_X^*\mathbf{q}_Y^*\mathbf{q}_Z^*)$$
$$=(\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X)\mathbf{v}(\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X)^*$$
となることから、この回転を表すクオータニオンは
$$\mathbf{q}=\mathbf{q}_Z\mathbf{q}_Y\mathbf{q}_X$$
と書ける。 \(\mathbf{q}_X,\mathbf{q}_Y,\mathbf{q}_Z\) の順序は、回転を行う順番によって異なり、例えば、Z軸まわり→X軸まわり→Y軸まわりの回転を行った場合、
$$\mathbf{q}=\mathbf{q}_Y\mathbf{q}_X\mathbf{q}_Z$$
となる。
以上より、クオータニオンと3次元空間における回転について、次のことが言える。
クオータニオンによる回転の表現
- 3次元空間の点(ベクトル)は、クオータニオンの「ベクトル」部のみを用いて表現できる
- 3次元空間における任意の回転は、クオータニオンを用いて表現できる
- 点を表すクオータニオンを \(\mathbf{v}\) 、回転を表すクオータニオンを \(\mathbf{q}\) 、その複素共役を \(\mathbf{q}^*\) とすると、点の回転は \(\mathbf{qvq}^*\) と表せる
任意の軸に関する回転
クオータニオンによって表せる特殊な回転として、任意の回転軸を表すベクトルを \(\mathbf{\bar{n}}=(n_x, n_y, n_z)\) 、回転角を \(\theta\) とすると、クオータニオン
$$\mathbf{q}=\cos{\frac{\theta}{2}}+\mathbf{\bar{n}}\sin{\frac{\theta}{2}}$$
$$=\cos{\frac{\theta}{2}}+n_x\sin{\frac{\theta}{2}}+n_y\sin{\frac{\theta}{2}}+n_z\sin{\frac{\theta}{2}}$$
によって表される回転 \(\mathbf{qvq}^*\) は、点を軸 \(\mathbf{\bar{n}}\) まわりに \(\theta\) だけ回転する操作を意味する。
回転の行列表現
3次元空間の点と回転を、それぞれ
$$\mathbf{v}=0+\mathbf{\bar{v}}=v_1+v_2+v_3$$
$$\mathbf{q}=q_0+\mathbf{\bar{q}}=q_0+q_1+q_2+q_3$$
というクオータニオンで表現したとき、点の回転は
$$\mathbf{qvq}^*=(q_0+\mathbf{\bar{q}})(0+\mathbf{\bar{v}})(q_0-\mathbf{\bar{q}})$$
$$=q_0^2\mathbf{\bar{v}}-q_0\mathbf{\bar{v}\bar{q}}+q_0\mathbf{\bar{q}\bar{v}}-\mathbf{\bar{q}\bar{v}\bar{q}}$$
$$=q_0^2\mathbf{\bar{v}}-q_0\mathbf{\bar{v}\bar{q}}+q_0\mathbf{\bar{q}\bar{v}}-\mathbf{\bar{q}}(\mathbf{\bar{v}\bar{q}})$$
これを行列で表現すると
$$q_0^2\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}-q_0\begin{bmatrix} 0 & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & 0 & q_{3} & -q_{2} \\ q_{2} & -q_{3} & 0 & q_{1} \\ q_{3} & q_{2} & -q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}+q_0\begin{bmatrix} 0 & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & 0 & -q_{3} & q_{2} \\ q_{2} & q_{3} & 0 & -q_{1} \\ q_{3} & -q_{2} & q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}$$
$$-\begin{bmatrix} 0 & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & 0 & -q_{3} & q_{2} \\ q_{2} & q_{3} & 0 & -q_{1} \\ q_{3} & -q_{2} & q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & 0 & q_{3} & -q_{2} \\ q_{2} & -q_{3} & 0 & q_{1} \\ q_{3} & q_{2} & -q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}$$
$$=\begin{bmatrix} q_0^2 & 0 & 0 & 0 \\ 0 & q_0^2 & 0 & 0 \\ 0 & 0 & q_0^2 & 0 \\ 0 & 0 & 0 & q_0^2 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}+\begin{bmatrix} 0 & q_{0}q_{1} & q_{0}q_{2} & q_{0}q_{3} \\ -q_{0}q_{1} & 0 & -q_{0}q_{3} & q_{0}q_{2} \\ -q_{0}q_{2} & q_{0}q_{3} & 0 & -q_{0}q_{1} \\ -q_{0}q_{3} & -q_{0}q_{2} & q_{0}q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}$$
$$+\begin{bmatrix} 0 & -q_{0}q_{1} & -q_{0}q_{2} & -q_{0}q_{3} \\ q_{0}q_{1} & 0 & -q_{0}q_{3} & q_{0}q_{2} \\ q_{0}q_{2} & q_{0}q_{3} & 0 & -q_{0}q_{1} \\ q_{0}q_{3} & -q_{0}q_{2} & q_{0}q_{1} & 0 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}+\begin{bmatrix} q_{1}^2+q_{2}^2+q_{3}^2 & 0 & 0 & 0 \\ 0 & q_{1}^2-q_{2}^2-q_{3}^2 & 2q_{1}q_{2} & 2q_{1}q_{3} \\ 0 & 2q_{1}q_{2} & q_{2}^2-q_{1}^2-q_{3}^2 & 2q_{2}q_{3} \\ 0 & 2q_{1}q_{3} & 2q_{2}q_{3} & q_{3}^2-q_{1}^2-q_{2}^2 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}$$
$$=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 2(q_{0}^2+q_{1}^2)-1 & 2(q_{1}q_{2}-q_{0}q_{3}) & 2(q_{1}q_{3}+q_{0}q_{2}) \\ 0 & 2(q_{1}q_{2}+q_{0}q_{3}) & 2(q_{0}^2+q_{2}^2)-1 & 2(q_{2}q_{3}-q_{0}q_{1}) \\ 0 & 2(q_{1}q_{3}-q_{0}q_{2}) & 2(q_{2}q_{3}+q_{0}q_{1}) & 2(q_{0}^2+q_{3}^2)-1 \end{bmatrix}\begin{bmatrix} 0 \\ v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}$$
となる。式変換の途中で、 \(q_{0}^2+q_{1}^2+q_{2}^2+q_{3}^2=1\) の関係式を用いた。
1行・1列を無視すると、3次元空間の点 \(\mathbf{\bar{v}}\) の回転は
$$\begin{bmatrix} 2(q_{0}^2+q_{1}^2)-1 & 2(q_{1}q_{2}-q_{0}q_{3}) & 2(q_{1}q_{3}+q_{0}q_{2}) \\ 2(q_{1}q_{2}+q_{0}q_{3}) & 2(q_{0}^2+q_{2}^2)-1 & 2(q_{2}q_{3}-q_{0}q_{1}) \\ 2(q_{1}q_{3}-q_{0}q_{2}) & 2(q_{2}q_{3}+q_{0}q_{1}) & 2(q_{0}^2+q_{3}^2)-1 \end{bmatrix}\begin{bmatrix} v_{1} \\ v_{2} \\ v_{3} \end{bmatrix}=\mathbf{Q\bar{v}}$$
という回転行列 \(\mathbf{Q}\) を用いて表現できる。
点の回転と座標の回転
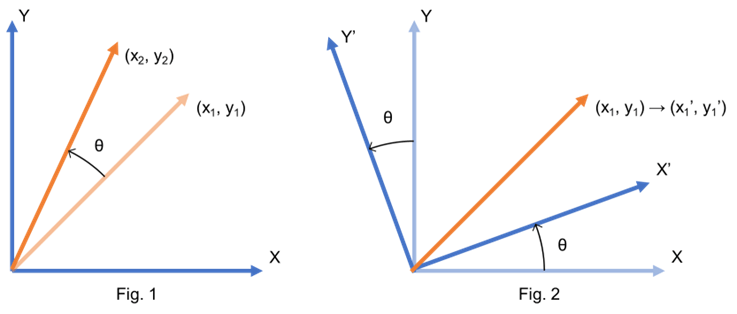
「3次元空間での回転」には、Fig.1のように座標系を固定して点を回転する場合と、Fig.2のように点を固定して座標系を回転する場合の2種類がある。後者の場合、座標の取り方が変わるので、 \((x_1, y_1)\) の点は \(x_1', y_1'\) に表現が変わる。
上述のとおり、点 \(\mathbf{v}=0+\mathbf{\bar{v}}\) の回転は、回転クオータニオン \(\mathbf{q}\) または回転行列 \(\mathbf{Q}\) を用いて
$$\mathbf{qvq}^*$$
$$\mathbf{Q\bar{v}}$$
と表せる。
対して座標系を \(\theta\) 回転する操作は、点を固定された座標系に対して \(-\theta\) 回転する操作に等しい。よって、同じ回転クオータニオンや回転行列を用いて
$$\mathbf{q}^*\mathbf{vq}$$
$$\mathbf{Q}^{-1}\mathbf{\bar{v}}=\mathbf{Q}^\top\mathbf{\bar{v}}$$
と表せる。下式の等号において、 \(\mathbf{Q}\) が直交行列であることを用いた。


Comments