一様分布の最尤推定

確率・統計

2021.09.302023.07.22

公式

一様分布 $U(x|a,b)$ のパラメータについて、データ $X=\{x_1,x_2,\ldots,x_N\}$ を用いて最尤推定を行ったとき

$$a=\min(X), b=\max(X)$$

となる。ここで、 $\min(A), \max(A)$ はそれぞれ、集合 $A$ の最小値と最大値を表す。

導出

一様分布の定義・性質については

一様分布の定義・性質とその証明

定義連続変数 $x$ が、有限区間 $x\in$ で一様分布する場合、その確率密度関数 $p(x)$ は $$p(x)=\frac{1}{b-a}$$ で定義される。より一般に、分布が一様分布であることを明示して $$p(x...

を参照のこと。

$$p(x)=U(x|a,b)=\begin{cases}\frac{1}{b-a}&(a\leq x\leq b)\\0&(else)\end{cases}$$

より、データ $X$ に対する尤度を $\mathcal{L}(X)$ とおくと、

$$\mathcal{L}(X)=\prod_{i}p(x_i)$$

より

$$\mathcal{L}(X)=\begin{cases}\frac{1}{(b-a)^N}&(\forall x_i, a\leq x_i\leq b)\\0&(else)\end{cases}$$

となる。すなわち、この尤度を最大化するためには、 $b-a$ の値を小さくする必要があるが、同時にすべての $x_i$ が $a\leq x_i\leq b$ の範囲に入るようにしなければならない。

よって、必要最小限の範囲を考えると

$$a=\min(X), b=\max(X)$$

が導かれる。

つまり、データが一様分布の範囲外にあることは最尤推定からして「あり得ない」が、かといって範囲を広げすぎても尤もらしさが減るのである。

例

実験と結果

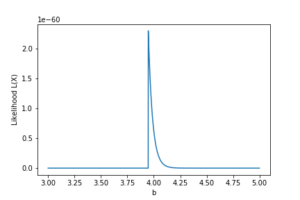
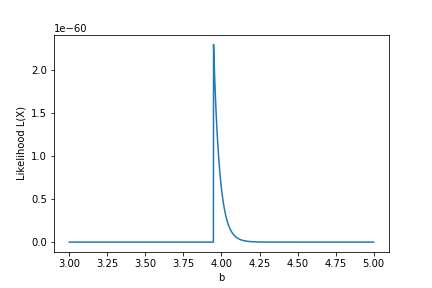
$[0, 4]$ の範囲で発生させた乱数に関し、 $U(x|0,b)$ のパラメータ $b$ についての最尤推定を行うと、 $b\simeq 3.95$ となった。

参考図

$b$ の値を変化させたときの、尤度の変化。

実験に用いたコード

import numpy as np
from matplotlib import pyplot as plt

def uniform(x, b):
    ans = np.zeros_like(x)
    ans[(x >= 0) & (x <= b)] = 1 / b
    return ans

b_arr = np.arange(2000) * 0.001 + 3
plt.plot(b_arr, [uniform(x, b).prod() for b in b_arr])
plt.ylabel("Likelihood L(X)")
plt.xlabel("b")
plt.savefig("uniform_mle.png")
plt.show()

注意

ここまで見てきたとおり、一様分布の最尤推定には最小値・最大値を用いる。

そのため、一様分布の最尤推定は外れ値を持つデータに対して非常に脆弱である。これは、一様分布がデータ範囲に厳格な境界を持っていることに由来する。

したがって、一様分布の最尤推定を行う際には何らかの方法で外れ値を除外する必要がある。

また、最小値と最大値を（それがどんなに離れているにも関わらず）重視することは、一様分布的には「尤もらしい」のだが、そもそも一様分布に当てはめること自体が「尤もらしくない」場合もあることを考慮すべきだろう。

公式

導出

例

実験と結果

参考図

実験に用いたコード

注意

Comments