以前

にて、
EMアルゴリズムを適用するに際し、一様分布のような明確な境界を持つ分布を使用すると、少し特殊な配慮が必要になる
と述べた。
本記事では、実践を通して、こうした有界な分布を用いたEMアルゴリズムがどのように失敗するかを体験し、その解決法について探る。
実験
参考記事
本記事で行う実験は、先述した

で扱われているものとほぼ同様である。
当該記事ですでに解説した内容については省略するので、適宜参照してほしい。
データ \(\mathbf{X}\)
一様分布 \(U(x|0, 0.5)\) から発生させたデータ点200個と、指数分布 \(\mathrm{Ex}(x|\frac{1}{2})=\frac{1}{2}\exp\left(-\frac{x}{2}\right)\) から発生させたデータ点800個を結合した、計 \(N=1000\) 個をデータ \(\mathbf{X}\) とする。
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(42)
# exponentialのscaleはλの逆数であることに注意
x = np.hstack((np.random.random(size=200) * 0.5, np.random.exponential(size=800, scale=2)))
plt.hist(x, bins=200)
plt.ylabel("number")
plt.xlabel("value")
plt.title("Histogram of X")
plt.tight_layout()
plt.savefig("hist_x.png")
plt.show()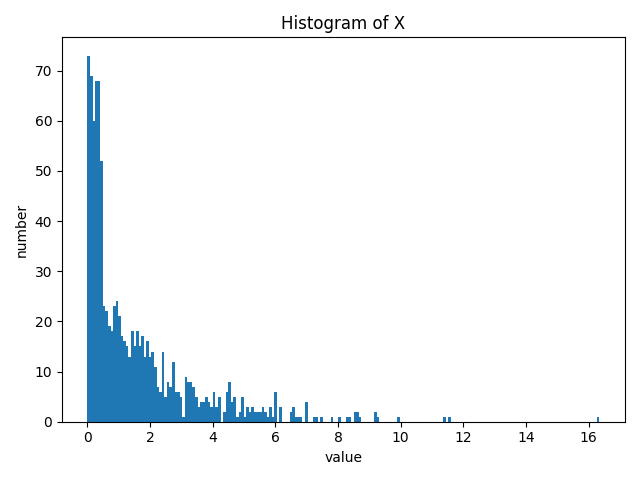
混合分布
上記のデータを用いて、2種類の分布からなる以下の混合分布について最尤推定する。
$$p(x|\rho, \alpha, \lambda)=\rho\frac{1}{\alpha}\mathbb{I}[0\leq x\leq\alpha]+(1-\rho)\lambda\exp(-\lambda x)\tag{11}$$
ただし
$$\mathbb{I}[0\leq x\leq\alpha]=\begin{cases}1&(0\leq x\leq\alpha)\\0&(\text{else})\end{cases}$$
を意味し、すなわち第1項が一様分布 \(U(x|0,\alpha)\) 、第2項が指数分布 \(\mathrm{Ex}(x|\lambda)\) である。
def p1(x, alpha):
ans = np.zeros_like(x)
ans[(0 <= x) & (x <= alpha)] = 1/alpha
return ans
def p2(x, lamb):
return lamb * np.exp(-lamb * x)
def likelihood(x, rho, alpha, lamb):
return rho * p1(x, alpha) + (1 - rho) * p2(x, lamb)Eステップ
潜在変数 \(\mathbf{Z}=\{z_{nk}\}\) の期待値は次のようになる。
$$\mathbb{E}[z_{n1}]=\frac{\rho^{\text{old}}\frac{1}{\alpha^{\text{old}}}\mathbb{I}[0\leq x_n\leq\alpha]}{\rho^{\text{old}}\frac{1}{\alpha^{\text{old}}}\mathbb{I}[0\leq x_n\leq\alpha]+(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}$$
$$\mathbb{E}[z_{n2}]=\frac{(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}{\rho^{\text{old}}\frac{1}{\alpha^{\text{old}}}\mathbb{I}[0\leq x_n\leq\alpha]+(1-\rho^{\text{old}})\lambda^{\text{old}}\exp(-\lambda^{\text{old}}x)}$$
def e_step(x, rho, alpha, lamb):
e1 = rho * p1(x, alpha) / likelihood(x, rho, alpha, lamb)
return e1, 1 - e1Mステップ
最大化すべき関数は
$$\mathcal{Q}(\rho, \alpha, \lambda, \rho^{\text{old}}, \alpha^{\text{old}}, \lambda^{\text{old}})=\sum_{n=1}^{N}\left[\mathbb{E}[z_{n1}]\left(\ln\rho-\ln\alpha+\ln\mathbb{I}[0\leq x_n\leq\alpha]\right)+\mathbb{E}[z_{n2}]\left\{\ln(1-\rho)+\ln\lambda-\lambda x_n\right\}\right]$$
である。
\(\rho^{\text{new}},\lambda^{\text{new}}\) は以下のように求められる。
$$\rho^{\text{new}}=\frac{1}{N}\sum_{n=1}^{N}\mathbb{E}[z_{n1}]$$
$$\lambda^{\text{new}}=\frac{\sum_{n=1}^{N}\mathbb{E}[z_{n2}]}{\sum_{n=1}^{N}\mathbb{E}[z_{n2}]x_n}$$
次に、 \(\alpha^{\text{new}}\) を求める。
以下の議論は、一様分布の最尤推定の記事が参考になる。
\(\alpha\) に関係する項について抜き出すと
$$\sum_{n=1}^{N}\mathbb{E}[z_{n1}]\left(-\ln\alpha+\ln\mathbb{I}[0\leq x_n\leq\alpha]\right)$$
であるが、 \(\mathbb{E}[z_{n1}]=0\) となる \(n\) については、これらの項の影響は \(0\) であるので無視して良い。
\(\mathbb{E}[z_{n1}]>0\) となる \(n\) については、 \(\mathbb{I}[0\leq x_n\leq\alpha]=0\) となった時点で対数尤度全体が \(-\infty\) となってしまうので、すべての \(x_n\) がこの範囲内に入るよう \(\alpha\) を十分大きく設定しなければならない。
また、 \(-\ln\alpha\) を大きくするためには、 \(\alpha\) は可能な限り小さくする必要がある。
以上2つの条件を総合すると
$$\alpha^{\text{new}}=\max\{x_n|\forall n,\mathbb{E}[z_{n1}]>0\}$$
となる。
def m_step(x, e1, e2):
r_tmp = e1.mean()
a_tmp = x[e1 > 0].max()
l_tmp = e2.sum()/(e2*x).sum()
return r_tmp, a_tmp, l_tmp結果
パラメータの初期値を \(\rho=0.5,\alpha=1.0,\lambda=1.0\) として、Eステップ/Mステップによる更新を100回程度行った。
rho = 0.5
alpha = 1.0
lamb = 1.0
like = []
for i in range(101):
if i % 10 == 0:
print("iter={:>3} | rho={:.3f}, alpha={:.3f}, lamb={:.3f}".format(i, rho, alpha, lamb))
e1, e2 = e_step(x, rho, alpha, lamb)
rho, alpha, lamb = m_step(x, e1, e2)
like.append(np.log(likelihood(x, rho, alpha, lamb)).sum())
見てわかる通り、 \(\alpha\) の値がほとんど更新されておらず、 \(\rho\) も非常に小さい。
正常な推定ができているとは言い難い結果であるが、なぜこのような失敗が生じたのだろうか?
考察
失敗の原因
結論から言うと、失敗の原因は、このアルゴリズムでは \(\alpha\) の値が更新され得ないことにある。
一度データ中の任意の点 \(x_k\) が範囲 \(0\leq x_k\leq\alpha\) の中に組み込まれると、Eステップ/Mステップを何度繰り返しても、この値に対する一様分布の負担率が \(0\) となることはない。
よって、この値を範囲外に置くような \(\alpha\) の縮小は許容されず、一様分布の形状は現実離れしたものに留まる。
そのため、この現実離れした一様分布はほぼ無視して、柔軟な指数分布でのみフィッティングを行おうとした結果、 \(\rho\) の値が非常に小さくなったのである。
解決策
一様分布の最尤推定

でも述べた通り、一様分布のパラメータを求めるためにはデータの最大値を使う。
なぜならば、データは少なくとも一様分布の範囲内に収まっていなければならないためである。
しかし、これは一様分布単体で最尤推定を行う場合の話である。
今回は混合分布であるため、一様分布の範囲外にデータ点が存在しても、それは他の分布から生じたものだとみなすことができる。
したがって、負担率(潜在変数の期待値)をより柔軟に考えてみたい。
すなわち、負担率によって \(\alpha\) の更新が制限されるのを避け、様々な \(\alpha\) の値を試すことを考える。
ここで、理想的にはすべてのデータ点について \(\alpha=x_k\) と置いて試してみるのが良いが、その場合計算量が膨大になるため、各イテレーションで数十個のデータ点をサンプルすることにする。
また逆に、「負担率によって \(\alpha\) の更新が制限される」のを避けた場合、今度は「サンプルした \(\alpha\) によって負担率が制限される」ことになる。
具体的には、 \(x_n\) が一様分布の範囲外に存在する場合、
$$\mathbb{E}[z_{n1}]=0$$
となる。
したがって、各イテレーションの前に \(\alpha\) をサンプリングするステップを置き、それらの値に基づいてEステップ/Mステップを実行する。
その結果、尤度が最大となるパラメータの組のみを保存し、次のイテレーションへと進めば良い。
再実験
上記のアルゴリズムは以下のように実装される。
rho = 0.5
alpha = 1.0
lamb = 1.0
like = []
for i in range(101):
if i % 10 == 0:
print("iter={:>3} | rho={:.3f}, alpha={:.3f}, lamb={:.3f}".format(i, rho, alpha, lamb))
# 50個のデータ点をalphaの候補としてサンプリング
# ただし、現在のalphaの値も追加する
alpha_cand = np.hstack(([alpha], np.random.choice(x, 50)))
# パラメータ保存用の変数
r_save, a_save, l_save = rho, alpha, lamb
loglike_save = -np.inf
# 各alphaの候補についてEステップ/Mステップを行う
for a in alpha_cand:
e1, e2 = e_step(x, rho, a, lamb)
r_tmp, a_tmp, l_tmp = m_step(x, e1, e2)
loglike_tmp = np.log(likelihood(x, r_tmp, a_tmp, l_tmp)).sum()
# 対数尤度が最大となるパラメータの組を保存
if loglike_tmp > loglike_save:
r_save, a_save, l_save = r_tmp, a_tmp, l_tmp
loglike_save = loglike_tmp
rho, alpha, lamb = r_save, a_save, l_save
like.append(loglike_save)
今度は正常に推定が行われていることが見て取れる。
また、ヒストグラムと分布を重ねても、推定の妥当性を見ることができる。
_, b, _ = plt.hist(x, bins=200, density=True, label="X")
uni = p1(b, alpha)*rho
exp = p2(b, lamb)*(1-rho)
plt.plot(b, uni, label=r"$\frac{1}{\alpha}$")
plt.plot(b, exp, label=r"$\lambda\exp(-\lambda x)$")
plt.plot(b, uni + exp, linestyle="--", label="Sum")
plt.legend()
plt.ylabel("pdf")
plt.xlabel("value")
plt.ylim(0, 1)
plt.tight_layout()
plt.savefig("hist_and_dist_uni.png")
plt.show()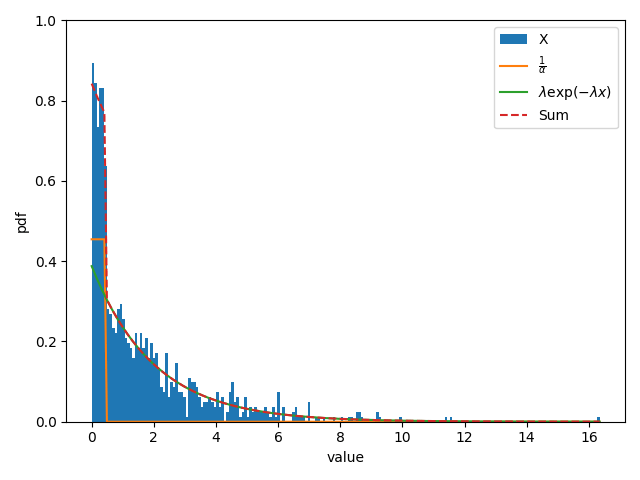
まとめ
今回の問題点は、「境界を持つ」という一様分布の性質に起因する。
例えばガウス分布には範囲というものが存在せず、いかに平均から乖離した値であっても、その値が生じる確率は \(0\) ではない。
しかし、一様分布には値の範囲があって、その外部にある値が生じることは「絶対に」ない。
本記事の内容は、このように推定の途中段階で「絶対に」と言い切ってしまうと、あまり良い結果をもたらさない、ということの教訓なのかもしれない。

Comments