定義
連続変数 \(x\) が、有限区間 \(x\in[a,b]\) で一様分布する場合、その確率密度関数 \(p(x)\) は
$$p(x)=\frac{1}{b-a}$$
で定義される。
より一般に、分布が一様分布であることを明示して
$$p(x)=U(x|a,b)=\frac{1}{b-a}$$
とも書かれる。
性質
公式
平均
$$\mathbb{E}[x]=\frac{(b+a)}{2}$$
分散
$$\mathrm{var}[x]=\frac{(b-a)^{2}}{12}$$
エントロピー
$$\mathrm{H}[x]=\ln{(b-a)}$$
公式の証明
平均
$$\mathbb{E}[x]=\int_{a}^{b}\frac{x}{b-a}dx=\frac{1}{b-a}\left[\frac{1}{x^{2}}\right]_{a}^{b}$$
$$=\frac{b^{2}-a^{2}}{2(b-a)}=\frac{(b+a)}{2}$$
分散
$$\mathrm{var}[x]=\mathbb{E}[x^{2}]-(\mathbb{E}[x])^{2}=\int_{a}^{b}\frac{x^{2}}{b-a}dx-\left(\frac{(b+a)}{2}\right)^{2}$$
$$=\frac{b^{3}-a^{3}}{3(b-a)}-\frac{(b+a)^{2}}{4}=\frac{b^{2}+ba+a^{2}}{3}-\frac{(b+a)^{2}}{4}=\frac{(b-a)^{2}}{12}$$
エントロピー
$$\mathrm{H}[x]=-\int_{a}^{b}\frac{1}{b-a}\ln{\frac{1}{b-a}}dx=\frac{1}{b-a}\ln{(b-a)}\int_{a}^{b}dx$$
$$=\left\{\frac{1}{b-a}\ln{(b-a)}\right\}(b-a)=\ln{(b-a)}$$
内分点に関する定理
変数 \(x\) の分布が \(U(x|0,1)\) であるとき、変数 \(y=a+(b-a)x\) の分布は
$$U(y|a,b)$$
となる。
内分点に関する定理の解説
上記の定理は、区間 \(y\in[a,b]\) を内分する点 \(y\) に関する性質を表している。
\(y=a+(b-a)x=(1-x)a+bx\) を図示すると、以下のような関係になる。
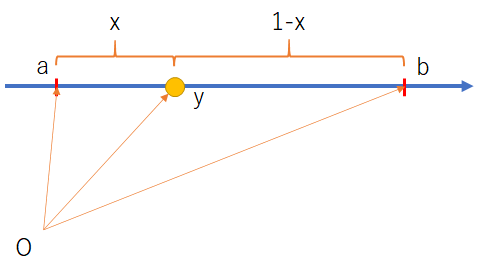
(上図では、内分をベクトル的にとらえやすくするため、本来数直線上にある原点を外部に置いた。内分点のベクトル表現については、各種高校数学の教科書を参照)
したがって、区間 \(y\in[a,b]\) を内分する点 \(y\) の一様分布を考える問題は、点 \(a\) からの距離の割合 \(x\) を \(x\in[0,1]\) の範囲で一様分布させることに帰着できる。
よくある誤解
定義式より、区間 \(x\in[0,1]\) の一様分布は
$$p(x)=1\left(=\frac{1}{1-0}\right)$$
で表される。
しかし、これはあくまで確率密度関数についての表現であり、「確率変数が、とある \(x\) の値をとる確率が1(100%)」の意味ではないことに注意せよ。
実際、
$$\int_{0}^{1}p(x)dx=\int_{0}^{1}1dx=[x]_{0}^{1}=1-0=1$$
が成り立つ。
確率変数と確率密度関数については

を参照のこと。


Comments