計算や理論を簡単にするために、積分計算においては、しばしば置換積分による変数変換をします。
とある関係式によって結ばれる変数どうしを入れ替えるためには、どのような操作が必要になるでしょうか?
この記事では1変数関数の不定積分における置換積分からはじめて、最後は多変数関数の定積分における置換積分まで、概念図を交えながら、その公式と原理を解説します。
1変数関数・不定積分の置換積分
公式
1変数関数の不定積分においては、以下の置換積分の公式が成り立ちます。
関数 \(y=f(x)\) において、 \(x\) が \(t\) の \(C^1\) 級関数 \(\phi(t)\) によって
$$x=\phi(t)$$
と表されるとき、
$$\int f(x)dx=\int f(\phi(t))\phi'(t)dt$$
である。
証明
$$y=F(x)=\int f(x)dx$$
とします。
\(F(x)\) に \(x=\phi(t)\) を代入して得られる式 \(y=F(\phi(t))\) を \(t\) で微分すると、
$$\frac{dy}{dt}=\frac{d}{dt}F(\phi(t))$$
$$\frac{dy}{dt}=\frac{d}{d\phi}F(\phi(t))\cdot\frac{d\phi}{dt}$$
$$\frac{dy}{dt}=F'(\phi(t))\cdot\phi'(t)$$
$$\frac{dy}{dt}=f(\phi(t))\cdot\phi'(t)$$
より
$$y=\int f(\phi(t))\phi'(t)$$
となります。
1変数関数・定積分の置換積分
公式
定積分の場合、置換積分の公式は以下のように変化します。
\(x=\phi(t),a=\phi(\alpha),b=\phi(\beta)\) のとき
$$\int_{a}^{b}f(x)dx=\int_{\alpha}^{\beta}f(\phi(t))\phi'(t)dt$$
この公式は不定積分の置換積分から直ちに導かれますが、多変数関数における置換積分を考える前の準備として、その原理を詳しく見ていきます。
変数変換における拡大率の考え方
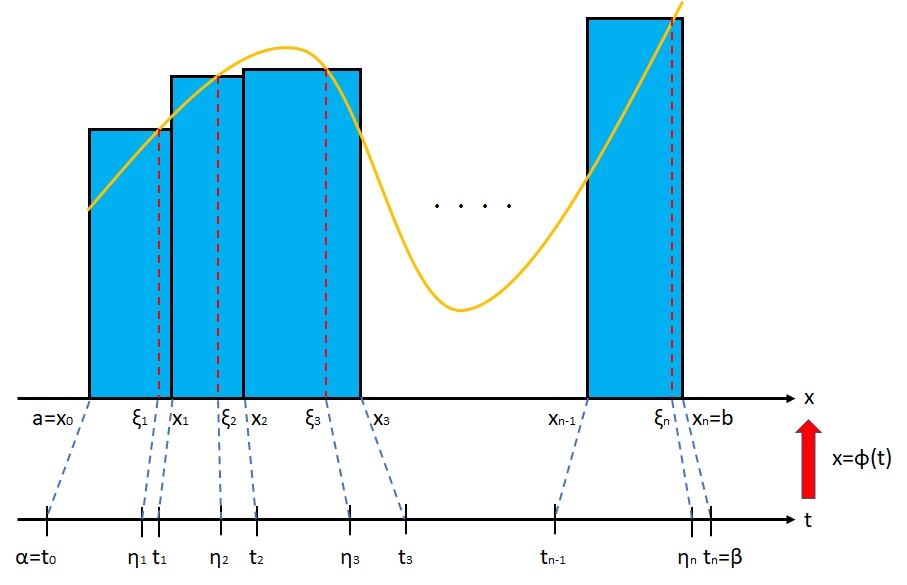
区間 \([a,b]\) における定積分は、上図に示すような階段状の長方形の面積の(正負を考慮した)和の極限値としての意味を持ちます。
変数変換 \(x=\phi(t)\) により、 \(a=\phi(\alpha),b=\phi(\beta)\) が成り立っているとき、
\(t\) の区間 \([\alpha,\beta]\) は \(x_k=\phi(t_k)\) を満たすような \(t_k\,(k=0,1,\cdots,n)\) 個の小区間に分割されていると考えることができます。
また、小区間 \([x_{k-1},x_k]\) 内に任意に取った点 \(\xi_k\) に対し、 \(\xi_k=\phi(\eta_k)\) を満たすような \(\eta_k\in[t_{k-1},t_k]\) が存在します。
ここで、微分係数の定義
$$\phi'(\eta_k)=\lim_{h\to 0}\frac{\phi(\eta_k)-\phi(\eta_k-h)}{h}$$
すなわち
$$\phi'(\eta_k)=\lim_{h\to 0}\frac{\phi(\eta_k)-\phi(\eta_k-h)}{t-(t-h)}$$
において
$$t\to t_k$$
$$t-h\to t_{k-1}$$
$$\phi(\eta_k)\to \phi(t_k)=x_k$$
$$\phi(\eta_{k-1})\to\phi(t_{k-1})=x_{k-1}$$
と置き換えて考えることにより、
小区間 \([t_{k-1},t_k]\) の長さは変換 \(\phi\) によってほぼ \(\phi'(\eta_k)\) 倍に拡大されるため、 \(x_k-x_{k-1}\simeq\phi'(\eta_k)(t_k-t_{k-1})\) とすることができます。
したがって
$$\sum_{k=1}^{n}f(\eta_k)(x_k-x_{k-1})\simeq\sum_{k=1}^{n}f(\phi(\eta_k))\phi'(\eta_k)(t_k-t_{k-1})$$
となります。
ここで、 \(n\to\infty\) とすると、左辺は \(\int_{a}^{b}f(x)dx\) 、右辺は \(\int_{\alpha}^{\beta}f(\phi(t))\phi'(t)dt\) に収束するため、
$$\int_{a}^{b}f(x)dx=\int_{\alpha}^{\beta}f(\phi(t))\phi'(t)dt$$
が導かれます。
以上の議論より、定積分の変数変換の際には次の作業が必要になります。
- \(x\) を \(\phi(t)\) に書き換える
- 拡大率 \(\phi'(t)\) を追加で掛ける
ここでいう拡大率は、「変換 \(x=\phi(t)\) により、小区間の長さが何倍に拡大されるか」を示しています。
多変数関数・定積分の置換積分
2変数関数の場合
2変数関数 \(f(x,y)\) に対し \(x=x(u,v),y=y(u,v)\) という変数変換を適用する場合、1変数関数における議論から
$$\int\int_{\Omega}f(x,y)dxdy=\int\int_{D}f(x(u,v),y(u,v))E(u,v)dudv$$
という式が成立することが予想できます。
このとき \(E(u,v)\) は拡大率をあらわします。
ただし、2変数関数の場合は小区間から小区間という直線の拡大率ではなく、 \(uv\) 平面上の領域 \(D\) 内の小さな面積が、 \(xy\) 平面上の領域 \(\Omega\) 内の小さな面積へと移されるときの「面積の拡大率」を意味しています。
したがって、以下この \(E(u,v)\) がどのように表現されるかについてみていきます。
\(uv\) 平面から \(xy\) 平面への1次変換と平行移動による面積の拡大率
はじめに、 \(uv\) 平面から \(xy\) 平面への変数変換が、1次変換と平行移動のみにより行われる場合を考えます。
つまりこのとき、
$$x=\alpha u+\beta v+\xi$$
$$y=\gamma u+\delta v+\eta$$
とあらわされます。
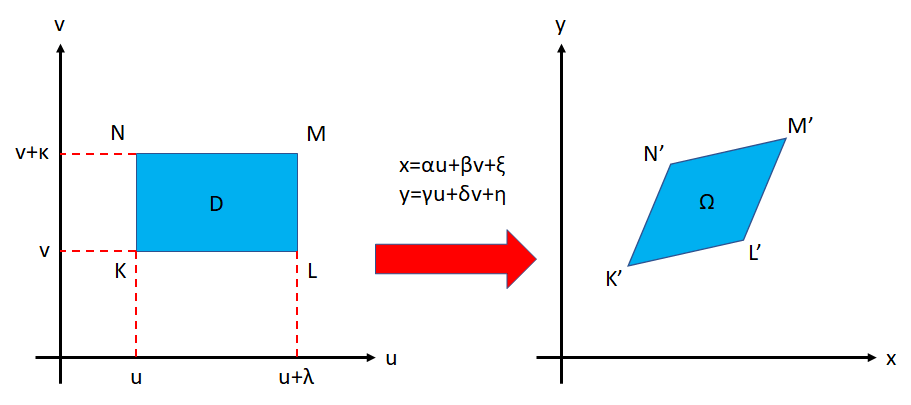
この場合、 \(D\) が4点 \(K(u_0,v_0)\) , \(L(u_0+\lambda,v_0)\) , \(M(u_0+\lambda,v_0+\kappa)\) , \(N(u_0,v_0+\kappa)\) を頂点に持つようなごく小さい長方形であるとすると、
これらの頂点が \(xy\) 平面に写された点 \(K',L',M',N'\) は、2つのベクトル \(\vec{K'L'}=(\alpha\lambda,\gamma\lambda),\vec{K'N'}=(\beta\kappa,\delta\kappa)\) によって張られる平行四辺形を形成します。
したがって、 \(\vec{K'L'}\) と \(\vec{K'N'}\) のなす角を \(\theta\) とすると、四角形 \(K',L',M',N'\) の面積 \(\mu(\Omega)\) は
$$\mu(\Omega)=|\vec{K'L'}|\cdot|\vec{K'N'}|\cdot\sin\theta$$
$$=|\vec{K'L'}|\cdot|\vec{K'N'}|\sqrt{1-\cos^2\theta}$$
$$=\sqrt{|\vec{K'L'}|^2\cdot|\vec{K'N'}|^2-(|\vec{K'L'}|\cdot|\vec{K'N'}|\cos\theta)^2}$$
$$=\sqrt{|\vec{K'L'}|^2\cdot|\vec{K'N'}|^2-\vec{K'L'}\cdot\vec{K'N'}}$$
$$=\sqrt{(\alpha^2+\gamma^2)(\beta^2+\delta^2)-(\alpha\beta+\delta\gamma)^2}\lambda\kappa$$
$$=\sqrt{(\alpha\delta-\beta\gamma)^2}\mu(D)=|\alpha\delta-\beta\gamma|\mu(D)$$
とあらわせます。
今回は \(D\) が長方形である場合を想定しましたが、 \(D\) が任意の形状である場合も \(D\) を細かい長方形の集合に分割することで同様の議論が成り立ちます。
よって、以下の定義が導かれます。
\(uv\) 平面から \(xy\) 平面への変数変換が、1次変換と平行移動のみによって行われるとき、
\(uv\) 平面上の領域 \(D\) の面積 \(\mu(D)\) と、それが写される \(xy\) 平面上の領域 \(\Omega\) の面積 \(\mu(\Omega)\) について、以下の関係式が成り立つ。
$$\mu(\Omega)=|\alpha\delta-\beta\gamma|\mu(D) \tag{1}$$
\(uv\) 平面から \(xy\) 平面への一般の変数変換による面積の拡大率
状況を一般化し、 \(x,y\) が \(u,v\) の \(C^1\) 級の関数として
$$x=x(u,v),y=y(u,v)$$
のように表される場合を考えます。
なお、この変換は1対1であるとします。
下図の領域 \(D\) と領域 \(\Omega\) は、この変換を図示したものです。
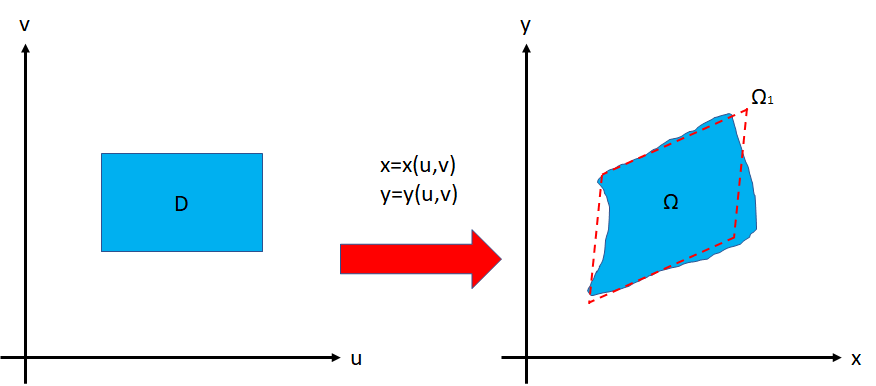
ここで、 \(x,y\) を \(u,v\) の1次式で近似します。
すなわち、関数 \(x(u,v),y(u,v)\) を領域 \(D\) 内の点 \((a,b)\) でのテイラー展開の1次までの項によって近似すると
$$x\simeq x(a,b)+\frac{\partial x(a,b)}{\partial u}(u-a)+\frac{\partial x(a,b)}{\partial v}(v-b)$$
$$=\frac{\partial x(a,b)}{\partial u}u+\frac{\partial x(a,b)}{\partial v}v+(定数)$$
$$y\simeq y(a,b)+\frac{\partial y(a,b)}{\partial u}(u-a)+\frac{\partial y(a,b)}{\partial v}(v-b)$$
$$=\frac{\partial y(a,b)}{\partial u}u+\frac{\partial y(a,b)}{\partial v}v+(定数)$$
となります。
この1次近似式により領域 \(D\) を \(xy\) 平面に写したものが、上図の赤点線で示した平行四辺形の領域 \(\Omega_1\) です。
このとき、領域 \(\Omega_1\) の面積を \(\mu(\Omega_1)\) とすると、 \(\mu(\Omega)\simeq\mu(\Omega_1)\) と考えることができます。
\((1)\) 式を使って計算すると、
$$\mu(\Omega)\simeq\mu(\Omega_1)=\left|\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\right|\mu(D)$$
となります。
ここで、
$$\left|\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\right|$$
のことをヤコビアン(記事末尾参照)といい、 \(\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\) であらわします。
すなわち、
$$\mu(\Omega)\simeq\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\mu(D) \tag{2}$$
です。
2変数関数・定積分の置換積分の公式
以上の議論を踏まえて、2変数関数の定積分における置換積分の公式を導きます。
\(uv\) 平面上の領域 \(D\) が \(n\) 個の小領域 \(D_1,D_2,\cdots,D_n\) に分割され、それぞれが変換 \(x=x(u,v),y=y(u,v)\) によって \(xy\) 平面上の小領域 \(\Omega_1,\Omega_2,\cdots,\Omega_n\) に写されていると考えます。
この小領域 \(\Omega_1,\Omega_2,\cdots,\Omega_n\) をすべて足し合わせたものが \(xy\) 平面上の領域 \(\Omega\) です。
各 \(D_k\) 上に任意の点 \((u_k,v_k)\) を取ると、変換 \(x_k=x_k(u_k,v_k),y_k=y_k(u_k,v_k)\) により、点 \((x_k,y_k)\) は \(\Omega_k\) 上の点となります。
ここで、 \((2)\) 式より、 \(\mu(\Omega_k)\simeq\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\mu(D_k)\) なので
$$f(x_k,y_k)\mu(\Omega_k)\simeq f(x_k(u_k,v_k),y_k(u_k,v_k))\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\mu(D_k)$$
が成り立ち、 \(n\) 個の小領域すべてについて足し合わせることで
$$\sum_{k=1}^{n}f(x_k,y_k)\mu(\Omega_k)\simeq\sum_{k=1}^{n}f(x_k(u_k,v_k),y_k(u_k,v_k))\left|\frac{\partial(x,y)}{\partial(u,v)}\right|\mu(D_k)$$
となります。
ここで、 \(n\to\infty\) とすると両辺の差は次第に小さくなり、左辺は \(\int\int_{\Omega}f(x,y)dxdy\) 、右辺は \(\int\int_{D}f(x(u,v),y(u,v))\left|\frac{\partial(x,y)}{\partial(u,v)}\right|dudv\) に収束します。
したがって、以下の定理が導かれます。
\(uv\) 平面上の領域 \(D\) が、変換
$$x=x(u,v),\,y=y(u,v)$$
(ただし、 \(x,y\) は \(u,v\) の \(C^1\) 級の関数)によって \(xy\) 平面上の領域 \(\Omega\) へ1対1に写されるとき、以下の式が成り立つ。
$$\int\int_{\Omega}f(x,y)dxdy=\int\int_{D}f(x(u,v),y(u,v))\left|\frac{\partial(x,y)}{\partial(u,v)}\right|dudv$$
多変数関数への応用
2変数関数の定積分における置換積分の公式を多変数関数一般に応用すると、次のようになります。
元々の \(n\) 次元座標 \({\bf x}=(x_1,x_2,\cdots,x_n)\) が、新しい座標 \({\bf y}=(y_1,y_2,\cdots,y_n)\) で、 \(x_i=x_i(y_1,y_2,\cdots,y_n)\) と書けているとき、以下の式が成り立つ。
$$\int_{A}f({\bf x})d{\bf x}=\int_{B}g({\bf y})\left|\frac{\partial {\bf x}}{\partial {\bf y}}\right|d{\bf y}$$
ただし、 \(B\) は新しい座標 \({\bf y}\) でみた積分領域 \(A\) のことであり、 \(g\) は対応する点での \(f\) の値を表す。
また、 \(d{\bf x}=dx_1dx_2\cdots dx_n,\,d{\bf y}=dy_1dy_2\cdots dy_n\) です。
(補足)ヤコビアンについて
ヤコビアン \(\frac{\partial {\bf x}}{\partial {\bf y}}\) は、ヤコビ行列
$$\begin{pmatrix} \frac{\partial x_1}{\partial y_1} & \frac{\partial x_1}{\partial y_2} & \cdots & \frac{\partial x_1}{\partial y_n} \\ \frac{\partial x_2}{\partial y_1} & \frac{\partial x_2}{\partial y_2} & & \vdots \\ \vdots & & \ddots & \vdots \\ \frac{\partial x_n}{\partial y_1} & \cdots & \cdots & \frac{\partial x_n}{\partial y_n}\end{pmatrix}$$
の行列式に相当します。


Comments