動機
乱数をたくさん発生させたとき、その最大値はどんなふうに分布することになるのか気になった。
問題
確率密度関数 \(f\) にしたがう連続確率変数 \(X\) を考える。独立に \(n\) 個のサンプルを発生させ、その最大値を \(Y\) とする。すなわち
$$Y=\mathrm{max}\{X_1, X_2, \ldots, X_n\}$$
とおく。この \(Y\) を連続確率変数と見たとき、これがしたがう確率密度関数 \(g\) を求めよ。
解答
\(f\) に対応する累積分布関数 \(F\) を用いると、 \(X\) の値が \(a\) 以下となる確率は、次のように表せる。
$$P(X\leq a)=\int_{-\infty}^{a}f(x)dx=F(a)$$
ここで \(X\) の定義域は \((-\infty,\infty)\) としているが、異なる場合でも以下同様の議論ができる。
また、 \(g\) に対応する累積分布関数 \(G\) を用いると、同様に \(Y\) の値が \(a\) 以下となる確率を表現できるが、これは \(F\) との関係から次のように書ける。
$$Q(Y\leq a)=G(a)=\left\{F(a)\right\}^{n}\tag{1}$$
なぜならば、 \(Y\) が \(a\) 以下であるとき、各 \(X_i\quad(i=1,2,\ldots,n)\) も \(a\) 以下であり、それらは独立事象であるためである。
確率密度関数と累積分布関数の関係から
$$f(x)=\frac{d}{dx}F(x)\tag{2}$$
$$g(x)=\frac{d}{dx}G(x)\tag{3}$$
より、 \((1)\) 式の変数を \(x\) として、後半部を \((3)\) 式に代入すると
$$g(x)=\frac{d}{dx}G(x)=\frac{d}{dx}\left\{F(x)\right\}^{n}$$
$$=\frac{dF(x)}{dx}\frac{d}{dF(x)}\left\{F(x)\right\}^{n}=nf(x)\left\{F(x)\right\}^{n-1}$$
となる。以上より、 \(Y\) の確率密度関数を、 \(X\) の確率密度関数と累積分布関数を用いて表すことができた。
実験
標準正規分布 \(\mathcal{N}(0, 1)\) から \(10\) 個の乱数を発生させたとき、その最大値がしたがう分布を考える。上記の議論より、
$$f(x)=\frac{1}{\sqrt{2\pi}}\mathrm{exp}\left(-\frac{1}{2}x^{2}\right)$$
$$F(x)=\frac{1}{2}\left\{1+\mathrm{erf}\left(\frac{1}{2}\right)\right\}$$
$$g(x)=10f(x)\left\{F(x)\right\}^{9}$$
と表せる。
Python環境では、正規分布はscipy.stats.normに実装されており、 \(f(x), F(x)\) はそれぞれ、.pdf(x), .cdf(x)の関数から得ることができる。
コード
ヒストグラムと確率分布を同時にプロットする方法については以下を参照のこと。
import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import norm
n = 10000
m = 10
x = np.random.normal(size=(n, m))
plt.hist(x.reshape(-1), bins=50)
plt.hist(x.reshape(-1), bins=50)
plt.savefig("all_dist.png")
def g(x):
return m * norm.pdf(x) * norm.cdf(x) ** (m - 1)
y = x.max(axis=1)
b = plt.hist(y, bins=50)
plt.plot(b[1], g(b[1]) * n * (b[1][1] - b[1][0]), label="g(x)")
plt.legend()
plt.savefig("dist.png")乱数全体の分布(10万=1万x10個)
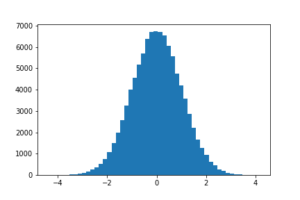
最大値の分布(1万個)
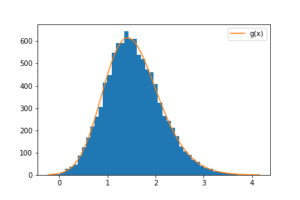

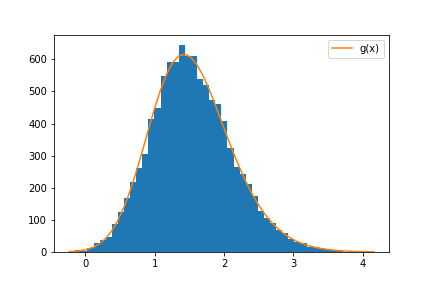
Comments