混同行列(Confusion Matrix)は、検査による分類結果をまとめた表です。
(「混合行列」ではないことに注意!)
この表を用いて感度や特異度、偽陽性/陰性率、陽性/陰性的中率、陽性/陰性尤度比などの指標を計算し、検査の性能を評価します。
この記事を読むことで、混同行列の見方と書き方を知り、そこから得られる指標の特性を理解して、検査や機械学習の性能を適切に評価することができるようになります。
混同行列の見方と書き方
混同行列とは?
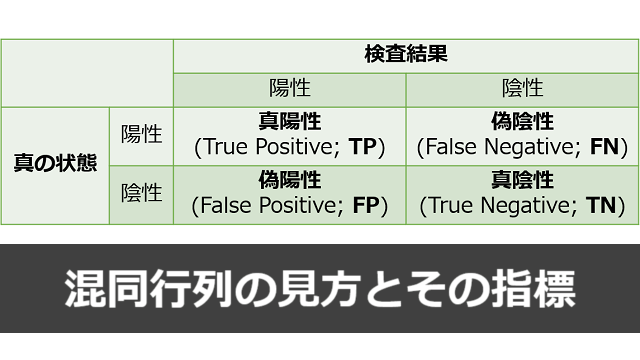
混同行列は、「検査結果の陽性/陰性」と「実際の(真の)陽性/陰性」について2×2の行列を作り、それぞれに該当する人数を書き込んだ表です。
混同行列の例
例として、以下のような検査を考えます。
A症候群という病気があり、その病気に対する新しい検査キットが開発された。
性能評価のために、A症候群の患者100人に実施すると、そのうち90人で陽性、10人で陰性となった。
また、健康な人1,000人を対象に実施すると、20人で陽性、980人で陰性となった。
この結果を混同行列であらわすと、以下のようになります。
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
混同行列内の数字の名前
この表の各セルには、以下の名前がついています。
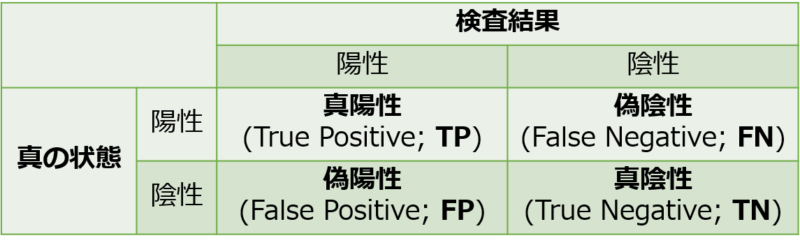
真陽性(True Positive; TP)
検査結果が陽性で、実際にも陽性であるべき人数。
真陰性(True Negative; TN)
検査結果が陰性で、実際にも陰性であるべき人数。
偽陽性(False Positive; FP)
検査で陽性と出たが、実際には陰性であるべきだった人数。
この場合、検査結果が「神経質すぎた」と評価できます。
このような間違いを第一種過誤といいます。
偽陰性(False Negative; FN)
検査で陰性と出たが、実際には陽性であるべきだった人数。
この場合、検査結果が「ザルすぎた」と評価できます。
このような間違いを第ニ種過誤といいます。
(補足)第一と第二種過誤ならどっちが問題?
病気の検査においては、第二種過誤の方がより問題視されることが多いです。
なぜならば、陽性が出た被験者に対して精密検査を行った結果、それが実は偽陽性であったことが判明しても「心配しすぎだった」で話が済むのに対し、
陰性と判断された被験者を放っておいたら実は病気で、気付いたら手遅れだったでは取り返しがつかなくなるためです。
混同行列から計算される指標
混同行列の情報から、検査に対する様々な指標を計算することができます。
それぞれ評価対象や使い勝手が異なりますので、以下
- 計算式
- A症候群についての計算例
- 評価している内容
- 性質(その指標を用いるべき・用いるべきでない状況)
の4つの視点から、
- 有病率
- 感度・特異度
- 偽陽性率・偽陰性率
- 陽性的中率・陰性的中率
- 陽性尤度比・陰性尤度比
の5つの指標を考えていくことにします。
有病率
英:Prevalence (Rate)
計算式
$$(有病率)=\frac{TP+FN}{TP+FN+FP+TN}$$
計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$(有病率)=\frac{90+10}{90+10+20+980}=\frac{100}{100+1000}\fallingdotseq 0.091$$
評価している内容
(一番はじめが検査性能と関係ない指標で申し訳ありませんが)検査を受けた人のうち、実際に陽性であるべき人の割合を示しています。
性質
「有病率」という言葉を使う場合には、検査を受けた人が全人口からランダムに選ばれていることを想定しています。
有病率が異常に高い(低い)場合、実際に陽性または陰性であるべき人の人数に大きな偏りが出ますが、このような状況では、これから紹介する指標がうまく機能しないことが多々あります。
具体的には、さほど性能が高くない検査に対しても、指標が非常に良い値を示しやすくなるので注意が必要です。
このようなデータを歪みの大きいデータといいます。
ここでは、歪みの大きいデータに対する検査性能の評価は難しいとだけ、覚えておいてください。
感度と特異度
英:Sensitivity / Specificity
計算式
$$(感度)=\frac{TP}{TP+FN}$$
$$(特異度)=\frac{TN}{TN+FP}$$
計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$(感度)=\frac{90}{90+10}=0.9$$
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$(特異度)=\frac{980}{20+980}=0.98$$
評価している内容
感度は「病気の人を正しく検出できる割合」、
特異度は「病気でない人を正しく除外できる割合」を評価します。
そのため、どちらも高いほうが良い検査を意味します。
性質
一般に、感度の高い検査は除外診断に、特異度の高い検査は確定診断に優れているとされています。
なぜならば、感度の高い検査(病気の患者の大部分を検出し、さらには健常人ですら「病気」と判断しうる、陽性が出やすい検査)でも陽性が出ない場合は、ほとんど病気ではないと考えてよく、
特異度の高い検査(陽性が出にくい検査)でも陽性が出る場合は、病気である可能性が非常に高いためです。
よって、実際の病気の診断においては、感度の高い検査(たとえば便潜血:大腸癌で陽性になりやすいが、痔など他の腸疾患でも陽性となる、など)でスクリーニングを行ったあと、
怪しいと判断された被験者に対し特異度の高い検査(たとえば内視鏡:大腸癌を視認しないと陽性にならない、など)を行って確定診断するという作戦をとります。
なお、感度は再現率(Recall)や真陽性率(TPR:True Positive Rate)、特異度は真陰性率(TNR: True Negative Rate)と呼ばれることもあります(後述)。
偽陽性率(FPR)と偽陰性率(FNR)
英:False Positive/Negative Rate
計算式
$$FPR=\frac{FP}{TN+FP}$$
$$FNR=\frac{FN}{TP+FN}$$
計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$FPR=\frac{20}{980+20}=0.020$$
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$FNR=\frac{10}{90+10}=0.100$$
評価している内容
偽陽性率(FPR)は「病気でない人に陽性が出てしまう割合」、
偽陰性率(FNR)は「病気の人に陰性が出てしまう割合」を評価しています。
これは、それぞれ第一種過誤・第二種過誤が生じる割合と考えることができます。
そのため、どちらも低いほうが良い検査を意味します。
性質
定義式から、それぞれ感度・特異度の逆として考えることができ、それぞれ
$$FPR=1-(特異度)$$
$$FNR=1-(感度)$$
という関係があります。
そのため、感度・特異度と似た特徴を持ち、同時にトレードオフの関係にもあります。
具体的には、検査の感度(=真陽性率; TPR)を上げようとすると、同時に偽陽性率(FPR)も上昇してしまいます。
指標間のトレードオフ関係をふまえ、検査を適切に評価する方法として、のちほどROC曲線を紹介します。
陽性的中率(PPV)と陰性的中率(NPV)
英:Positive/Negative Predictive Value
計算式
$$PPV=\frac{TP}{TP+FP}$$
$$NPV=\frac{FN}{TN+FN}$$
計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$PPV=\frac{90}{90+20}\fallingdotseq 0.818$$
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$NPV=\frac{980}{980+10}\fallingdotseq 0.990$$
評価している内容
陽性的中率(PPV)は「陽性と判定された人が実際に病気である割合」、
陰性的中率(NPV)は「陰性と判断された人が実際に病気でない割合」を評価しています。
そのため、どちらも高いほうが良い検査を意味します。
性質
感度・特異度とFPR/FNRが、病気のあり/なしを分母にしていたのに対し、
PPV/NPVは陽性/陰性を分母にしている点で視点が異なります。
その結果、感度・特異度とFPR/FNRに比べ、PPV/NPVは有病率の影響を受けて変化しやすいという性質があります。
具体例で考えてみましょう。
病気:健康の比が100:1,000であったA症候群のかわりに、病気:健康=100:10,000のB症候群についての検査を考えます。
A・B症候群の検査がともに同じの感度・特異度をもつとき、それぞれの混同行列は次のようになります。
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
| 検査陽性 | 検査陰性 | |
|---|---|---|
| B症候群である | 90 | 10 |
| B症候群でない | 200 | 9800 |
B症候群の混同行列に基づいてPPV/NPVを計算すると
$$PPV=\frac{90}{90+200}\fallingdotseq 0.310$$
$$NPV=\frac{9800}{9800+10}\fallingdotseq 0.999$$
となり、A症候群について \(PPV\fallingdotseq 0.818, NPV\fallingdotseq 0.990\) であったことを考えると、NPVの微増に対してPPVが大きく低下します。
A・B症候群の検査はともに、病気でない人に対して2%ずつしか偽陽性を出していないのですが、有病率が下がる(病気でない人が増える)と、その2%が意味する絶対数が増えます。
そのため、PPVの低下(偽陽性を出してしまう割合の上昇)を招いてしまったのです。
現実の世界では、有病率を反映した検査結果がその後の対応を左右するので、PPV/NPVは非常に重要な指標です。
ところが検査精度の指標として感度・特異度しか示されない場合も多く、その結果、
「感度・特異度が優れているので採用したが、
PPVが低すぎて、陽性と判断されてもほとんどが健康な人だった」
という、現場での有効性を正しく判断できないケースが多々あります。
また、PPVは適合率(Precision)とも呼ばれます。
PPVは感度(=再現率; Recall)とは直線的ではないもののトレードオフの関係があり、Recallを上げようとするとPrecisionは低下しやすくなります。
このトレードオフ関係をふまえ、検査を適切に評価する方法として、のちほどPR(Precision-Recall)曲線を紹介します。
陽性尤度比と陰性尤度比
英:Positive/Negative Likelihood Ratio
計算式
$$(陽性尤度比)=\frac{感度}{1-特異度}=\frac{感度}{偽陽性率}$$
$$(陽性尤度比)=\frac{1-感度}{特異度}=\frac{偽陰性率}{特異度}$$
計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$(陽性尤度比)=\frac{\frac{90}{90+10}}{1-\frac{980}{980+20}}=45$$
$$(陰性尤度比)=\frac{1-\frac{90}{90+10}}{\frac{980}{980+20}}\fallingdotseq 0.10$$
評価している内容
陽性尤度比が感度(真陽性率)と偽陽性率の比、陰性尤度比が特異度(真陰性率)と偽陰性率の比であることから、
陽性尤度比は「病気の人は病気でない人に比べて、何倍陽性と判定されやすいか」、
陰性尤度比は「病気の人は病気でない人に比べて、何倍陰性と判定されやすいか」を評価しています。
そのため、陽性尤度比が高く、陰性尤度比が低いとき、良い検査であることを意味します。
性質
陽性尤度比/陰性尤度比は、検査の結果を見た後に被検者が実際に病気である確率(=検査後確率)を求めるために使用されます。
検査前確率
「検査をする前に被験者が病気である確率」を検査前確率といいます。
これは有病率に等しくなります。
検査前オッズ
$$\frac{\mathrm{A}}{\mathrm{not A}}$$
の形をとる指標をオッズといいます。
これにもとづき、検査前オッズを
$$(検査前オッズ)=\frac{病気の人数}{病気でない人数}$$
と定義します。
これは有病率を用いると
$$(検査前オッズ)=\frac{有病率}{1-有病率}=\frac{TP+FN}{FP+TN}$$
と計算できます。
検査後オッズ
検査後オッズを
$$(検査後オッズ)=\frac{検査結果が〇性で、実際に病気の人数}{検査結果が〇性で、実際には病気でない人数}$$
と定義します。

$$(陽性の検査後オッズ)=\frac{TP}{FP}$$
$$(陰性の検査後オッズ)=\frac{FN}{TN}$$
ここで
$$(検査前オッズ)\times(陽性尤度比)=\frac{TP+FN}{FP+TN}\cdot\frac{\frac{TP}{TP+FN}}{\frac{FP}{FP+TN}}$$
$$=\frac{TP}{FP}=(陽性の検査後オッズ)$$
$$(検査前オッズ)\times(陰性尤度比)=\frac{TP+FN}{FP+TN}\cdot\frac{\frac{TN}{FP+TN}}{\frac{FN}{TP+FN}}$$
$$=\frac{TN}{FN}=(陰性の検査後オッズ)$$
より、検査前オッズに、検査の結果が
- 陽性であれば陽性尤度比
- 陰性であれば陰性尤度比
を掛けることで、検査後オッズを計算することができます。
検査後確率
「検査結果が〇性のとき、実際に病気である確率」を検査後確率といいます。
確率 \(p\) とオッズの間には
$$\mathrm{Odds}=\frac{p}{1-p}\Leftrightarrow p=\frac{\mathrm{Odds}}{1+\mathrm{Odds}}$$
という関係があるので、検査後オッズから検査後確率を求めることができます。
オッズ・確率の計算例
| 検査陽性 | 検査陰性 | |
|---|---|---|
| A症候群である | 90 | 10 |
| A症候群でない | 20 | 980 |
$$(検査前確率)=(有病率)=\fallingdotseq 0.091$$
$$(検査前オッズ)=\frac{90+10}{980+20}=0.1$$
より、検査結果が陽性の場合
$$(検査後オッズ)=(検査前オッズ)\times(陽性尤度比)=0.1\times 45=4.5$$
$$(検査後確率)=\frac{(検査後オッズ)}{1+(検査後オッズ)}=\frac{4.5}{1+4.5}\fallingdotseq 0.818$$
検査結果が陰性の場合
$$(検査後オッズ)=(検査前オッズ)\times(陰性尤度比)\fallingdotseq 0.1\times 0.1=0.010$$
$$(検査後確率)\fallingdotseq\frac{0.01}{1+0.01}\fallingdotseq 0.010$$
となります。
したがって、検査で陽性と判定された場合には被験者が病気である確率が上昇し、陰性と判定された場合には低下します。
また、以上の結果から、検査結果が陽性である場合の検査後確率は陽性的中率に等しく、
検査結果が陰性である場合の検査前確率は(1-陰性的中率)に等しいことがわかります。
すなわち、尤度比を用いずとも、混同行列があれば検査後確率を直接計算することも可能です。
尤度比とベイズの定理
上記のような尤度比を用いた検査後確率の計算は、ベイズの定理に基づくものです。

ベイズの定理から上記の計算法が導かれることの証明は、以下の記事を参照してください。

一般に、陽性尤度比は1より大きく、陰性尤度比は1より小さい正の値を取ることが予想されますが、万が一この条件を満たさない検査があったとしたら、それは無意味な検査であることを意味します。
指標間のトレードオフを評価する
混同行列は閾値で変化する
検査は通常なんらかの値を計測・計算し、それが閾値を超えているかどうかで陽性・陰性を判断します。
そのため、閾値を変化させることで結果も変わり、混同行列や各種指標の値も変化します。
具体的には、閾値をゆるくすると感度が上がり、厳しくすると特異度が高くなります。
このとき、次の2つの問題が生じます。
- これらの指標はトレードオフの関係にある
- 異なる検査どうしの性能比較が難しくなる
2番目については、「検査性能が閾値に依存するのであれば、『適切に』閾値を設定した『ダメな』検査と、閾値が『最適化されていない』『良い』検査は、どちらが優れているのか」ということが考えられます。
そもそも指標がトレードオフの関係にある中で、『適切な閾値』が何を意味するのか定かではありません。
この問題に対処するために、「閾値を最小から最大まで変化させたときのトレードオフを観察し、全閾値での性能で検査を評価する」という方法が用いられます。
以下、代表的な手法として、ROC曲線とPR曲線を紹介します。
ROC曲線
ROC曲線(Receiver Operating Characteristic Curve)は、感度(=真陽性率; TPR)と偽陽性率(FPR)のトレードオフをプロットした曲線です。
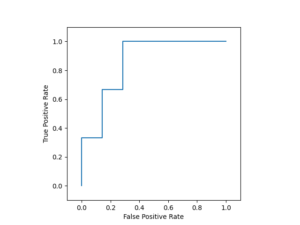
TPRを縦軸、FPRを横軸にプロットします。
感度(TPR)を上げるために閾値をゆるめると、FPRまで上昇してしまうので、ROC曲線は常に右肩上がりになります。
PR曲線
PR曲線(Precision Recall Curve)は、感度(=再現率; Recall)と陽性的中率(=適合率; Precision)のトレードオフをプロットした曲線です。
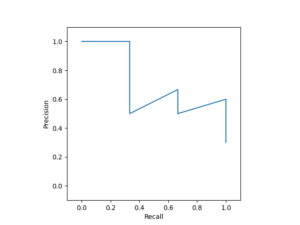
Precisionを縦軸、Recallを横軸にプロットします。
感度(Recall)を上げるために閾値をゆるめると、陽性的中率(Precision)は下がり気味になりますが、直接的な関係にはないため、右肩下がりを中心とした色々な形をとります。
AUCによる性能評価
ROC曲線やPR曲線を書いたあと、その性能はAUC(Area Under the Curve)で評価します。
AUCは、プロットの下にできる面積の大きさとして定義され、0(悪い)から1(良い)の値をとります。
一般的に、ROC曲線のAUC(ROC-AUC)が0.8を超えると良い検査といわれますが、PR曲線のAUCについては明確な基準がありません。
また、有病率の低い(歪みの大きい)データに対しては、ROC-AUCが不当に大きくなりやすいため、PR曲線を用いて評価した方が良いとも言われています。
こうしたROC曲線・PR曲線に関する詳細は、以下の記事で解説しています。


Comments