陽性尤度比・陰性尤度比は、検査の性能を評価する指標です。
検査前確率(有病率)と陽性(陰性)尤度比から、検査結果が陽性(陰性)であった場合に実際に病気である確率(検査後確率)を計算することができます。
この記事では、陽性尤度比・陰性尤度比を検査後確率の計算に使える理由について、ベイズの定理から導出します。
記号の意味
この記事では、以下のような記号を使用して、用語を表現します。
- 大文字のアルファベット:事象(「病気である」など)
- \(\lnot A\) :事象 \(A\) の否定(「病気である」→「病気でない」など)
- \(P(A)\) :事象 \(A\) が生じる確率
- \(P(A|B)\) :事象 (B) が生じた状態で事象 (A) が生じる条件付き確率
前提
陽性・陰性尤度比、検査前・検査後確率
陽性・陰性尤度比の定義や、検査前・検査後確率との関係については、以下の記事でくわしく説明しています。
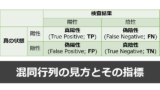
検査前・検査後確率を変形した検査前・検査後オッズと尤度比の間には、以下の関係があります。
$$(陽性の検査後オッズ)=(検査前オッズ)\times(陽性尤度比)$$
$$(陰性の検査後オッズ)=(検査前オッズ)\times(陰性尤度比)$$
条件付き確率・ベイズの定理
条件付き確率やベイズの定理
$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$
については、以下の記事でくわしく解説しています。

尤度比や検査前後の確率を記号であらわす
以下のように、事象を2つ定義します。
- \(A\) :病気である
- \(B\) :検査陽性である
このとき、検査前後の確率やオッズは次のように表現できます。
\((検査前確率)=P(A)\)
\((陽性の検査後確率)=P(A|B)\)
\((陰性の検査後確率)=P(A|\lnot B)\)
\((検査前オッズ)=\frac{P(A)}{P(\lnot A)}\)
\((陽性の検査後オッズ)=\frac{P(A|B)}{P(\lnot A|B)}\)
\((陰性の検査後オッズ)=\frac{P(A|\lnot B)}{P(\lnot A|\lnot B)}\)
また、検査の感度(病気の人を陽性と判定できる確率)と
特異度(病気でない人を陰性と判定できる確率)は次のように書けます。
- \((感度)=P(B|A)\)
- \((特異度)=P(\lnot B|\lnot A)\)
したがって、陽性・陰性尤度比は
- \((陽性尤度比)=\frac{感度}{1-特異度}=\frac{P(B|A)}{1-P(\lnot B|\lnot A)}=\frac{P(B|A)}{P(B|\lnot A)}\)
- \((陰性尤度比)=\frac{1-感度}{特異度}=\frac{1-P(B|A)}{P(\lnot B|\lnot A)}=\frac{P(\lnot B|A)}{P(\lnot B|\lnot A)}\)
と、あらわせます。
ベイズの定理から見た尤度比
陽性の検査後確率 \(P(A|B)\) とその否定 \(P(\lnot A|B)\) について、ベイズの定理より
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
$$P(\lnot A|B)=\frac{P(B|\lnot A)P(\lnot A)}{P(B)}$$
が成り立ちます。
辺々を割ると、
$$\frac{P(A|B)}{P(\lnot A|B)}=\frac{P(B|A)}{P(B|\lnot A)}\frac{P(A)}{P(\lnot A)}$$
$$(陽性の検査後オッズ)=(陽性尤度比)\times(検査前確率)$$
の関係が導かれます。
同様に、陰性の検査後確率 \(P(A|\lnot B)\) とその否定 \(P(\lnot A|\lnot B)\) について、ベイズの定理より
$$P(A|\lnot B)=\frac{P(\lnot B|A)P(A)}{P(\lnot B)}$$
$$P(\lnot A|\lnot B)=\frac{P(\lnot B|\lnot A)P(\lnot A)}{P(\lnot B)}$$
が成り立ちます。
辺々を割ると、
$$\frac{P(A|\lnot B)}{P(\lnot A|\lnot B)}=\frac{P(\lnot B|A)}{P(\lnot B|\lnot A)}\frac{P(A)}{P(\lnot A)}$$
$$(陰性の検査後オッズ)=(陰性尤度比)\times(検査前確率)$$
の関係が導かれます。
以上より、尤度比の定義からスタートして、検査前後の確率やオッズとの関係を導出することができました。


Comments