誤差楕円（確率長円）とは？計算方法とPythonによるプロット

誤差楕円（確率長円）は、２次元正規分布の分散を図示した楕円です。

正規分布の分散共分散行列から、任意の範囲をカバーする楕円の式を計算することができます。

この記事では、PythonのMatplotlibでの描画を例に、楕円の計算方法を解説します。

誤差楕円（確率長円）

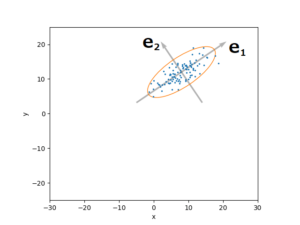
\(x,y\) の２次元空間に正規分布するデータを考えます。

正規分布の中心（平均）から、データの散らばる範囲を楕円で表示したものを誤差楕円（確率長円）といいます。

誤差楕円（確率長円）は、データ全体の何％を覆うように描画するかによって大きさを決定します。

その際、楕円の式は、正規分布の分散共分散行列を対角化する計算によって求められます。

matplotlib.patches.Ellipse

Pythonで楕円を描画するためにはmatplotlib.patches.Ellipseを使用します。

この関数では、主に以下のパラメータを指定する必要があるため、分布の式からこれらの値を計算します。

例

以下、具体的な分布を考えながら計算例を示します。

計算

平均 \(\boldsymbol{\mu}=(8, 12)\) 、分散共分散行列

$$\boldsymbol{\Sigma}=\begin{pmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{xy} & \sigma_y^2 \end{pmatrix}=\begin{pmatrix} 16 & \sqrt{78} \\ \sqrt{78} & 9 \end{pmatrix}$$

で表される２次元正規分布の誤差楕円（確率長円）を描画します。

分散共分散行列を対角化すると、対角化後の分散共分散行列は

$$\boldsymbol{\Sigma}'=\begin{pmatrix} \sigma_u^2 & 0 \\ 0 & \sigma_v^2 \end{pmatrix}$$

と書けます。ここで

$$\sigma_u^2=\frac{(\sigma_x^2+\sigma_y^2)+\sqrt{(\sigma_x^2-\sigma_y^2)^2+4\sigma_{xy}^2}}{2}$$

$$=\frac{(16+9)+\sqrt{(16-9)^2+4\cdot78}}{2}=44/2=22$$

$$\sigma_v^2=\frac{(\sigma_x^2+\sigma_y^2)-\sqrt{(\sigma_x^2-\sigma_y^2)^2+4\sigma_{xy}^2}}{2}$$

$$=\frac{(16+9)-\sqrt{(16-9)^2+4\cdot78}}{2}=6/2=3$$

です。

分散共分散行列を対角化する方法については、以下の記事で詳しく解説しています。

分散共分散行列の対角化（２次元）

概要 この記事では、分散共分散行列が対角行列となるように変数変換を行う方法、もしくは分散の方向が独立となるような軸の見つけ方について解説し、その導出を行う。 これは、主成分分析（Principal Component Analysis; P...

ushitora.net

2023.08.10

また、この対角化に対応する基底ベクトルは

$$\mathbf{e}_1=\left(1,\frac{\sigma_u^2-\sigma_x^2}{\sigma_{xy}}\right)=\left(1,\frac{22-16}{\sqrt{78}}\right)=\left(1,\frac{6}{\sqrt{78}}\right)$$

$$\mathbf{e}_2=\left(1,\frac{\sigma_v^2-\sigma_x^2}{\sigma_{xy}}\right)=\left(1,\frac{3-16}{\sqrt{78}}\right)=\left(1,-\frac{13}{\sqrt{78}}\right)$$

となります。

基底ベクトル \(\mathbf{e}_1,\mathbf{e}_2\) に沿って変数変換を行った \(u-v\) 平面において、分布に対応する楕円の式は

$$\frac{u^2}{\sigma_u^2}+\frac{v^2}{\sigma_v^2}=c^2\tag{1}$$

と書けます。

変数 \(\frac{u}{\sigma_u}\) と \(\frac{v}{\sigma_v}\) は標準正規分布にしたがうため、その２乗和 \(c^2\) は自由度２のカイ２乗分布にしたがいます。

１次元正規変数の平方和がしたがう分布【カイ二乗分布】の導出

独立の正規分布にしたがう確率変数を複数用意し、それらを２乗して足し合わせて新たな確率変数を作ったとき、その変数はカイ二乗分布にしたがう。この記事では、確率変数の変換にともなう確率密度関数の変換公式を出発点にして、平方和とカイ二乗分布の関係を導出する。

ushitora.net

2023.09.14

以下、自由度２のカイ２乗分布における累積分布関数 \(P\)（楕円が覆うデータの割合）と、 \(c^2\) ならびに \(c\) の関係について表示します。

これらの中から、誤差楕円（確率長円）を用いて表示したい分布の範囲に対応した \(c^2\) ならびに \(c\) の値を選択します。

\((1)\) 式において \(v=0\) のとき

$$\frac{u^2}{\sigma_u^2}=c^2\Leftrightarrow u=\pm c\sigma_u$$

同様に \(u=0\) のとき

$$\frac{v^2}{\sigma_v^2}=c^2\Leftrightarrow v=\pm c\sigma_v$$

より、楕円の長半径・短半径の長さはそれぞれ \(c\sigma_u, c\sigma_v\) となります。

したがって、楕円の長軸（width）・短軸（height）の長さは、それぞれ倍の \(2c\sigma_u, 2c\sigma_v\) です。

例えば \(P=0.950\) のとき

$$2c\sigma_u=2\cdot 2.448\cdot\sqrt{22}\simeq 22.96$$

$$2c\sigma_v=2\cdot 2.448\cdot\sqrt{3}\simeq 8.480$$

となります。

最後に楕円の傾き角として、長軸（ \(\mathbf{e}_1\) ）と \(x\) 軸がなす角度を求めます。

$$\mathbf{e}_1=\left(1,\frac{6}{\sqrt{78}}\right)$$

より、このベクトルと \(x\) 軸がなす角度を \(\theta\) とおくと

$$\tan\theta=\frac{6}{\sqrt{78}}$$

です。

よって

$$\theta=\arctan\left(\frac{6}{\sqrt{78}}\right)\simeq34.19^\circ$$

（ \(\arctan\) がラジアンで返される場合には、度に修正する）

以上より、今回は楕円のパラメータを次のように指定します。

コード

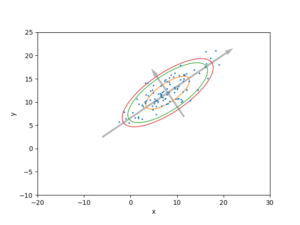
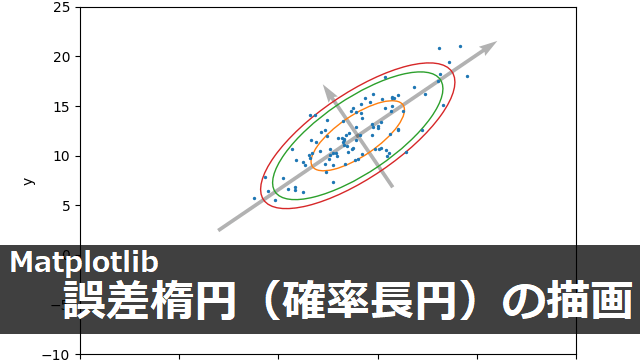
下のコードでは、範囲の50％（橙）、90％（緑）、95％（赤）を覆う誤差楕円（確率長円）を、基底ベクトルの軸とともにプロットしています。

\(P=0.500, P=0.900\) のときのwidth, heightも、 \(P=0.950\) のときと同様に計算できます。