この記事では、PythonのMatplotlibを用いて、XとYの2種類の値をとる2次元変数(X, Y)についての2次元ヒストグラムを、3次元空間に立体的に表示する方法を説明する。その方法を用いれば、この記事のアイキャッチ画像のようなグラフを作成することができる。
サンプルコード
この記事で使用するサンプルコードの全体図は以下の通りである。
import numpy as np
np.random.seed(42) # 乱数を固定
z = np.random.randn(2,50) # x,yの値を50個ずつ作成
hist, xedges, yedges = np.histogram2d(z[0], z[1], bins=5) # 5個区切りでxとyのヒストグラムを作成
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1]) # x,y座標を3D用の形式に変換(その1)
zpos = 0 # zは常に0を始点にする
dx = xpos[0][1] - xpos[0][0] # x座標の幅を設定
dy = ypos[1][0] - ypos[0][0] # y座標の幅を設定
dz = hist.ravel() # z座標の幅は棒の長さに相当
xpos = xpos.ravel() # x座標を3D用の形式に変換(その2)
ypos = ypos.ravel() # y座標を3D用の形式に変換(その2)
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure() # 描画領域を作成
ax = fig.add_subplot(111, projection="3d") # 3Dの軸を作成
ax.bar3d(xpos,ypos,zpos,dx,dy,dz) # ヒストグラムを3D空間に表示
plt.title("Histogram 2D") # タイトル表示
plt.xlabel("X") # x軸の内容表示
plt.ylabel("Y") # y軸の内容表示
ax.set_zlabel("Z") # z軸の内容表示
plt.show()まずはデータの準備
まず、例として使用するためのデータを作成する。
import numpy as np
np.random.seed(42) # 乱数を固定
z = np.random.randn(2,50) # x,yの値を50個ずつ作成ここではNumpyの乱数生成機能を用いて、標準正規分布に従うx, yの値を50個ずつ生成した。すなわち、z[0]がx、z[1]がyの値に相当し、同じ列にあるデータはセットとして扱う。
基準となる2次元ヒストグラムを作成
実際にグラフを3次元空間に表示するためには、後ほどちょっとした作業が必要となるが、ひとまず描画されるグラフのもととなる2次元ヒストグラムを作成する。
hist, xedges, yedges = np.histogram2d(z[0], z[1], bins=5) # 5個区切りでxとyのヒストグラムを作成
# hist = [[0. 1. 5. 1. 2.]
# [1. 1. 4. 6. 1.]
# [1. 1. 3. 2. 8.]
# [0. 0. 4. 4. 1.]
# [0. 0. 1. 3. 0.]]
# xedges = [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852 1.85227818]
# yedges = [-2.6197451 -1.78286735 -0.9459896 -0.10911185 0.7277659 1.56464366]np.histogram2dにx(z[0])とy(z[1])の値を与えてヒストグラムを作成する。このとき、binsを指定することでヒストグラムの棒の数を決めることができる(今回は5×5)。
返り値のhistはヒストグラムの棒の高さを表している。すなわち、3次元空間に描画されたヒストグラムを上(Z軸方向)から眺めている状態である。また、xedgesとyedgesは各棒の区切りとなる位置の座標を表している。
x, y座標の変換(その1)
上で得られたヒストグラムを3次元空間に表示するためには、x,y座標の配列を変形する必要がある。
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1]) # x,y座標を3D用の形式に変換(その1)
zpos = 0 # zは常に0を始点にする
# xpos = [[-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]
# [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]
# [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]
# [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]
# [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]]
# ypos = [[-2.6197451 -2.6197451 -2.6197451 -2.6197451 -2.6197451 ]
# [-1.78286735 -1.78286735 -1.78286735 -1.78286735 -1.78286735]
# [-0.9459896 -0.9459896 -0.9459896 -0.9459896 -0.9459896 ]
# [-0.10911185 -0.10911185 -0.10911185 -0.10911185 -0.10911185]
# [ 0.7277659 0.7277659 0.7277659 0.7277659 0.7277659 ]]np.meshgridを用いて、1次元配列のxedgesとyedgesから、histの次元に等しい配列の座標を作成する。その結果、xposは各行の値がxedges[:-1]に等しく、yposは各列の値がyedges[:-1]に等しい配列となる。このとき、xedgesとyedgesの両方において最後の要素を無視しているが、この理由は以下の図によって説明される。
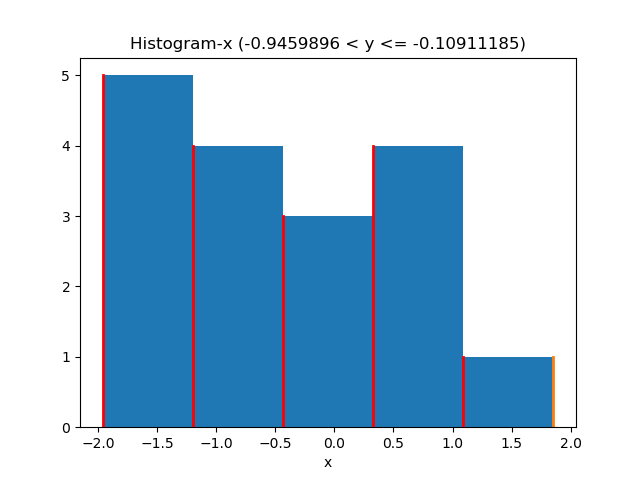
すなわち、棒の区切りを表したxedges(またはyedges)の6つの値のうち、棒の左側を指しているのは前の5本だけであり、最後の1本は棒の右側の座標を指定している。ヒストグラムの描画は、棒の左側の座標さえわかれば可能であるため、ここでは最後の要素を使用しないのである。
なお、zposは棒の根元のz座標のことであり、常に0として設定したいので、配列ではなく数値で指定してやればよい。
棒の幅を指定する
dx = xpos[0][1] - xpos[0][0] # x座標の幅を設定
dy = ypos[1][0] - ypos[0][0] # y座標の幅を設定
dz = hist.ravel() # z座標の幅は棒の長さに相当
# dx = 0.7623896616777428
# dy = 0.8368777519807502
# dz = [0. 1. 5. 1. 2. 1. 1. 4. 6. 1. 1. 1. 3. 2. 8. 0. 0. 4. 4. 1. 0. 0. 1. 3. 0.]今度はヒストグラムの棒の幅dx, dyを指定する。xedges・yedgesならびにそこから作成したxpos・yposの数値の間隔は一定になっているため、適当な連続した数値を2つ選んで差を求めてやればよい。この棒の幅もすべての棒において一定値をとるため、数値で指定できる。このとき、連続した数値の差に0.5、0.75などの数値をかけてやると、棒の間に隙間のあるヒストグラムを作成することができる。
z軸についての幅であるdzは、ヒストグラムの棒の長さを意味する。そのため、棒ごとに長さは異なるので配列で指定する。最終的な描画は1次元配列で行うため、hist.ravel()を用いて2次元配列のhistを1次元配列に変形する。
x, y座標の変換(その2)
上で述べた通り、最終的な描画は1次元配列の引数を取る関数によって行われるため、xposとyposも、ravel()を用いて1次元配列に変換する。
xpos = xpos.ravel() # x座標を3D用の形式に変換(その2)
ypos = ypos.ravel() # y座標を3D用の形式に変換(その2)
# xpos = [-1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852 ... -1.95967012 -1.19728046 -0.4348908 0.32749886 1.08988852]
# ypos = [-2.6197451 ... -2.6197451 -1.78286735 ... -1.78286735 -0.9459896 ... -0.9459896 -0.10911185 ... -0.10911185 0.7277659 ... 0.7277659 ]3次元空間への描画
最後に、必要なモジュールをインポートして3次元空間に描画する。
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure() # 描画領域を作成
ax = fig.add_subplot(111, projection="3d") # 3Dの軸を作成
ax.bar3d(xpos,ypos,zpos,dx,dy,dz) # ヒストグラムを3D空間に表示
plt.title("Histogram 2D") # タイトル表示
plt.xlabel("X") # x軸の内容表示
plt.ylabel("Y") # y軸の内容表示
ax.set_zlabel("Z") # z軸の内容表示
plt.show()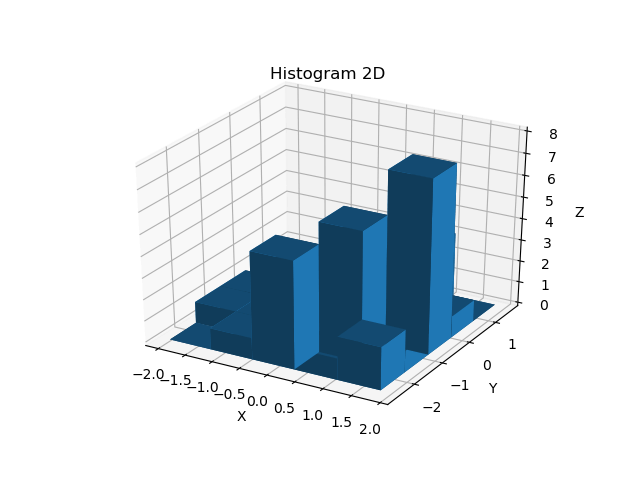
figとaxを指定した後、ax.bar3dに1次元配列(または数値)を引数に与えて描画することで、3次元空間の2次元ヒストグラムが得られる。

Comments