Matplotlibによる3Dプロット（簡単に）

Index

概要
3Dプロットの基本（最小限）
コード例
少しだけメッシュの解説
参考

概要

以前

この記事では、PythonのMatplotlibを用いて、XとYの２種類の値をとる２次元変数（X, Y）についての２次元ヒストグラムを、３次元空間に立体的に表示する方法を説明する。その方法を用いれば、この記事のアイキャッチ画像のようなグラフ...

等でMatplotlibを用いた３次元プロットについて述べたが、詳しい理屈は置いておいて、とりあえず図が書きたいという読者のために簡略版記事を作成した。

もっと複雑なことがしたい場合は、末尾に参考リンクを載せておいたのでそちらを参照してほしい。

3Dプロットの基本（最小限）

x軸, y軸を作る（ともに１次元）
X, Y = np.meshgrid(x, y)で２次元メッシュX, Yを作る
X, Yを用いて、関数Z=f(X, Y)を入力する

コード例

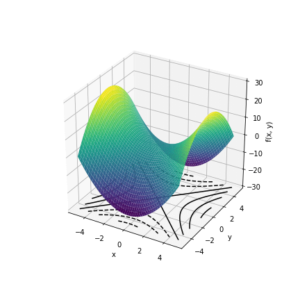
\(f(x, y)=x^2-y^2\) を図示し、等高線を表示した。

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 描画エリアの作成
fig = plt.figure(figsize=(6, 6))
# 3Dを指定
ax = fig.add_subplot(111, projection="3d")

# 各軸の設定
ax.set_xlabel("x", size=10)
ax.set_ylabel("y", size=10)
ax.set_zlabel("f(x, y)", size=10)
ax.set_zlim(-30, 30)

# x軸、y軸の作成
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)

# メッシュの作成
X, Y = np.meshgrid(x, y)
# 関数の入力
Z = X**2 - Y**2

# 曲面の描画
ax.plot_surface(X, Y, Z, cmap="viridis")
# 等高線の表示（z軸の最下部に合わせる）
ax.contour(X, Y, Z, colors="black", offset=-30)
plt.show()

少しだけメッシュの解説

X, Y = np.meshgrid(x, y)は、１次元配列

x = [0, 1, 2]
y = [3, 4]

から

# 本当はnp.ndarray
X = [
    [0, 1, 2],
    [0, 1, 2]
]
Y = [
    [3, 3, 3],
    [4, 4, 4]
]

のような２次元配列を作ってくれる。

これらを合わせると

X/Y	X1	X2	X3
Y1	(0, 3)	(1, 3)	(2, 3)
Y2	(0, 4)	(1, 4)	(2, 4)

となり、x軸・y軸からなる２次元平面が構成されていることがわかる。

あとはこれを用いて、２変数関数を表現することができる。

参考

ヒストグラムを表示したいとき

matplotlibで３次元空間に２次元ヒストグラムを表示する方法

空間に線や面を描きたい、重ねて表示したいとき

Matplotlibで３次元空間に円を描画、透過、境界を描画、線を引く

この記事では、PythonのMatplotlibを使用して３次元空間に球や面、線などを描画する方法について解説する。なお、ここで作成した画像の一部はにおいて利用されている。球体の描画基本球を描画するには、極座標の考え方を利用する必要...

概要

3Dプロットの基本（最小限）

コード例

少しだけメッシュの解説

参考

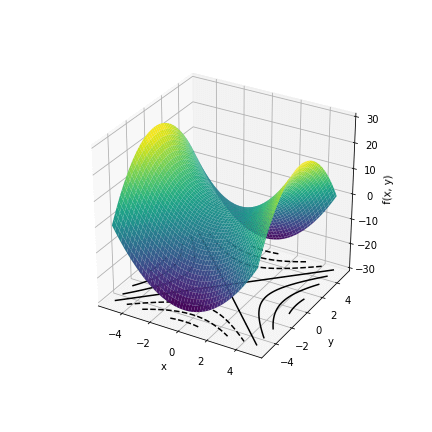
Comments