この記事では、PythonのMatplotlibを使用して3次元空間に球や面、線などを描画する方法について解説する。なお、ここで作成した画像の一部は

において利用されている。
球体の描画
基本
球を描画するには、極座標の考え方を利用する必要がある。直交座標 \(x,y,z\) を極座標 \(r,\theta_1,\theta_2\) に変換するときには
$$x_1 = r\cos{\theta_2}\sin{\theta_1}$$
$$x_2 = r\sin{\theta_2}\sin{\theta_1}$$
$$x_3 = r\cos{\theta_1}$$
の対応関係を用いる。
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
r = 3 # 半径を指定
theta_1_0 = np.linspace(0, np.pi/2, 100) # θ_1は[0,π/2]の値をとる
theta_2_0 = np.linspace(0, np.pi/2, 100) # θ_2は[0,π/2]の値をとる
theta_1, theta_2 = np.meshgrid(theta_1_0, theta_2_0) # 2次元配列に変換
x = np.cos(theta_2)*np.sin(theta_1) * r # xの極座標表示
y = np.sin(theta_2)*np.sin(theta_1) * r # yの極座標表示
z = np.cos(theta_1) * r # zの極座標表示
fig = plt.figure() # 描画領域を作成
ax = fig.add_subplot(111, projection="3d") # 3Dの軸を作成
ax.plot_surface(x,y,z) # 球を3次元空間に表示
plt.xlim([0,3])
plt.ylim([3,0]) # Y軸の表示は初期値とは逆にする
ax.set_zlim([0,3])
plt.xlabel("X")
plt.ylabel("Y")
ax.set_zlabel("Z")
plt.show()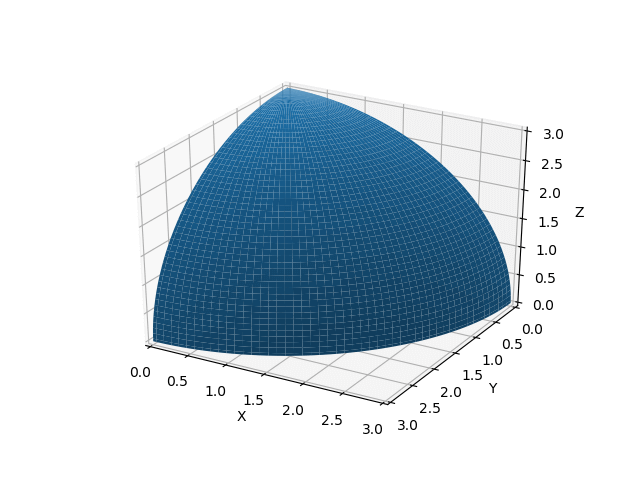
np.linspaceで \([0,\frac{\pi}{2}]\) の値をとる (\theta_1,\theta_2\) の値を100個ずつ生成する。そして、球を3次元空間に描画するax.plot_surfaceは引数に2次元配列をとるので、np.meshgridを用いて \(\theta_1,\theta_2\) 配列の形状を変換する。これを用いて \(x,y,z\) を計算すると、 \(x,y,z\) も2次元配列として得られる。
最後に描画領域と3D軸を作成してax.plot_surfaceで描画すると、上図のような半径 \(r\) の \(\frac{1}{8}\) 円が得られる。
np.meshgridについての詳細は以下を参照のこと。

以下、上記のコードと異なる部分のみを掲載する。
透過
ax.plot_surface(x,y,z, alpha=0.2) # 球を3次元空間に表示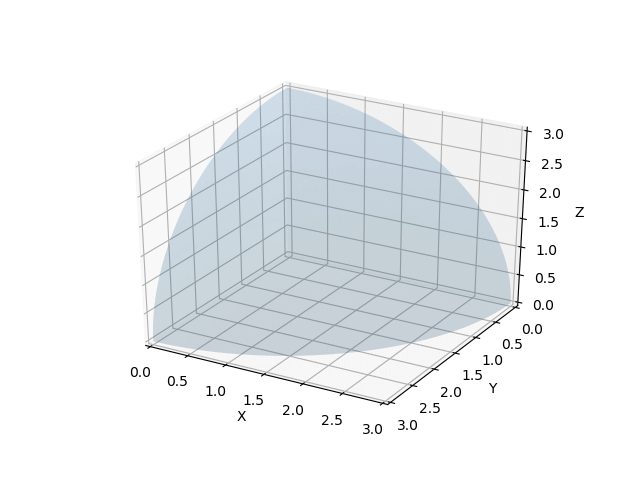
ax.plot_surfaceを用いて描画する際に、alpha値を指定することで描画図形を透過することができる。このalpha値は0~1の間で指定することができ、1に近い値をとるほど濃く描画される。
領域と境界の描画
続いて、 \(r,\theta_1,\theta_2\) をそれぞれ \([r,r+dr], [\phi_1,\phi_1+d\phi_1], [\phi_2,\phi_2+d\phi_2]\) の範囲で動かしたときに得られる領域を描画する。このコードの例では、具体的な値として \(r=3, dr=0.3, \phi_1=\phi_2=\frac{\pi}{12}, d\phi_1=d\phi_2=\frac{\pi}{12}\) を代入している。
phi_1 = np.linspace(np.pi/12*1, np.pi/12*2, 50) # φ_1は[π/12,π/6]の値をとる
phi_2 = np.linspace(np.pi/12*1, np.pi/12*2, 50) # φ_2は[π/12,π/6]の値をとる
phi_1_0, phi_2_0 = np.meshgrid(phi_1, phi_2) # 2次元配列に変換
x_p = np.cos(phi_2_0)*np.sin(phi_1_0) * r # xの極座標表示
y_p = np.sin(phi_2_0)*np.sin(phi_1_0) * r # yの極座標表示
z_p = np.cos(phi_1_0) * r # zの極座標表示
dr = 0.3
x_dp = np.cos(phi_2_0)*np.sin(phi_1_0) * (r + dr) # xの極座標表示
y_dp = np.sin(phi_2_0)*np.sin(phi_1_0) * (r + dr) # yの極座標表示
z_dp = np.cos(phi_1_0) * (r + dr) # zの極座標表示
r_b = np.linspace(r, r+dr, 50) # 半径を[r,r+dr]まで動かす
phi_12_1_1, r_b_12_1_1 = np.meshgrid(phi_1, r_b)
x_12_1_1 = np.cos(np.pi/12*1)*np.sin(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
y_12_1_1 = np.sin(np.pi/12*1)*np.sin(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
z_12_1_1 = np.cos(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
phi_12_1_2, r_b_12_1_2 = np.meshgrid(phi_2, r_b)
x_12_1_2 = np.cos(phi_12_1_2)*np.sin(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
y_12_1_2 = np.sin(phi_12_1_2)*np.sin(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
z_12_1_2 = np.cos(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
phi_12_2_1, r_b_12_2_1 = np.meshgrid(phi_1, r_b)
x_12_2_1 = np.cos(np.pi/12*2)*np.sin(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
y_12_2_1 = np.sin(np.pi/12*2)*np.sin(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
z_12_2_1 = np.cos(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
phi_12_2_2, r_b_12_2_2 = np.meshgrid(phi_2, r_b)
x_12_2_2 = np.cos(phi_12_2_2)*np.sin(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
y_12_2_2 = np.sin(phi_12_2_2)*np.sin(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
z_12_2_2 = np.cos(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
ax.plot_surface(x_p,y_p,z_p, color="g") # 半径rの球の一部を3次元空間に表示
ax.plot_surface(x_dp,y_dp,z_dp, color="g") # 半径r+drの球の一部を3次元空間に表示
ax.plot_surface(x_12_1_1,y_12_1_1,z_12_1_1, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_1_2,y_12_1_2,z_12_1_2, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_2_1,y_12_2_1,z_12_2_1, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_2_2,y_12_2_2,z_12_2_2, color="g") # 境界を3次元空間に表示https://ushitora.net/wp-content/uploads/2019/02/sphere3.png
np.linspaceで \([\frac{\pi}{12},\frac{\pi}{6}]\) の範囲を動く \(\phi_1, \phi_2\) を新たに作成する。コードの第1・第2ブロックでは、この \(\phi_1, \phi_2\) を用いて、半径が \(r=3\) のときと \(r+dr=3.3\) のときの球の一部を描画している。
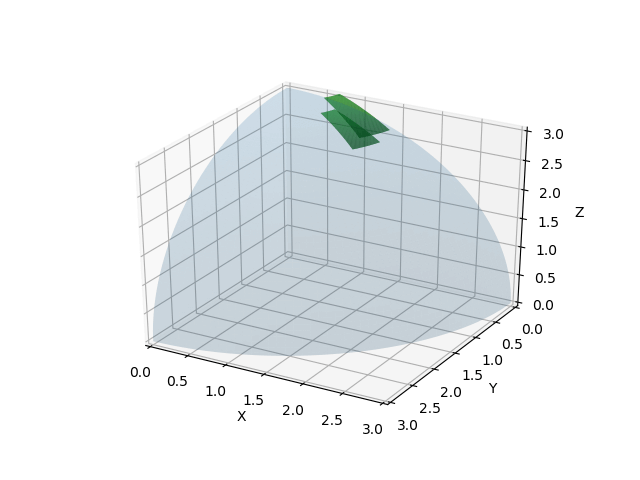
あとはこの2曲面を底面とした場合の4つの側面を描画すればよいのであるが、そのためには再びnp.linspaceを用いて、 \([3.0,3.3]\) の区間を動く \(r_b\) を作成する。これと \(\phi_1, \phi_2\) の組み合わせで境界面を描画する。第4ブロックでは \(\phi_2\) の値を \(\frac{\pi}{12}\) に固定し、 \(\phi_1\) と \(r_b\) のみを動かすことで境界を作成した。同様に、第6ブロックでは \(\phi_2\) の値を \(\frac{\pi}{6}\) に固定して \(\phi_1\) と \(r_b\) のみを動かし、第5・第7ブロックでは \(\phi_1\) の値を \(\frac{\pi}{12}\) または \(\frac{\pi}{6}\) に固定して \(\phi_2\) と \(r_b\) のみを動かした。
線を引く
軸を入れる(基本)
ax.plot([0,3], [0,0], [0,0], color="k")
ax.plot([0,0], [0,3], [0,0], color="k")
ax.plot([0,0], [0,0], [0,3], color="k")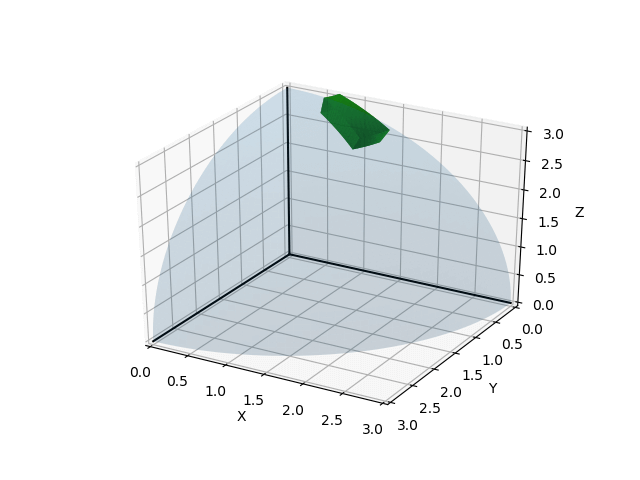
線を引くためにはax.plotを使用する。引数のリストはそれぞれ通る点の \(x,y,z\) 座標を示しており、1行目は点(0,0,0)と(3,0,0)、2行目は点(0,0,0)と(0,3,0)、3行目は点(0,0,0)と(0,0,3)を通る線分を描画している。
任意の線分を引く+透過
ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*1)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*1)*r], [0,np.cos(np.pi/12*1)*r], color="r", alpha=0.5)
ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.cos(np.pi/12*2)*r], color="r", alpha=0.5)
ax.plot([0,np.cos(np.pi/12*2)*np.sin(np.pi/12*1)*r], [0,np.sin(np.pi/12*2)*np.sin(np.pi/12*1)*r], [0,np.cos(np.pi/12*1)*r], color="r")
ax.plot([0,np.cos(np.pi/12*2)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*2)*np.sin(np.pi/12*2)*r], [0,np.cos(np.pi/12*2)*r], color="r")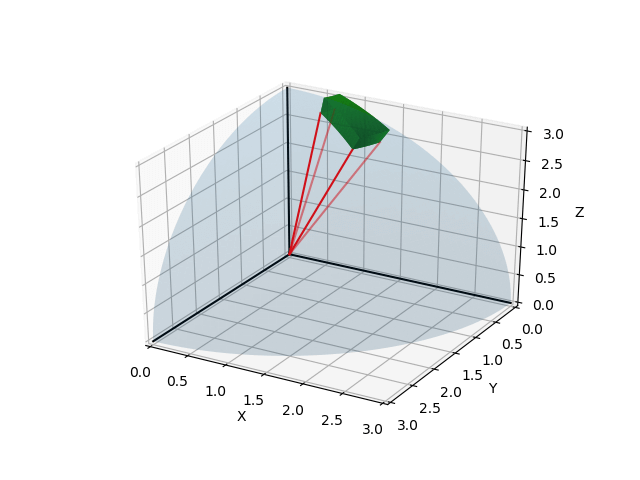
直交座標→極座標変換の関係式を用いて点の \(x,y,z\) 座標をしてやると、原点から先程の領域の線を引くことができる。また、ここでもalpha値を指定してやることで透過効果を加えることができる。
曲線を引く
# ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*1)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*1)*r], [0,np.cos(np.pi/12*1)*r], color="r", alpha=0.5)
# ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.cos(np.pi/12*2)*r], color="r", alpha=0.5)
x_c = np.cos(np.pi/12*2)*np.sin(theta_1_0) * r # xの極座標表示
y_c = np.sin(np.pi/12*2)*np.sin(theta_1_0) * r # yの極座標表示
z_c = np.cos(theta_1_0) * r # zの極座標表示
ax.plot(x_c, y_c, z_c, color="r")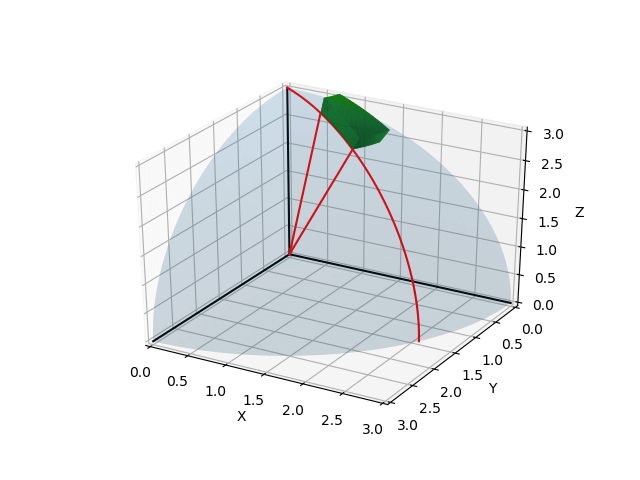
先程描画した線のうち2本を消去し、今度は \(\theta_1\) の回転方向の曲線を描画する。球面や境界を描画するときには変数のうち1つを固定して2つを動かした(配列で指定した) が、線を描画するときにもそれと同じ考えで、変数のうち2つを固定し1つのみを動かす。今回は \(\theta_1\) 方向の回転曲線を描画するため、 \(r\) と \(\theta_2\) を固定し \(\theta_1\) のみを動かして得られた各点の座標を、ax.plotに渡して描画した。
まとめ
以上の技術をすべて合わせると、以下のような作図が可能になる。
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
r = 3 # 半径を指定
theta_1_0 = np.linspace(0, np.pi/2, 100) # θ_1は[0,π/2]の値をとる
theta_2_0 = np.linspace(0, np.pi/2, 100) # θ_2は[0,π/2]の値をとる
theta_1, theta_2 = np.meshgrid(theta_1_0, theta_2_0) # 2次元配列に変換
x = np.cos(theta_2)*np.sin(theta_1) * r # xの極座標表示
y = np.sin(theta_2)*np.sin(theta_1) * r # yの極座標表示
z = np.cos(theta_1) * r # zの極座標表示
phi_1 = np.linspace(np.pi/12*1, np.pi/12*2, 50) # φ_1は[π/12,π/6]の値をとる
phi_2 = np.linspace(np.pi/12*1, np.pi/12*2, 50) # φ_2は[π/12,π/6]の値をとる
phi_1_0, phi_2_0 = np.meshgrid(phi_1, phi_2) # 2次元配列に変換
x_p = np.cos(phi_2_0)*np.sin(phi_1_0) * r # xの極座標表示
y_p = np.sin(phi_2_0)*np.sin(phi_1_0) * r # yの極座標表示
z_p = np.cos(phi_1_0) * r # zの極座標表示
dr = 0.3
x_dp = np.cos(phi_2_0)*np.sin(phi_1_0) * (r + dr) # xの極座標表示
y_dp = np.sin(phi_2_0)*np.sin(phi_1_0) * (r + dr) # yの極座標表示
z_dp = np.cos(phi_1_0) * (r + dr) # zの極座標表示
r_b = np.linspace(r, r+dr, 50) # 半径を[r,r+dr]まで動かす
phi_12_1_1, r_b_12_1_1 = np.meshgrid(phi_1, r_b)
x_12_1_1 = np.cos(np.pi/12*1)*np.sin(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
y_12_1_1 = np.sin(np.pi/12*1)*np.sin(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
z_12_1_1 = np.cos(phi_12_1_1)*r_b_12_1_1 # φ_2をπ/12で固定
phi_12_1_2, r_b_12_1_2 = np.meshgrid(phi_2, r_b)
x_12_1_2 = np.cos(phi_12_1_2)*np.sin(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
y_12_1_2 = np.sin(phi_12_1_2)*np.sin(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
z_12_1_2 = np.cos(np.pi/12*1)*r_b_12_1_2 # φ_1をπ/12で固定
phi_12_2_1, r_b_12_2_1 = np.meshgrid(phi_1, r_b)
x_12_2_1 = np.cos(np.pi/12*2)*np.sin(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
y_12_2_1 = np.sin(np.pi/12*2)*np.sin(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
z_12_2_1 = np.cos(phi_12_2_1)*r_b_12_2_1 # φ_2をπ/6で固定
phi_12_2_2, r_b_12_2_2 = np.meshgrid(phi_2, r_b)
x_12_2_2 = np.cos(phi_12_2_2)*np.sin(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
y_12_2_2 = np.sin(phi_12_2_2)*np.sin(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
z_12_2_2 = np.cos(np.pi/12*2)*r_b_12_2_2 # φ_1をπ/6で固定
x_c = np.cos(theta_2_0)*np.sin(np.pi/12*2) * r # xの極座標表示
y_c = np.sin(theta_2_0)*np.sin(np.pi/12*2) * r # yの極座標表示
z_c = np.cos(np.pi/12*2) * r # zの極座標表示
fig = plt.figure() # 描画領域を作成
ax = fig.add_subplot(111, projection="3d") # 3Dの軸を作成
ax.plot_surface(x,y,z, alpha=0.2) # 球を3次元空間に表示
ax.plot_surface(x_p,y_p,z_p, color="g") # 半径rの球の一部を3次元空間に表示
ax.plot_surface(x_dp,y_dp,z_dp, color="g") # 半径r+drの球の一部を3次元空間に表示
ax.plot_surface(x_12_1_1,y_12_1_1,z_12_1_1, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_1_2,y_12_1_2,z_12_1_2, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_2_1,y_12_2_1,z_12_2_1, color="g") # 境界を3次元空間に表示
ax.plot_surface(x_12_2_2,y_12_2_2,z_12_2_2, color="g") # 境界を3次元空間に表示
ax.plot([0,3], [0,0], [0,0], color="k")
ax.plot([0,0], [0,3], [0,0], color="k")
ax.plot([0,0], [0,0], [0,3], color="k")
ax.plot([0,np.cos(np.pi/12*2)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*2)*np.sin(np.pi/12*2)*r], [0,np.cos(np.pi/12*2)*r], color="r")
ax.plot([0,np.cos(np.pi/12*2)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*2)*np.sin(np.pi/12*2)*r], [np.cos(np.pi/12*2)*r,np.cos(np.pi/12*2)*r], color="b")
ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.cos(np.pi/12*2)*r], color="r", alpha=0.5)
ax.plot([0,np.cos(np.pi/12*1)*np.sin(np.pi/12*2)*r], [0,np.sin(np.pi/12*1)*np.sin(np.pi/12*2)*r], [np.cos(np.pi/12*2)*r,np.cos(np.pi/12*2)*r], color="b", alpha=0.5)
ax.plot(x_c, y_c, z_c, color="b")
plt.xlim([0,3])
plt.ylim([3,0]) # Y軸の表示は初期値とは逆にする
ax.set_zlim([0,3])
plt.xlabel("X")
plt.ylabel("Y")
ax.set_zlabel("Z")
plt.show()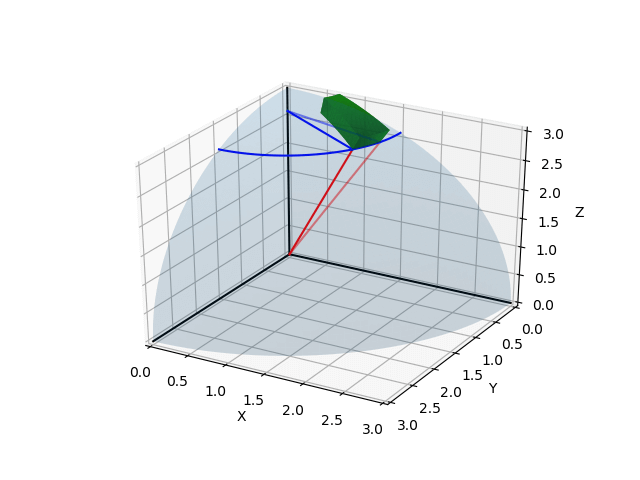

Comments