$$\newcommand{\bra}[1]{\left\langle #1 \right|}$$
$$\newcommand{\ket}[1]{\left|#1 \right\rangle}$$
量子力学における密度行列は、量子状態を表現した演算子です。
その要素には、基底ベクトルに基づいた添字を割り振ることができ、そこから部分転置を計算することができます。
この記事では、密度行列と部分転置について解説し、部分転置をブロック行列の転置として解釈することで、Pythonによる実装を可能にします。
密度行列
定義
それぞれの基底が
$$\left\{\ket{e_k^{(1)}}\right\},\quad\left\{\ket{e_k^{(2)}}\right\}$$
で与えられる2成分形の量子状態を密度行列 \(\rho\) であらわします。
なお、密度行列の要素は、それぞれの基底の添え字をもちいて \(\rho_{ij,kl}\) と書け、
$$\rho_{ij,kl}=\left(\bra{e_i^{(1)}}\otimes\bra{e_j^{(2)}}\right)\rho\left(\ket{e_k^{(1)}}\otimes\ket{e_l^{(2)}}\right)\tag{1}$$
という計算で抽出することができます。
解説
式 \((1)\) について、図式的に解説します。
$$\rho=\begin{pmatrix}a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p\end{pmatrix}$$
という密度行列があるとして、これを構成する基底ベクトルが
- \(\ket{e_1^{(1)}}=\begin{pmatrix}1 \\ 0 \end{pmatrix}\)
- \(\ket{e_2^{(1)}}=\begin{pmatrix}0 \\ 1 \end{pmatrix}\)
- \(\ket{e_1^{(2)}}=\begin{pmatrix}1 \\ 0 \end{pmatrix}\)
- \(\ket{e_2^{(2)}}=\begin{pmatrix}0 \\ 1 \end{pmatrix}\)
であるとします。
要素の抽出のために、
- 第1成分の第1基底と第2成分の第1基底のテンソル積
- 第1成分の第1基底と第2成分の第2基底のテンソル積
の2つを用いた場合、この要素は \(\rho_{11,12}\) と書け、
$$\rho_{11,12}=\left(\bra{e_1^{(1)}}\otimes\bra{e_1^{(2)}}\right)\begin{pmatrix}a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p\end{pmatrix}\left(\ket{e_1^{(1)}}\otimes\ket{e_2^{(2)}}\right)$$
$$=(\begin{pmatrix}1 & 0 \end{pmatrix}\otimes\begin{pmatrix}1 & 0 \end{pmatrix})\begin{pmatrix}a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p\end{pmatrix}\left(\begin{pmatrix}1 \\ 0 \end{pmatrix}\otimes\begin{pmatrix}0 \\ 1 \end{pmatrix}\right)$$
$$=\begin{pmatrix}1 & 0 & 0 & 0 \end{pmatrix}\begin{pmatrix}a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p\end{pmatrix}\begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}$$
$$=\begin{pmatrix}a & b & c & d \end{pmatrix}\begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \end{pmatrix}$$
$$=b$$
より、密度行列 \(\rho\) の要素 \(b\) に対応することがわかります。
同様の計算を繰り返すと、 \(\rho\) の各成分は以下のように書けます。
$$\rho=\begin{pmatrix}\rho_{11,11} & \rho_{11,12} & \rho_{11,21} & \rho_{11,22} \\ \rho_{12,11} & \rho_{12,12} & \rho_{12,21} & \rho_{12,22} \\ \rho_{21,11} & \rho_{21,12} & \rho_{21,21} & \rho_{21,22} \\ \rho_{22,11} & \rho_{22,12} & \rho_{22,21} & \rho_{22,22}\end{pmatrix}$$
部分転置
定義
密度行列 \(\rho\) の各要素について、2番目の添え字を入れ替え、
$$\rho_{ij,kl}\to\rho_{il,kj}$$
という操作を行った行列を、部分転置行列 \(\rho^{pt}\) と定義します。
部分転置の例
2基底×2基底
先ほどの密度行列 \(\rho\) の部分転置 \(\rho^{pt}\) の各成分は、
$$\rho^{pt}=\begin{pmatrix}\rho^{pt}_{11,11} & \rho^{pt}_{11,12} & \rho^{pt}_{11,21} & \rho^{pt}_{11,22} \\ \rho^{pt}_{12,11} & \rho^{pt}_{12,12} & \rho^{pt}_{12,21} & \rho^{pt}_{12,22} \\ \rho^{pt}_{21,11} & \rho^{pt}_{21,12} & \rho^{pt}_{21,21} & \rho^{pt}_{21,22} \\ \rho^{pt}_{22,11} & \rho^{pt}_{22,12} & \rho^{pt}_{22,21} & \rho^{pt}_{22,22}\end{pmatrix}$$
と書けます。
3基底×2基底
第2成分の基底は先ほどの2つのままで、第1成分の基底が
- \(\ket{e_1^{(1)}}=\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\)
- \(\ket{e_2^{(1)}}=\begin{pmatrix}0 \\ 1 \\ 0 \end{pmatrix}\)
- \(\ket{e_3^{(1)}}=\begin{pmatrix}0 \\ 0 \\ 1 \end{pmatrix}\)
の3つある場合を考えます。
このとき、3基底×2基底=6より、密度行列は6×6行列となります。
この時の密度行列 \(\rho\) を
$$\rho=\begin{pmatrix}a & b & c & d & e & f \\ g & h & i & j & k & l \\ m & n & o & p & q & r \\ s & t & u & v & w & x \\ y & z & \alpha & \beta & \gamma & \delta \\ \epsilon & \zeta & \eta & \theta & \iota & \kappa\end{pmatrix}$$
とおきます。
部分転置をとった結果のみを示すと、以下のようになります。
(各要素を取り出すための計算に基づいて要素 \(\rho_{ij,kl}\) の添字を決定することで確認できる)
$$\rho^{pt}=\begin{pmatrix}a & g & c & i & e & k \\ b & h & d & j & f & l \\ m & s & o & u & q & w \\ n & t & p & v & r & x \\ y & \epsilon & \alpha & \eta & \gamma & \iota \\ z & \zeta & \beta & \theta & \delta & \kappa\end{pmatrix}$$
以上のような行列の変換には、どのような法則があるでしょうか?
それを示すために、以下のように補助線を入れてみます。
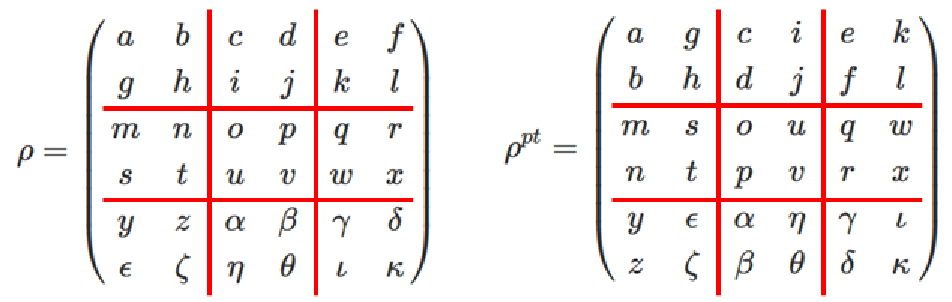
すると、部分転置とは、これらの補助線で区切られたブロック内の行列をそれぞれ転置したものであることがわかります。
すなわち、第1成分の基底の個数を \(N_1\) 、第2成分の基底の個数を \(N_2\) とすると、
密度行列を \(N_1\times N_1\) のブロック行列と見て、
各ブロックを構成する \(N_2\times N_2\) 行列をそれぞれ転置することで部分転置が得られます。
部分転置の実装
以上の処理は、次のようなPythonコードによって実装できます。
partial_transposition関数に密度行列
$$\rho=\begin{pmatrix}10 & 11 & 12 & 13 & 14 & 15 \\ 16 & 17 & 18 & 19 & 20 & 21 \\ 22 & 23 & 24 & 25 & 26 & 27 \\ 28 & 29 & 30 & 31 & 32 & 33 \\ 34 & 35 & 36 & 37 & 38 & 39 \\ 40 & 41 & 42 & 43 & 44 & 45\end{pmatrix}$$
を入力すると、部分転置
$$\rho^{pt}=\begin{pmatrix}10 & 16 & 12 & 18 & 14 & 20 \\ 11 & 17 & 13 & 19 & 15 & 21 \\ 22 & 28 & 24 & 30 & 26 & 32 \\ 23 & 29 & 25 & 31 & 27 & 33 \\ 34 & 40 & 36 & 42 & 38 & 44 \\ 35 & 41 & 37 & 43 & 39 & 45\end{pmatrix}$$
を出力します。
参考文献
- 中原幹夫「量子物理学のための線形代数 =ベクトルから量子情報へ」(2016)培風館.


Comments