概要
実は一般にこれ成り立ちます https://t.co/g5PjQKh9Qi pic.twitter.com/xpSUrF0cFX
— ハクリュー (@hakuryu27071454) February 27, 2023
こちらのツイートを拝見し、自力で証明してみたくなったので、その結果を記録した。本当は式変形から \(\phi=3\theta\) の形を導きたかったが、今回は \(\phi=3\theta\) のときに力学的条件式をみたし、 \(\phi\) と \(\theta\) が1対1対応であることから結果を確認した。
問題設定
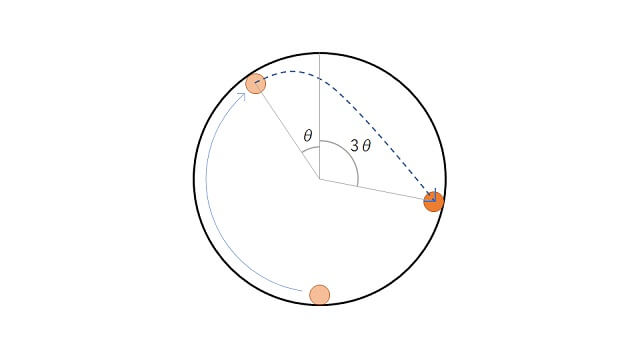
重力方向に対し垂直に立てた円形の枠を考える。
枠の最下点から球を打ち出すと、最上点に到達する前に球は枠から離れ、放物線を描いて枠のある点に落下した。
このとき、球が枠から離れた点と枠の中心を結ぶ線分と、枠の最上・最下点を結ぶ線分が成す角を \(\theta \left(0<\theta<\frac{\pi}{2}\right)\) 、同様に、球が枠に落下した点と枠の中心を結ぶ線分と、枠の最上・最下点を結ぶ線分が成す角を \(\phi\) とする。
この設定において、
$$\phi=3\theta$$
が成り立つことを証明せよ。
証明
変数の定義
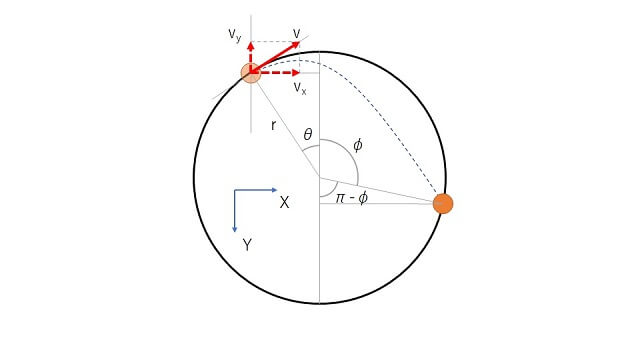
X軸を向かって右方向が正、Y軸を重力方向が正となるようにとる。球が枠から離れた時の速度を \(v\) 、枠の半径を \(r\) 、重力加速度を \(g\) とする。
証明に用いる関係式
三平方の定理や加法定理
$$\sin(a\pm b)=\sin a\cos b\pm\cos a\sin b$$
$$\cos(a\pm b)=\cos a\cos b\mp\sin a\sin b$$
を用いて、以下の移動の公式や三倍角の公式を導いておく。
$$\sin(\pi-\phi)=\sin\phi\tag{1}$$
$$\cos(\pi-\phi)=-\cos\phi\tag{2}$$
$$\sin 3\theta=3\sin\theta\cos^2\theta-\sin^3\theta\tag{3}$$
$$\cos 3\theta=\cos^3\theta-3\sin^2\theta\cos\theta\tag{4}$$
また、以下の関係式が成り立つ。
$$\cos^4\theta-\sin^4\theta=(\cos^2\theta)^2-\sin^4\theta$$
$$=(1-\sin^2\theta)^2-\sin^4\theta$$
$$=1-2\sin^2\theta+\sin^4\theta-\sin^4\theta$$
$$=1-2\sin^2\theta\tag{5}$$
最後に、以下の等加速度直線運動の公式を用いる。
$$x=v_0t+\frac{1}{2}at^2\tag{6}$$
放物運動としての立式

\(v\) のX, Y軸成分をそれぞれ \(v_x, v_y\) とすると
$$v_x=v\cos\theta$$
$$v_y=-v\sin\theta$$
である。
球が枠から離れて落下するまでの時間を \(t\) とすると、この間にX軸方向には
$$r\sin\theta+r\sin(\pi-\phi)=r(\sin\theta+\sin(\pi-\phi))$$
$$=r(\sin\theta+\sin\phi)\quad(\because{(1)})$$
だけ移動している。この移動は等速直線運動であるので、
$$r(\sin\theta+\sin\phi)=v_xt$$
$$r(\sin\theta+\sin\phi)=v\cos\theta\cdot t$$
これを \(t\) について解くと
$$t=\frac{r}{v}\frac{\sin\theta+\sin\phi}{\cos\theta}\tag{7}$$
となる。
Y軸方向には
$$r\cos\theta+r\cos(\pi-\phi)=r(\cos\theta+\cos(\pi-\phi))$$
$$=r(\cos\theta-\cos\phi)\quad(\because{(2)})$$
だけ移動する。この運動は等加速度直線運動より、関係式 \((6)\) を用いると
$$r(\cos\theta-\cos\phi)=v_yt+\frac{1}{2}gt^2$$
$$r(\cos\theta-\cos\phi)=-v\sin\theta\cdot t+\frac{1}{2}gt^2$$
となる。 \((7)\) 式を代入して \(t\) を消去すると
$$r(\cos\theta-\cos\phi)=-\frac{rv}{v}\frac{\sin\theta(\sin\theta+\sin\phi)}{\cos\theta}+\frac{1}{2}\frac{gr^2}{v^2}\frac{(\sin\theta+\sin\phi)^2}{\cos^2\theta}$$
$$\cos\theta-\cos\phi=-\frac{\sin\theta(\sin\theta+\sin\phi)}{\cos\theta}+\frac{1}{2}\frac{gr}{v^2}\frac{(\sin\theta+\sin\phi)^2}{\cos^2\theta}\tag{8}$$
円運動としての立式
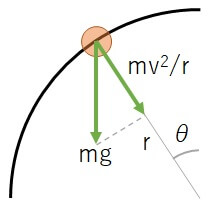
球の質量を \(m\) とする。
球が枠から離れた点において、球は円運動をしているため、球には向心力 \(m\frac{v^2}{r}\) が働いている。
また、この点において、球が枠から受ける垂直抗力は \(0\) とみなすことができるため、この向心力は球にかかる重力の分解成分によってのみ生じる。
したがって
$$mg\cos\theta=m\frac{v^2}{r}$$
$$\frac{gr}{v^2}=\frac{1}{\cos\theta}\tag{9}$$
が成り立つ。
式の整理
\((9)\) 式を \((8)\) 式に代入し、 \(\phi\) を含む項を右辺に集める。
$$\cos\theta-\cos\phi=-\frac{\sin\theta(\sin\theta+\sin\phi)}{\cos\theta}+\frac{1}{2}\frac{(\sin\theta+\sin\phi)^2}{\cos^3\theta}$$
$$2\cos^3\theta(\cos\theta-\cos\phi)=-2\sin\theta\cos^2\theta(\sin\theta+\sin\phi)+(\sin\theta+\sin\phi)^2$$
$$2\cos^4\theta-2\cos^3\theta\cos\phi=-2\sin^2\theta\cos^2\theta-2\sin\theta\cos^2\theta\sin\phi+\sin^2\theta+2\sin\theta\sin\phi+\sin^2\phi$$
$$2\cos^4\theta+2\sin^2\theta\cos^2\theta-\sin^2\theta=2\cos^3\theta\cos\phi+2\sin\theta\sin\phi(1-\cos^2\theta)+\sin^2\phi$$
$$2\cos^4\theta+2\sin^2\theta\cos^2\theta-\sin^2\theta=2\cos^3\theta\cos\phi+2\sin^3\theta\sin\phi+\sin^2\phi\tag{10}$$
左辺の評価
左辺を変形すると
$$(左辺)=2\cos^2\theta(\cos^2\theta+\sin^2\theta)-\sin^2\theta$$
$$=2\cos^2\theta-\sin^2\theta$$
$$=2\cos^2\theta-(1-\cos^2\theta)$$
$$=3\cos^2\theta-1$$
となる。
右辺の評価
\(\phi=3\theta\) とおいて右辺を計算すると
$$(右辺)=2\cos^3\theta\cos 3\theta+2\sin^3\theta\sin 3\theta+\sin^2 3\theta$$
$$=2\cos^3\theta(\cos^3\theta-3\sin^2\theta\cos\theta)+2\sin^3\theta(3\sin\theta\cos^2\theta-\sin^3\theta)+(3\sin\theta\cos^2\theta-\sin^3\theta)^2\quad(\because(3, 4))$$
$$=2\cos^6\theta-6\sin^2\theta\cos^4\theta+6\sin^4\theta\cos^2\theta-2\sin^6\theta+9\sin^2\theta\cos^4\theta-6\sin^4\theta\cos^2\theta+\sin^6\theta$$
$$=2\cos^6\theta+3\sin^2\theta\cos^4\theta-\sin^6\theta$$
$$=2\cos^4\theta(\cos^2\theta+\sin^2\theta)+\sin^2\theta(\cos^4\theta-\sin^4\theta)$$
$$=2\cos^4\theta+\sin^2\theta(1-2\sin^2\theta)\quad(\because(5))$$
$$=2\cos^4\theta+\sin^2\theta-2\sin^4\theta$$
$$=2(\cos^4\theta-\sin^4\theta)+\sin^2\theta$$
$$=2(1-2\sin^2\theta)+\sin^2\theta\quad(\because(5))$$
$$=2-3\sin^2\theta$$
$$=2-3(1-\cos^2\theta)$$
$$=3\cos^2\theta-1$$
以上より、 \(\phi=3\theta\) のとき、 \((10)\) 式が成立することが示された。
結論
また、球が枠から離れる地点( \(\theta\) )が決まれば、球が落下する地点( \(\phi\) )は一意に定まるので、この問題設定では \(\phi=3\theta\) となることが示された。

Comments