この記事について
- C++やPythonが大半を占める神経回路シミュレーションの世界で、Rustを使ってみようって話です。
- この記事は神経科学 Advent Calenderの2019年12月11日分です。
- 同様の内容をRust LT #7でLTしましたが、この記事はもっとRust初心者向けです。
「並列化はいいぞ」と何度も叫びますが、サンプルコードは並列化されていません。許して。- 皆さんのお力添えのおかげで、現在はrayonで並列化されています。
- 最新のコードはgithubをご覧ください。
LT資料
[slideshare id=204395292&doc=lt20191211-191211110706]
Rust LT #7でLTした似た内容のスライドです。
北陸新幹線の中で超特急でつくったため、たぶん、何が言いたいか全くわからないと思います。
Rustとは?
- プログラミング言語です。
- Cと同じくらい早いです。
- バグりやすい処理を、あらかじめコンパイラがダメ出ししてくれます。
- そのため、非常に安全です。
- ゆえに、並列化しても安全性が高いです。
なぜRustで神経回路シミュレーションをするか?
現在の神経回路シミュレーション界隈は、C++とPythonが主流で、そこにJuliaが挑戦している感じです(弊社調べ)。
しかし、大規模な神経回路をシミュレートする際にはPythonだと非常に遅い。数万の神経細胞を1ステップ10μsecで30分走らせるとなると絶望です。
C++はすぐバグる。配列の外を参照して、か弱い神経細胞に数億Aの電流が流れるということが良く起こる。神経回路の中で何が起こるかわからないからシミュレーションしてるのに、その最中にヤバいことが起こっても気付けるわけがない。
Juliaはなんか嫌。初速が遅い気がする(気のせい?)。
その点、Rustなら安心。Cと同程度の速度が出るし、安全性が保障されている。
「安全性が保障されている」とはどういうことか?これは、Rustのコンパイラが徹底的にバグの温床を潰しにくるということです。関数がとある値を利用している状況で、他の関数がそれを変更しにくると当然のように止める。さらに、実際には変更せずとも、変更しうる状況になったら辞めさせる。なんなら、変数名のつけ方にまで文句を言う。つまり、コンパイルはなかなか通らないが、通りさえすればバグらないことが保障されるのです。
そして、処理を並列化した際にも安全性は保障されます。同時に走っているニューロンがブッキングするようなこともありません。
とりあえず書いてみる
個々の神経のモデルにはIntegrate-and-Fireモデルライクなものを用います。
このへんの関係式は適当に設計したので、適宜変更してください。
struct Neuron {
synapses: Vec<usize>,
weights: Vec<f64>,
v: f64,
i_ext: f64,
threshold: f64,
t_rest: f64,
}というわけで、個々のニューロンをstructを使って実装しましょう。1個のニューロンは、それが刺激を受け取るニューロンのIDと結合強度が格納された配列(synapsesとweights)、膜電位v、外部電流i_ext、閾値threshold、不応期を計測する変数t_restを持ちます。
impl Neuron {
fn new(n: usize) -> Neuron {
let mut synapses: Vec<usize> = Vec::new();
let mut weights: Vec<f64> = Vec::new();
for i in 0..n {
if random::<f64>() < 0.5 {
synapses.push(i);
weights.push(random::<f64>() * 10.0);
}
}
Neuron {
synapses: synapses,
weights: weights,
v: 0.0,
i_ext: 0.0,
threshold: 10.0,
t_rest: 0.0,
}
}
fn run(&mut self, spike: &Vec<u8>, dt: f64) -> u8 {
if self.t_rest > 0.0 {
self.t_rest -= dt;
if self.t_rest <= 0.0 {
self.v = 0.0;
}
1
} else {
let mut i_rec = 0.0;
for i in 0..self.synapses.len() {
if spike[self.synapses[i]] == 1 {
i_rec += self.weights[i];
}
}
let i_ext = self.i_ext * (1.0 + self.i_ext * random::<f64>());
let d_v = |y: f64| (-y + 1.0 * (i_rec + i_ext)) / 50.0;
self.v += rk4(d_v, self.v, dt);
if self.v > self.threshold {
self.t_rest = 2.0;
1
} else {
0
}
}
}
}implを用いることで、このstructにメンバー関数やメソッドを追加することができます。
関数newではニューロンを新設する方法を設定しましょう。ここでは、一定確率で他のニューロン(自分自身を含む)とシナプスを形成し、その重みは0.0から10.0の範囲を取ることにしています。
メソッドrunでは微分方程式を処理し、閾値を超えたら1(スパイク)、そうでなければ0を返します。メソッドを書く際には、引数の先頭に&mut selfを置くことを忘れないようにしましょう。
fn rk4<F: Fn(f64) -> f64>(f: F, y: f64, h: f64) -> f64 {
let k1 = h * f(y);
let k2 = h * f(y + 0.5 * k1);
let k3 = h * f(y + 0.5 * k2);
let k4 = h * f(y + k3);
(k1 + 2.0 * k2 + 2.0 * k3 + k4) / 6.0
}rk4はルンゲクッタ法を実装した関数です。
struct Network {
n: usize,
neurons: Vec<Neuron>,
count: usize,
}
impl Network {
fn new(n: usize) -> Network {
let mut neurons: Vec<Neuron> = Vec::with_capacity(n);
for _ in 0..n {
neurons.push(Neuron::new(n));
}
Network {
n: n,
neurons: neurons,
count: 0,
}
}
fn run(&mut self, spike_train: &Vec<Vec<u8>>, dt: f64) -> Vec<u8> {
let mut spike: Vec<u8> = vec![0; self.n];
for i in 0..self.n {
spike[i] = self.neurons[i].run(&spike_train[self.count], dt);
}
self.count += 1;
spike
}
fn input(&mut self, current: f64) {
for i in 0..self.n {
self.neurons[i].i_ext = current;
}
}
}これは個人的な感想ですが、マルチエージェントなシミュレーションにおいては、すべてのエージェントを統括するような存在がいると便利な気がします。というわけでNeuronを統括するNetworkを構築します。
Networkはフィールドにニューロン数nを持ち、n個のNeuronをneuronsに収納します。また、独自にステップ数を数える変数countを使用します。
メソッドrunではn個のニューロンに1ステップ前の神経活動情報を与え、すべてのニューロン活動を検証します。本来は、ここで並列化が効果を発揮するでしょう。inputでは、すべてのニューロンに与えられる外部電流の大きさを変更します。
fn main() {
const N: usize = 100;
let mut spike_train: Vec<Vec<u8>> = vec![Vec::new()];
for _ in 0..N {
if random::<f64>() < 0.5 {
spike_train[0].push(1);
} else {
spike_train[0].push(0);
}
}
let mut network: Network = Network::new(N);
let mut t = 0.0;
let dt = 0.1;
let mut x: Vec<f64> = Vec::new();
let mut y: Vec<f64> = Vec::new();
// y.push(0.0);
while t <= 4000.0 { // 800.0
if (t >= 1000.0) & (t <= 3000.0) { // 200, 600
network.input(5.0);
} else {
network.input(4.0);
}
spike_train.push(network.run(&spike_train, dt));
t += dt;
// x.push(t);
// y.push(network.neurons[0].v);
println!("{}", t);
}
let time_all = spike_train.len();
for i in 0..time_all {
for j in 0..N {
if spike_train[i][j] == 1 {
x.push(i as f64 * dt);
y.push(j as f64);
}
}
}
let mut y: Vec<f64> = Vec::with_capacity(spike_train.len());
for i in 0..spike_train.len() {
y.push(spike_train[i][0] as f64)
}
let mut fg = gnuplot::Figure::new();
fg.axes2d()
.lines(x.iter(), y.iter(), &[gnuplot::Color("blue")])
//.lines(x.iter(), y.iter(), &[gnuplot::Color("blue")])
.set_x_range(Fix(0.0), Fix(4000.0));
fg.echo_to_file("spike_train.plt"); // voltage.plt
}実験操作はmain関数に記述します。ここでは、dt=0.1でt=4000.0だけシミュレーションを行い、そのうち\(1000.0\leq t \leq 3000.0\)の時間帯は外部電流を増強します。
spike_trainが神経活動を記録する配列で、最終的な図表の作成とニューロンに与える入力を保存するために使用します。すなわち、
- Networkがspike_trainをNeuronに読ませる
- Neuronが0or1を返す
- Networkが各Neuronの返り値をspike_trainに渡す
- さっきの値をNetworkがNeuronに読ませる
- …
という流れを取ります。
全ソースコードはこちら
成果物
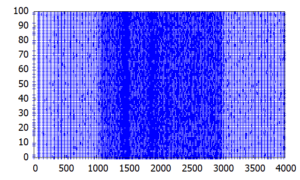
x軸が時間、y軸がニューロンのID、青い点が神経活動を表します。外部電流が小さかった時にはまばらだった活動が、外部電流を上げることで高頻度のバーストに変化していることがわかります。
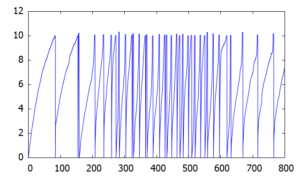
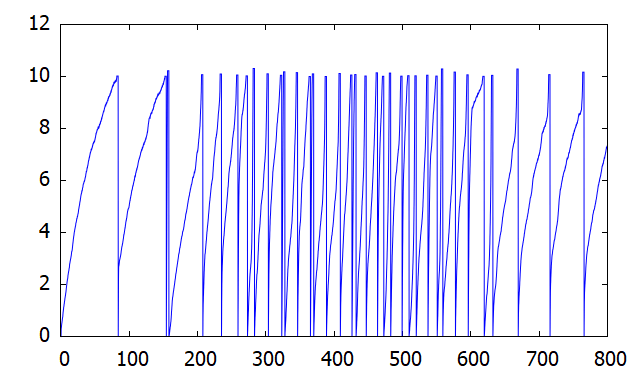
ちなみに、個々のニューロンの膜電位は上図のように変化します。(\(200.0\geq t\geq 600.0\)の期間に外部電流を増強)
並列化するなら
今回はすべてのニューロンを直列で計算しましたが、Rustのメリットを活かすなら、これらの計算を並列化することが効果的です。並列化の手法としては、ニューロンを何分の1かずつに分割し、複数のスレッドで処理を行って最後に合わせるフォーク・ジョイン並列などが有名ですが、ここでは神経回路特有の工夫点について説明します。
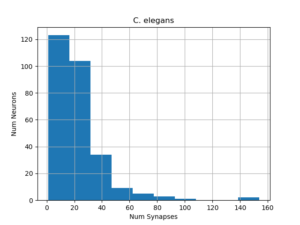
この図はC. elegans(線虫)の全神経細胞を、それぞれが入力を受け取る他の神経細胞の数ごとに集計したものです。この図によると、ほとんどのニューロンは少ないニューロンとしか接続していませんが、一方で、非常に多くのニューロンと接続したニューロンがわずかに存在します。この分布は、y軸を適当に対数変換すると直線系になり、べき乗則というルールにしたがいます。つまり、「ほとんどは『持たざる者』だが、ごく少数の者は大量に持っている」というルールです。
このような状況下では、各ニューロンごとに仕事量が大きく異なるため、均等な割り付けをランダムに行うだけではあまり高速化できません。そのため、シナプス数などのパラメータを参考に、割り付けを工夫する必要があります。
このような現象は、神経回路のみならず、ネットワーク構造をとるものにおいて一般的に見られるものです。
結論
Rustはいいぞ。
Rustは高速で安全で並列化できていいぞ。
みんなで神経回路シミュレーションの共通言語をRustにしよう。
※Rustのインストール方法や基本文法については、各種Webページや書籍を参考にしてください。
※Rustのプロの方は、Rust的な書き方についてアドバイスをいただけると幸いです。

Comments