 How to Solve Differential Equation
How to Solve Differential Equation【微分方程式の解法2】1階同次形
1階同次形と呼ばれる微分方程式の解き方について解説する。登場する変数の次数が等しいため、それらを分数の形にして新たな変数へと変換し、変数分離型へ帰着させることを基本方針とする。その際、分母になる変数が0となる場合を考慮し、場合分けして計算するよう注意する。
 How to Solve Differential Equation
How to Solve Differential Equation How to Solve Differential Equation
How to Solve Differential Equation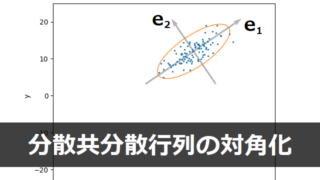 Probability and Statistics
Probability and Statistics How to Solve Differential Equation
How to Solve Differential Equation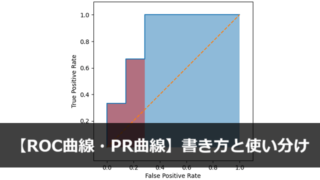 Machine Learning and AI
Machine Learning and AI How to Solve Differential Equation
How to Solve Differential Equation Machine Learning and AI
Machine Learning and AI Matplotlib
Matplotlib Mathematics
Mathematics