概要
この記事では、分散共分散行列が対角行列となるように変数変換を行う方法、もしくは分散の方向が独立となるような軸の見つけ方について解説し、その導出を行う。
これは、主成分分析(Principal Component Analysis; PCA)の原理として考えることができる。
分散共分散行列の対角化
問題設定
(x, y) の2次元における分散共分散行列が
$$boldsymbol{Sigma}=begin{pmatrix}
sigmax^2 & sigma{xy} \
sigma_{xy} & sigma_y^2
end{pmatrix}$$
であるとき、 (u=u(x,y), v=v(v,y)) という変数変換を適切に行うと、2変数 (u,v) の分散共分散行列を
$$boldsymbol{Sigma}'=begin{pmatrix}
sigma_u^2 & 0 \
0 & sigma_v^2
end{pmatrix}$$
の形で表すことができる。このとき、 (u=u(x,y), v=v(v,y)) の変換と (boldsymbol{Sigma}') を求める。
問題の再設定
(u=u(x,y), v=v(v,y)) の変換を求めるためには少々複雑な計算が必要となるので、問題を以下のように言い換える(余力があれば、本記事の読了後に導出してみるとよい)。
(u,v) についての任意のベクトル (boldsymbol{nu}') は、直交基底
$$mathbf{e}_u'=begin{pmatrix} 1 \ 0 end{pmatrix}, mathbf{e}_v'=begin{pmatrix} 0 \ 1 end{pmatrix}$$
を用いて (boldsymbol{nu}=amathbf{e}_u'+bmathbf{e}_v') と書ける。 (boldsymbol{Sigma}') との積をとると
$$boldsymbol{Sigma}'boldsymbol{nu}'=boldsymbol{Sigma}'(amathbf{e}_u'+bmathbf{e}_v')$$
$$=asigma_u^2mathbf{e}_u'+bsigma_v^2mathbf{e}_v'$$
と簡単に計算できるが、これは (boldsymbol{Sigma}') の共分散の項が0であり、 (u,v) を独立に計算できるためである。
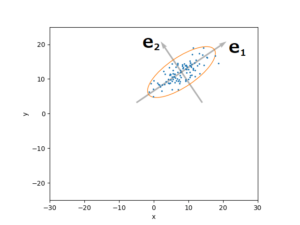
ここで (x,y) についても直交基底 (mathbf{e}_1, mathbf{e}_2) をうまくとることで、任意のベクトル (boldsymbol{nu}) を (boldsymbol{nu}=amathbf{e}_1+bmathbf{e}_2) と書くことができ、 (boldsymbol{Sigma}) との積に関して
$$boldsymbol{Sigma}boldsymbol{nu}=boldsymbol{Sigma}(amathbf{e}_1+bmathbf{e}_2)$$
$$=asigma_u^2mathbf{e}_1+bsigma_v^2mathbf{e}_2tag{1}$$
が成り立つとする。このとき、 (mathbf{e}_1, mathbf{e}_2) のベクトルと (boldsymbol{Sigma}') を求める。
定理
(sigma_u^2geqsigma_v^2) とすると、各変数は以下のように求められる。
$$sigma_u^2=frac{(sigma_x^2+sigma_y^2)+sqrt{(sigma_x^2-sigmay^2)^2+4sigma{xy}^2}}{2}$$
$$sigma_v^2=frac{(sigma_x^2+sigma_y^2)-sqrt{(sigma_x^2-sigmay^2)^2+4sigma{xy}^2}}{2}$$
$$mathbf{e}_1=left(1,frac{sigma_u^2-sigmax^2}{sigma{xy}}right)$$
$$mathbf{e}_2=left(1,frac{sigma_v^2-sigmax^2}{sigma{xy}}right)$$
証明
((1)) 式における (alphamathbf{e}=boldsymbol{Sigma}mathbf{e}) のような関係をみたすのは、 (alpha) と (mathbf{e}) が、それぞれ (boldsymbol{Sigma}) の固有値と固有ベクトルとなるときである。 (mathbf{e}=(e_x,e_y)) とおいて成分を書き下すと
$$alphabegin{pmatrix} e_x \ e_y end{pmatrix}=begin{pmatrix} sigmax^2 & sigma{xy} \ sigma_{xy} & sigma_y^2 end{pmatrix}begin{pmatrix} e_x \ e_y end{pmatrix}$$
$$begin{pmatrix} alpha e_x \ alpha e_y end{pmatrix}=begin{pmatrix} sigma_x^2 ex+sigma{xy}ey \ sigma{xy}e_x+sigma_y^2 e_y end{pmatrix}$$
より、成分どうしを比較して
$$begin{eqnarray}left{begin{array}{l} alpha e_x=sigma_x^2 ex+sigma{xy}e_yquad(2) \ alpha ey=sigma{xy}e_x+sigma_y^2 e_y quad(3)end{array}right.end{eqnarray}$$
((2)) 式より
$$e_y=frac{alpha-sigmax^2}{sigma{xy}}e_xtag{4}$$
((3)) 式に代入して
$$alphafrac{alpha-sigmax^2}{sigma{xy}}ex=sigma{xy}e_x+sigma_y^2frac{alpha-sigmax^2}{sigma{xy}}e_x$$
$$alpha(alpha-sigmax^2)=sigma{xy}^2+sigma_y^2(alpha-sigma_x^2)$$
$$alpha^2-(sigma_x^2+sigma_y^2)alpha+(sigma_x^2sigmay^2-sigma{xy}^2)=0$$
解の公式より
$$alpha=frac{(sigma_x^2+sigma_y^2)pmsqrt{(sigma_x^2+sigma_y^2)^2-4(sigma_x^2sigmay^2-sigma{xy}^2)}}{2}$$
$$alpha=frac{(sigma_x^2+sigma_y^2)pmsqrt{(sigma_x^2-sigmay^2)^2+4sigma{xy}^2}}{2}$$
(sigma_u^2geqsigma_v^2) とすると、大小の固有値をそれぞれに割り当てて
$$sigma_u^2=frac{(sigma_x^2+sigma_y^2)+sqrt{(sigma_x^2-sigmay^2)^2+4sigma{xy}^2}}{2}$$
$$sigma_v^2=frac{(sigma_x^2+sigma_y^2)-sqrt{(sigma_x^2-sigmay^2)^2+4sigma{xy}^2}}{2}$$
となる。また、 ((4)) 式の関係より、対応する固有ベクトルは
$$mathbf{e}_1=left(1,frac{sigma_u^2-sigmax^2}{sigma{xy}}right)$$
$$mathbf{e}_2=left(1,frac{sigma_v^2-sigmax^2}{sigma{xy}}right)$$
と書ける。
なお、導出に際して、 (sigma_{xy}neq 0, e_xneq 0) であることを仮定した。

Comments