What is the logistic equation?
The logistic equation is an ordinary differential equation given by
$$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)\tag{1}$$
where
- \(N\) : Population of organisms
- \(t\) : Time
- \(r\) : Intrinsic growth rate
- Maximum potential rate of increase in reproduction that the target organism has.
- \(K\) : Carrying capacity
- Maximum number of organisms that can exist in the environment.
This equation represents the change in the population of an organism over time.
Derivation of the logistic equation
Malthusian model
The predecessor to the logistic equation is the Malthusian model:
$$\frac{dN}{dt}=mN\tag{2}$$
This equation expresses that the increase in the number of organisms is proportional to the number of parental generations (= individuals present now; each parent produces \(m\) offspring), which when solved yields
$$N=\exp{(mt)}+C$$
where \(C\) is a constant which depends on the initial value. It shows that the population continues to increase literally exponentially. The model is based on Thomas Robert Malthus' statement in "An Essay on the Principle of Population" that population increased geometrically. \(m\) is called the Malthus' coefficient.
Logistic equation
However, as in the model above, it is unlikely that the number of individuals will continue to rise indefinitely. The carrying capacity, \(K\), was introduced based on the idea that there should approximately be an upper-limit number of individuals in the environment.
Also, as the number of individuals approaches the limit, the value of the coefficient \(m\), which represents the rate of increase of individuals, should decrease. In the logistic equation, this decrease was assumed to occur linearly. That is, the relationship is as shown in the diagram below
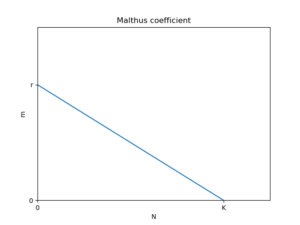
The intercept of this line represents the potential (under the extreme situation \(N\to 0\)) maximum value of \(m\) and was named the intrinsic growth rate \(r\). If we substituted the equation of the straight line
$$m=-\frac{r}{K}N+r=r\left(1-\frac{N}{K}\right)$$
into equation \((1)\), then we obtain
$$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)\tag{1*}$$
Note that the origin of the name of the logistic equation is not very clear and will not be discussed here.
Solution of the logistic equation
The logistic equation can be solved using the separation of variables method.
$$\frac{dN}{dt}=rN\left(1-\frac{N}{K}\right)$$
$$\frac{dN}{dt}=\frac{r}{K}N(K-N)$$
$$\int\frac{K}{N(K-N)}dN=r\int dt$$
Using the fact that it is decomposed into partial fractions as
$$\frac{K}{N(K-N)}=\frac{1}{N}+\frac{1}{K-N}$$
, we obtain the following relation
$$\int\left(\frac{1}{N}+\frac{1}{K-N}\right)dN=r\int dt$$
$$\ln{N}-\ln{(K-N)}=rt+C$$
$$\ln{\frac{N}{K-N}}=rt+C$$
Here, if we set \(N=N_0\) at \(t=0\) as the initial condition, then
$$C=\ln{\frac{N_0}{K-N_0}}$$
Substitute this for the solution that
$$\ln{\frac{N}{K-N}}=rt+\ln{\frac{N_0}{K-N_0}}$$
$$\ln{\frac{N(K-N_0)}{(K-N)N_0}}=rt$$
$$\frac{N(K-N_0)}{(K-N)N_0}=e^{rt}$$
$$N(K-N_0)=e^{rt}(K-N)N_0$$
$$N(K-N_0+N_0 e^{rt})=N_0 Ke^{rt}$$
$$N=\frac{N_0 Ke^{rt}}{K-N_0+N_0 e^{rt}}\tag{*}$$
Note that substituting \(K=1, N_0=0.5, r=1\) here yields
$$N=\frac{0.5e^{t}}{0.5+0.5e^{t}}$$
$$N=\frac{1}{1+e^{-t}}$$
and replacing \(N\to p\) and \(t\to a\) yields the logistic sigmoid function
$$p=\frac{1}{1+e^{-a}}$$


Comments