この記事ではAtCoderというサイトの問題を参考に、「戻す動的計画法(DP)」について解説する。
問題:ARC028 D - 注文の多い高橋商店

この問題では、「同種のものを区別せずにM個選ぶ組み合わせ」と「戻すDP」についての考察が必要となる。「同種のものを区別せずにM個選ぶ組み合わせ」の解説は前回
で行ったので、この記事を読む前に参照してほしい。そして、ここでは「戻すDP」について考えよう。これに該当する問題文は、以下の部分である。
いや、これは少し簡単過ぎるので、ちょっとした注文も追加しよう。整数 \(k, x\) からなる \(Q\) 個の注文を用意したので、それぞれについて「 \(k_{i}\) 種類目の商品をちょうど \(x_{i}\) 個選ばなければならないとき、合計 \(M\) 個の商品を選ぶ方法」の数を求めて下さい。
解説
考え方
\(N\) 番目の商品までを用いて \(M\) 個を選ぶ組み合わせについては、商品 \(A\) が \(4\) 個、 \(B\) が \(2\) 個、 \(C\) が \(3\) 個の場合、動的計画法を用いて以下のように表せることを前回示した。
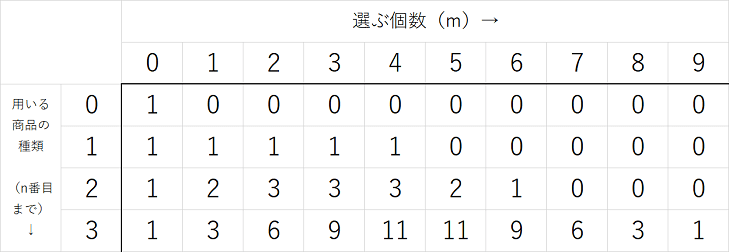
これは、商品 \(A\) が \(0\) ~ \(4\) 個、 \(B\) が \(0\) ~ \(2\) 個、 \(C\) が \(0\) ~ \(3\) 個の範囲をそれぞれ動くことができるという条件で求められたものだが、ここで再び、とある1種類については個数を限定しなくてはならなくなる。すなわち、 \(N\) 番目の商品によって加算された組み合わせの数を”元に戻す”作業が必要なのであり、このアルゴリズムのことを「戻すDP」という。
アルゴリズムの詳細
目標
さて、ここで戻すDPを使って我々が得たいものは、以下のような表である。
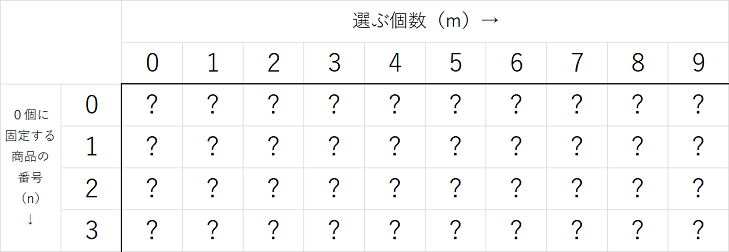
ここで、2種類の表が出てきてややこしいので、前回の動的計画法によって得られた表を行列 \(dp\) 、今回これから戻るDPによって作成する表を行列 \(rdp\) として捉え、それぞれの \(i\) 行 \(j\) 列成分を \(dp_{ij}, rdp_{ij}\) と表すことにする。
そして、上の表を得たい理由は、「 \(n\) 番目の商品の数を \(k\) 個に固定したときに、全 \(N\) 種類の商品から \(M\) 個を選ぶ組み合わせの数」が \(rdp_{n, M-k}\) に等しいからである。上記の設定を用いると、例えば「 \(A\) の個数を \(2\) 個に固定したときに、全 \(3\) 種類の商品 \(A, B, C\) から \(5\) 個を選ぶ組み合わせの数」は、「 \(A\) の個数を \(0\) 個に固定したときに、全 \(3\) 種類の商品 \(A, B, C\) から \(5-2=3\) 個を選ぶ組み合わせの数」に等しいことを確認されたい。
漸化式
戻すDPにおいても通常の動的計画法と同様に漸化式の考え方を用いる。ここでは、「最後に \(n\) 番目の商品による組み合わせを加算して、全 \(N\) 種類の商品による組み合わせの数が求まった」と考えて、「全 \(N\) 種類の商品による組み合わせの数」、すなわち \(dp\) の最終行の値を用いて、 \(rdp\) の \(n\) 行目の値についての式を立てる。
前提条件として、前回求めた \(dp\) を計算するためのルール(漸化式)を再掲する。なお、ここでは前回 \(b_{n,m}\) とおいていた「 \(n\) 番目の商品までの中から \(m\) 個選ぶ組み合わせの数」を \(dp_{n,m}\) で置き換えている。
\(m<=a_{n}\) のとき
$$dp_{n,m} = \sum_{k=0}^{M}dp_{n-1,k} \tag{1}$$\(m>a_{n}\) のとき
$$dp_{n,m} = \sum_{k=0}^{m}dp_{n-1,k}-\sum_{k=0}^{m-a_{n}-1}dp_{n-1,k} \tag{2}$$
ここで、「最後に \(n\) 番目の商品による組み合わせを加算する前の、 \(m\) 個選ぶ組み合わせの数」、すなわち、「 \(n\) 番目の商品を \(1\) つも選んでいない( \(0\) 個に固定されている)ときの、 \(m\) 個選ぶ組み合わせの数」が \(rdp_{n,m}\) で表されることを考えると、より一般的な式である \((2)\) 式を用いて
が成り立つ。なぜならば、前述の通り \(n\) 番目の商品を最後に加えたと考えるなら、 \(N-1\) 種類の商品は \(\{1, 2, ... , n-1, n+1, ... , N\}\) 番目の商品によって構成されるため、 \(dp_{N-1,k}=rdp_{n,k}\) が成り立つからである。
同様に、 \((2)\) 式を用いて添字をずらした式である
が得られ、 \((3), (4)\) 式の辺々を引くと
となり、これを並び替えると
より、 \(rdp_{n,m}\) についての漸化式が得られる。以上の結果を変数の定義域を踏まえて一般化すると
\(m<=a_{n}\) のとき
$$rdp_{n,m} = dp_{N,m}-dp_{N,m-1}$$\(m>a_{n}\) のとき
$$rdp_{n,m} = rdp_{n,m-a_{n}-1}+dp_{N,m}-dp_{N,m-1}$$
となる。したがって、通常の動的計画法によって前もって \(dp\) の最終行 \(dp_{N,.}\) の値を求めておくことで、上記のルールに従って \(rdp\) を埋めていけばよいことがわかる。
以上のように、一度通常の動的計画法により求めた値から”1歩前の状況に戻す”アルゴリズムのことを戻すDPという。
実装
前編・後編の結果をC++で実装すると以下のようになる。
通常の動的計画法で用いる \(\sum_{k=0}^{m}dp_{n-1,k}\) は、各 \(n\) において累積和 \(accum[m]\) として先に計算しておくと便利であり、かつ高速化できる。
そして、 \(rdp\) を求めた後は、入力 \(k_{i}, x_{i}\) に対して \(rdp[k][M-x]\) を解答とすればよい(理由については「解説」―「アルゴリズムの詳細」―「目標」を参照)。ただし、出力は解答を \(10^{9}+7\) で割った余りとする必要があるので、 \(dp\) や \(rdp\) を更新する都度、余りを求めておくとよい。このとき、減算( \(accum[m] - accum[m-a[n]-1]\) など)の結果は負になりうるので、適宜符号を正にしてから余りを計算する(MOD関数を作る)必要がある(1敗)。
※C++では、負の数に対する余りの計算結果は負として返される(例: \(-7\ \%\ 3 = -1\) )



Comments