Both delta and star (Y) circuits are circuits with three resistors connected.
Using the Δ-Y (delta-star) conversion formula, you can calculate the combination of resistor values that make these circuits equivalent.
Read this article to understand the principle of the Delta-Y conversion formula and its proof.
Δ-Y (delta-star) conversion
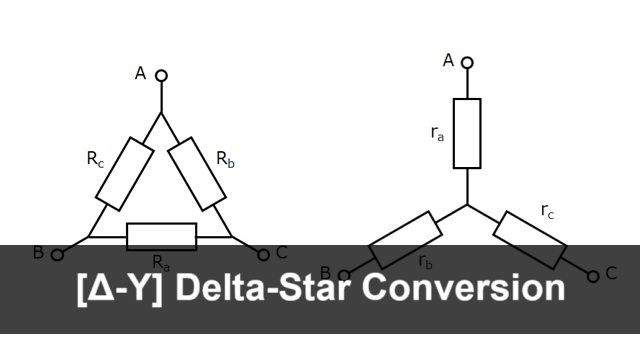
Δ circuit & Y circuit
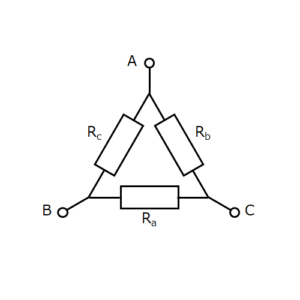
Fig. 1
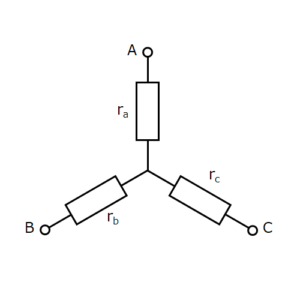
Fig. 2
Circuits such as those in Fig. 1 are called Δ (delta) circuits and those in Fig. 2 are called Y (star) circuits.
The two can be rewritten as mutually equivalent circuits.
Conversion from Δ to Y
The Δ circuit can be rewritten as a Y circuit by setting \(r_a,r_b,r_c\) as follows.
$$r_a=\frac{R_b R_c}{R_a+R_b+R_c}$$
$$r_b=\frac{R_c R_a}{R_a+R_b+R_c}$$
$$r_c=\frac{R_a R_b}{R_a+R_b+R_c}$$
In other words, the sum of the resistances of the Δ circuits is the denominator and the product of the two resistances of the Δ circuits adjacent to the resistance of the Y circuit is the numerator.
Conversion from Y to Δ
The Y circuit can be rewritten as a Δ circuit by setting \(R_a,R_b,r_R\) as follows.
$$R_a=\frac{r_a r_b+r_b r_c+r_c r_a}{r_a}$$
$$R_b=\frac{r_a r_b+r_b r_c+r_c r_a}{r_b}$$
$$R_c=\frac{r_a r_b+r_b r_c+r_c r_a}{r_c}$$
That is, the resistance of the Y circuit on the opposite side of the resistance of the Δ circuit is the denominator and the sum of the products of the adjacent resistances of the Y circuit is the numerator.
Proof
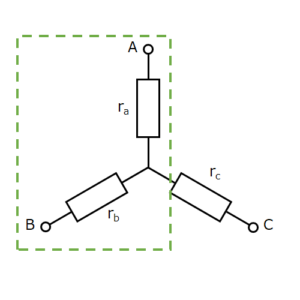
Fig. 3
If the Δ and Y circuits are equivalent, they are also equivalent if parts of them are extracted. If only the A-B connection is extracted as in Fig. 3, the corresponding part of the Δ-circuit is shown in Fig. 4 below (no special attention is paid to terminal C).
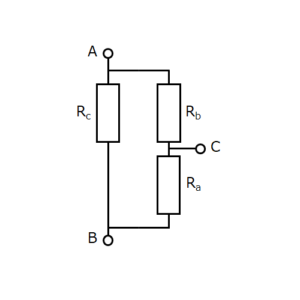
Fig. 4
Let the composite resistance of A-B in the Y circuit be \(r_a+r_b\) and the composite resistance in the Δ circuit be \(R^D_{AB}\),
$$\frac{1}{R^D_{AB}}=\frac{1}{R_c}+\frac{1}{R_a+R_b}=\frac{R_a+R_b+R_c}{R_c(R_a+R_b)}$$
then
$$R^D_{AB}=\frac{R_c(R_a+R_b)}{R_a+R_b+R_c}$$
Since these are equivalent,
$$r_a+r_b=\frac{R_c(R_a+R_b)}{R_a+R_b+R_c}\tag{1.1}$$
holds, and similarly between B-C and C-A,
$$r_b+r_c=\frac{R_a(R_b+R_c)}{R_a+R_b+R_c}\tag{1.2}$$
$$r_c+r_a=\frac{R_b(R_c+R_a)}{R_a+R_b+R_c}\tag{1.3}$$
are obtained.
If you add up these sides, then
$$2(r_a+r_b+r_c)=\frac{2(R_aR_b+R_bR_c+R_cR_a)}{R_a+R_b+R_c}$$
$$r_a+r_b+r_c=\frac{R_aR_b+R_bR_c+R_cR_a}{R_a+R_b+R_c}$$
subtracting the sides of equation \((1.1), (1.2), (1.3)\) respectively, from which
$$r_a=\frac{R_b R_c}{R_a+R_b+R_c}\tag{2.1}$$
$$r_b=\frac{R_c R_a}{R_a+R_b+R_c}\tag{2.2}$$
$$r_c=\frac{R_a R_b}{R_a+R_b+R_c}\tag{2.3}$$
is obtained.
Also, multiplying the sides of the expression \((1.3), (1.1)\) gives
$$(r_c+r_a)(r_a+r_b)=\frac{R_b(R_c+R_a)R_c(R_a+R_b)}{(R_a+R_b+R_c)^2}$$
$$r_ar_b+r_br_c+r_cr_a+r^2_a=\frac{R_bR_c(R_c+R_a)(R_a+R_b)}{(R_a+R_b+R_c)^2}$$
and dividing the sides by the expression \((2.1)\) gives
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=\frac{(R_c+R_a)(R_a+R_b)}{R_a+R_b+R_c}$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=\frac{R_a(R_a+R_b+R_c)+R_bR_c}{R_a+R_b+R_c}$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=R_a+\frac{R_bR_c}{R_a+R_b+R_c}$$
Furthermore, subtracting the sides of equation \((2.1)\), we get
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}=R_a$$
Similar calculations for the pairs of equations \((1.1)-(1.2)-(2.2), (1.2)-(1.3)-(2.3)\) lead to
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_b}=R_b$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_c}=R_c$$

Comments