 確率・統計
確率・統計【統計検定1級対策】合格のための2つの考え方と7つのステップ
筆者は2021年の統計検定1級合格者(統計数理・統計応用(医薬生物学))です。 試験勉強を始めた当初、私には統計学のバックグラウンドはほぼありませんでした。 しかし、試験問題の傾向から見えた2つの考え方を軸に対策を練り、7つのステップを達成...
 確率・統計
確率・統計 確率・統計
確率・統計 クオータニオンによる回転表現
クオータニオンによる回転表現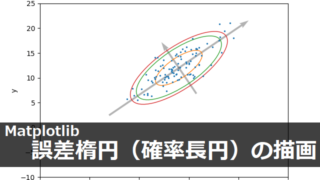 Matplotlib
Matplotlib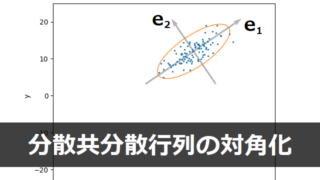 確率・統計
確率・統計 微分方程式の解法
微分方程式の解法 微分方程式の解法
微分方程式の解法 微分方程式の解法
微分方程式の解法 微分方程式の解法
微分方程式の解法 微分方程式の解法
微分方程式の解法