概要
制御工学の分野で用いられる、初期値の定理と最終値の定理について解説し、その実例と証明を示す。
定理
記号の定義
- \(f(t)\) :原関数
- \(f'(t)\) : \(f(t)\) の1回微分
- \(F(s)=\mathfrak{L}[f(t)]\) : \(f(t)\) のラプラス変換
初期値の定理
初期値 \(f(0)\) はラプラス変換を用いて次のように表せる。
$$f(0)=\lim_{s\to\infty}sF(s)$$
最終値の定理
最終値 \(f(\infty)\) はラプラス変換を用いて次のように表せる。
$$f(\infty)=\lim_{s\to 0}sF(s)$$
例
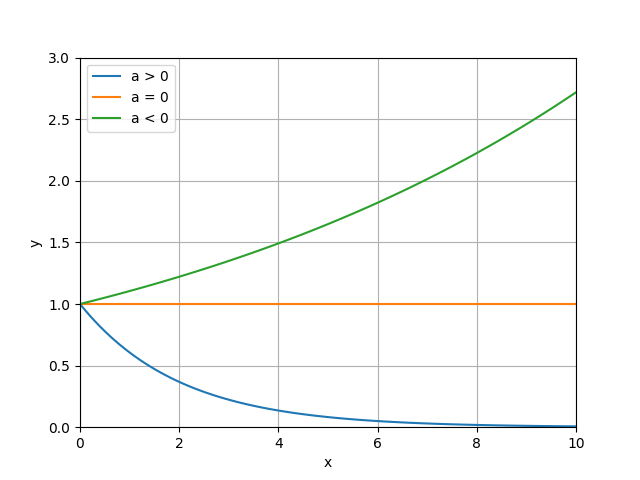
指数関数 \(f(t)=\exp{(-at)}\) を考える。
この関数のラプラス変換
$$F(s)=\frac{1}{s+a}$$
を用いて、初期値の定理より
$$f(0)=\lim_{s\to\infty}\frac{s}{s+a}=\lim_{s\to\infty}\frac{1}{1+\frac{a}{s}}=1$$
a > 0 のとき
最終値の定理より
$$f(\infty)=\lim_{s\to 0}\frac{s}{s+a}=0$$
a = 0 のとき
$$sF(s)=\frac{s}{s+0}=1$$
より、最終値の定理から
$$f(\infty)=1$$
a < 0 のとき
\(t\to\infty\) で \(f(t)\) が発散するため、最終値は存在しない。
証明
初期値の定理
原関数 \f(t)\ の1回微分のラプラス変換は
$$\mathfrak{L}[f'(t)]=\int^{\infty}_0 f'(t)\exp{(-st)}dt=sF(s)-f(0)$$
と書け、これを移項すると
$$sF(s)=\int^{\infty}_0 f'(t)\exp{(-st)}dt+f(0)\tag{1}$$
となる。
\(s\to\infty\) の極限をとると
$$\int^{\infty}_0 f'(t)\exp{(-st)}dt\to 0$$
より
$$\lim_{s\to\infty}sF(s)=f(0)$$
最終値の定理
\(s\to 0\) の極限をとると
$$\int^{\infty}_0 f'(t)\exp{(-st)}dt\to\int^{\infty}_0 f'(t)dt=[f(t)]^\infty_{0}=f(\infty)-f(0)$$
より、式 \((1)\) に代入して
$$\lim_{s\to 0}sF(s)=f(\infty)$$

Comments