デルタ回路・スター(Y)回路はともに、3つの抵抗を接続した回路です。
Δ-Y(デルタ-スター)変換の公式を用いると、これらの回路を等価にする抵抗値の組み合わせを計算できます。
この記事を読むことで、Δ-Y変換公式の原理やその証明を理解することができます。
Δ-Y(デルタ-スター)変換
Δ回路とY回路
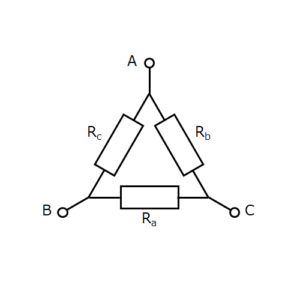
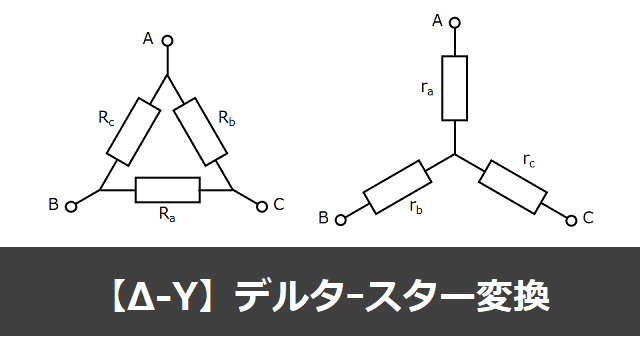
図1
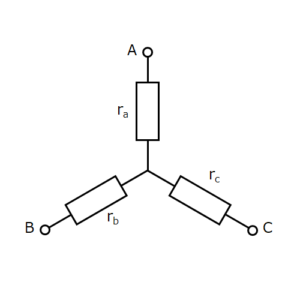
図2
図1のような回路をΔ(デルタ)回路、図2のような回路をY(スター)回路といいます。
この2つは相互に等価回路として書き換え可能です。
Δ→Yの変換
\(r_a,r_b,r_c\) を以下のように設定することで、Δ回路をY回路へと書き換えることができます。
$$r_a=\frac{R_b R_c}{R_a+R_b+R_c}$$
$$r_b=\frac{R_c R_a}{R_a+R_b+R_c}$$
$$r_c=\frac{R_a R_b}{R_a+R_b+R_c}$$
すなわち、Δ回路の抵抗の総和が分母、Y回路の抵抗に隣接するΔ回路の2抵抗の積が分子となる。
Y→Δの変換
\(R_a,R_b,R_c\) を以下のように設定することで、Y回路をΔ回路へと書き換えることができる。
$$R_a=\frac{r_a r_b+r_b r_c+r_c r_a}{r_a}$$
$$R_b=\frac{r_a r_b+r_b r_c+r_c r_a}{r_b}$$
$$R_c=\frac{r_a r_b+r_b r_c+r_c r_a}{r_c}$$
すなわち、Δ回路の抵抗の対辺にあるY回路の抵抗が分母、Y回路の隣接する抵抗の積の和が分子になります。
証明
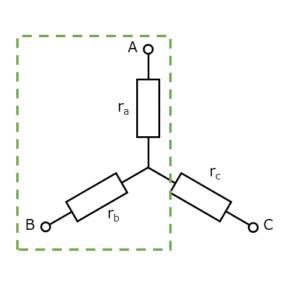
図3
Δ回路とY回路が等価である場合、その一部を取り出しても等価になります。
図3のようにA-Bの接続のみを抜き出すと、対応するΔ回路の部分は次の図4のようになります(端子Cには特に注目しない)。
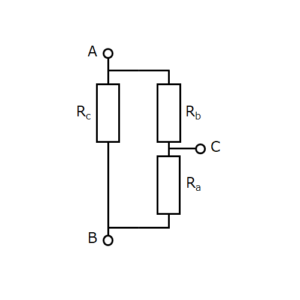
図4
Y回路におけるA-Bの合成抵抗は \(r_a+r_b\) であり、Δ回路における合成抵抗を \(R^D_{AB}\) とおくと、
$$\frac{1}{R^D_{AB}}=\frac{1}{R_c}+\frac{1}{R_a+R_b}=\frac{R_a+R_b+R_c}{R_c(R_a+R_b)}$$
より
$$R^D_{AB}=\frac{R_c(R_a+R_b)}{R_a+R_b+R_c}$$
となります。これらが等価であるので
$$r_a+r_b=\frac{R_c(R_a+R_b)}{R_a+R_b+R_c}\tag{1.1}$$
が成り立ち、またB-C, C-A間でも同様にして
$$r_b+r_c=\frac{R_a(R_b+R_c)}{R_a+R_b+R_c}\tag{1.2}$$
$$r_c+r_a=\frac{R_b(R_c+R_a)}{R_a+R_b+R_c}\tag{1.3}$$
が得られます。これらの辺々を足すと
$$2(r_a+r_b+r_c)=\frac{2(R_aR_b+R_bR_c+R_cR_a)}{R_a+R_b+R_c}$$
$$r_a+r_b+r_c=\frac{R_aR_b+R_bR_c+R_cR_a}{R_a+R_b+R_c}$$
となり、ここから式 \((1.1), (1.2), (1.3)\) の辺々をそれぞれ引くことで
$$r_a=\frac{R_b R_c}{R_a+R_b+R_c}\tag{2.1}$$
$$r_b=\frac{R_c R_a}{R_a+R_b+R_c}\tag{2.2}$$
$$r_c=\frac{R_a R_b}{R_a+R_b+R_c}\tag{2.3}$$
が求まります。
また、式 \((1.3), (1.1)\) の辺々を掛けると
$$(r_c+r_a)(r_a+r_b)=\frac{R_b(R_c+R_a)R_c(R_a+R_b)}{(R_a+R_b+R_c)^2}$$
$$r_ar_b+r_br_c+r_cr_a+r^2_a=\frac{R_bR_c(R_c+R_a)(R_a+R_b)}{(R_a+R_b+R_c)^2}$$
となり、式 \((2.1)\) で辺々を割ると
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=\frac{(R_c+R_a)(R_a+R_b)}{R_a+R_b+R_c}$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=\frac{R_a(R_a+R_b+R_c)+R_bR_c}{R_a+R_b+R_c}$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}+r_a=R_a+\frac{R_bR_c}{R_a+R_b+R_c}$$
さらに式 \((2.1)\) の辺々を引くと
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_a}=R_a$$
が求まります。
式 \((1.1)-(1.2)-(2.2), (1.2)-(1.3)-(2.3)\) の組についても同様の計算を行うと
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_b}=R_b$$
$$\frac{r_ar_b+r_br_c+r_cr_a}{r_c}=R_c$$
が導出されます。

Comments