概要
この記事では、
- 01-Kendall 順位相関係数
- 2 値 Kendall 順位相関係数
- Binary Kendall 順位相関係数
などと呼ばれそうな、Kendall 順位相関係数

の特殊な場合の計算法についてまとめる。ようするに
Redman W (2019) An O(n) method of calculating Kendall correlations of spike trains. PLoS ONE 14(2): e0212190.
にて、spike trainの Kendall 順位相関係数として扱われているケースのことを扱いたいのであるが、定まった名称はなさそうなので、検索に引っかかりそうなものを列挙しておいた次第である。
そのため、この記事内では01-Kendall 順位相関係数と呼ぶことにし、最初にこの用語の定義を行う。
その後、上記論文にしたがって効率的な計算法についてまとめる。
最後に、論文の範囲を超えて、この相関係数がとる分布の効率的な計算方法について述べる。
また、Python による実装も載せる。
定義
要素数が \(N\) の2ベクトル \(X=\{X_1, X_2, \ldots X_N\}, Y=\{Y_1, Y_2, \ldots Y_N\}\) を考える。ただし、これらのすべての要素は \(0\) または \(1\) の値をとる。すなわち、任意の \(i=1,2,\ldots,N\) について
$$X_i\in\{0, 1\}, Y_i\in\{0, 1\}$$
である。この2ベクトルについて Kendall 順位相関係数を求めることを、「01-Kendall 順位相関係数の計算」と定義する。
何の役に立つか
ONとOFFで表現される時系列が2つあったとき、それらの切り替わりはどの程度連動しているのかの
指標として用いることができる。
出典の Redman et al. では、2つの神経細胞(または電極)が、それぞれスパイク活動を起こしたときを1、休止しているときを0として記録したとき、これらの活動がどの程度相関を持っているかを表現するために用いることを提唱している。
相関係数の計算
計算時間
以下の手順で計算することにより、 \(O(N^2)\) (平衡二分木を使うと \(O(N\mathrm{log}N)\))の計算量がかかるところを、 \(O(N)\) にすることができる。
(補足)要素の重複を含む場合の Kendall 順位相関係数
Kendall 順位相関係数 \(\tau\)は、2ベクトルが要素に重複を含まないことを前提としているが、重複する要素が存在する場合は以下のように定義することができる。
$$\tau=\frac{K^+-K^-}{\sqrt{n_0-n_1}\sqrt{n_0-n_2}}$$
ここで、\(K^+, K^-\) はそれぞれconcordant pair, discordant pair(ただし、\(X_i=X_j\) または \(Y_i=Y_j\) となる組は無視する)の数であり、その他
$$n_0=\frac{N(N+1)}{2}$$
$$n_1=\frac{1}{2}\sum_i t_i (t_i-1)$$
$$n_2=\frac{1}{2}\sum_ju_j(u_j-1)$$
が成り立つ。ここで、\(t_i, u_j\) はそれぞれ、 \(X, Y\) がそれぞれ持つ \(i, j\) 番目の重複要素の個数である。例えば今回、
$$X=\{0, 1, 1, 0, 0\}$$
の場合、\(t_0=3, t_1=2\) である。
\(\tau\) の計算
\(|A|\) が集合 \(A\) の要素数を表すとし、次のように計算する。
$$A=\{i|X_i+Y_i=2\}$$
$$S=\{i|X_i+Y_i=0\}$$
$$\Delta X=\{i|X_i-Y_i=1\}$$
$$\Delta Y=\{i|X_i-Y_i=-1\}$$
$$K^+=|A|\cdot|S|$$
$$K^-=|\Delta X|\cdot|\Delta Y|$$
$$n_{1}=\frac{1}{2}\left\{\sum_{i=1}^N X_i(\sum_{i=1}^N X_i-1)+(N-\sum_{i=1}^N X_i)(N-\sum_{i=1}^N X_i-1)\right\}$$
$$n_{2}=\frac{1}{2}\left\{\sum_{i=1}^N Y_i(\sum_{i=1}^N Y_i-1)+(N-\sum_{i=1}^N Y_i)(N-\sum_{i=1}^N Y_i-1)\right\}$$
以上の計算量は、前述のとおり \(O(N)\) である。
相関係数の分布の計算
以下では Redman et al. の内容を出て、01-Kendall 相関係数の値がとる分布について考える。
(補足)要素の重複を含む場合の Kendall 順位相関係数
要素の重複を持つベクトルについて Kendall 順位相関係数を考える場合、以下の量は標準正規分布にしたがう。
$$z_B=\frac{K^+-K^-}{\sqrt{v}}$$
ただし、
$$v=\frac{v_0-v_t-v_u}{18}+v_1+v_2$$
$$v_0=N(N-1)(2N+5)$$
$$v_t=\sum_i t_i(t_i-1)(2t_i+5)$$
$$v_u=\sum_j u_j(u_j-1)(2u_j+5)$$
$$v_1=\frac{\sum_i t_i(t_i-1)\sum_j u_j(u_j-1)}{2N(N-1)}$$
$$v_2=\frac{\sum_i t_i(t_i-1)(t_i-2)\sum_j u_j(u_j-1)(u_j-2)}{9N(N-1)(N-2)}$$
である。
\(z_B\) の計算
ここでも、\(\tau\) の計算のときと同様に、
$$t_1=\sum_{i=1}^{N}X_i$$
$$t_0=N-\sum_{i=1}^{N}X_i$$
が成り立つ。 \(u_j\) についても同様である。この総和は何度も用いることになるので、一度計算したものを使い回すことで計算時間を短縮できる。
実装
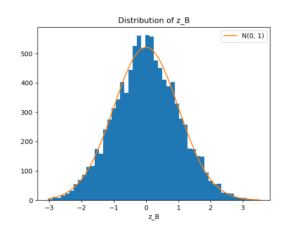
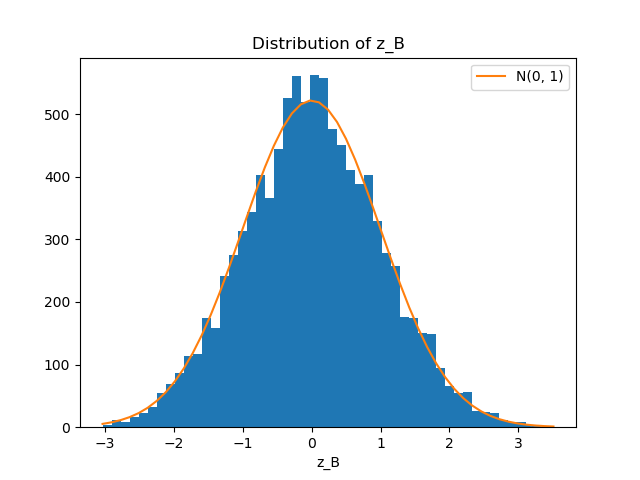
\(z_B\) が標準正規分布にしたがっていることが確認できる。
通常、Python で \(O(N^2)\) の計算を1万回転すると相当な時間がかかるが、下記のコードは数秒で終了する。

Comments